Первый закон Ньютона. ИСО

До сих пор мы изучали движение тел только кинематически. То есть мы определяли основные кинематические характеристики движения — скорость, ускорение, перемещение, и координату тела, а также устанавливали их взаимосвязь.

Уравнения кинематики позволяют решать сложные задачи движения различных частей машин и механизмов, рассчитывать траектории движущихся тел. Однако кинематика может только описать движение, пользуясь заданными наперёд его характеристиками (скоростью, ускорением), но не отвечает на вопрос о причинах возникновения движения, изменения скорости и возникновения ускорения. Изучением этих причин занимается другой раздел механики, который называется динамикой.

Вопрос о причинах, вызывающих движение различных тел, его изменение со временем, является главным не только в механике и физике, но и в нашем мировоззрении вообще.

На первый взгляд повседневный опыт просто отвечает на вопрос о причинах движения тела. Чтобы передвигать тележку с постоянной скоростью по горизонтальной дороге, необходимо приложить определённое усилие. Перестали толкать тележку — она остановилась, начали опять толкать — она вновь пришла в движение.

На основании подобных наблюдений Аристотель сформулировал общий принцип: «природа боится пустоты», то есть все пространство вокруг заполнено материей, которая препятствует или оказывает сопротивление всякому движению тела. Отсюда он пришёл к выводу, что для движения тела с постоянной скоростью необходимо приложить силу. Прекращается действие силы — прекращается движение. Поскольку Аристотель пользовался авторитетом, то это неправильное понимание причин движения являлось основной догмой механики в течение почти 2 тыс. лет.

Только в 16 веке итальянский учёный Галилео Галилей впервые на основе проведения физических опытов экспериментально доказал несостоятельность утверждений Аристотеля. Он показал, что под действием постоянной силы любое свободное тело движется не равномерно, а равноускоренно и что «любая скорость, сообщённая телу, устойчиво сохраняется до тех пор, пока нет причин к возникновению торможения или ускорения».

В отличие от Аристотеля Галилей утверждал, что тело сопротивляется не движению с постоянной скоростью, а ускорению, т. е, изменению этой скорости. При этом он понимал, что причинами возникновения торможения или ускорения тела могут быть только взаимодействия данного тела с другими телами.

Проведём опыт, подобный опытам Галилея. Возьмём твёрдый полированный шарик и будем спускать его с горки с одной и той же высоты. Под горкой горизонтально установим жёлоб в первом случае заполненный песком, во втором случае — обклеенный ворсистой тканью и в третьем случае изготовленный из полированного стекла.

В первом случае шарик, попав в песок, быстро останавливается и оставляет в песке заметный след. Во втором случае скорость изменяется заметно меньше и шарик перемещается немного дальше. В третьем случае шарик будет двигаться до конца желоба почти с постоянной скоростью.

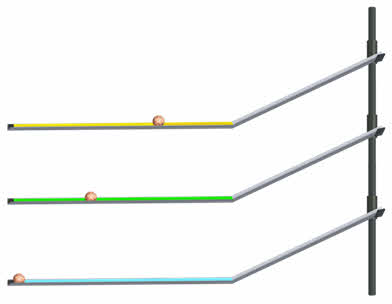
Движение тела, которое происходит без действия на него других тел, называют движением по инерции.

Таким образом, инерция — это явление сохранения скорости тела при отсутствии действия на него других тел.

А свойство тел, проявляющееся в том, что скорость их движения остаётся неизменной до тех пор, пока на них не действуют другие тела, называется инертностью.

Анализ результатов опытов позволил Галилею сформулировать закон инерции: скорость движения тела остаётся постоянной, если на него не действуют другие тела или их действия компенсируются.

Обобщив и уточнив результаты работ Галилея, английский учёный Исаак Ньютон в своём труде «Математические начала натуральной философии» включил закон инерции в число основных аксиом движения. Поэтому закон инерции часто называют первым законом Ньютона.

В нём утверждается, что: существуют такие системы отсчёта, в которых тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока на него не подействуют другие тела или действия других тел компенсируются.

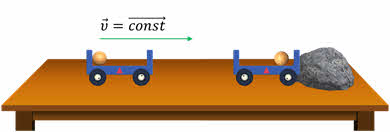
Таким образом, в первом законе Ньютона постулируется существование таких систем отсчёта, в которых выполняется закон инерции. Они получили название инерциальных систем отсчёта (сокращённо ИСО).

Значит, ИСО — это такие системы отсчёта, относительно которых тело при компенсации внешних воздействий движется прямолинейно и равномерно.

Доказать теоретически первый закон Ньютона невозможно; его следует рассматривать как результат обобщения экспериментальных фактов. Но как установить, что какая-либо система отсчёта является инерциальной?

Это можно сделать только на основе эксперимента. Проведём опыт. Тележку с находящимся на ней игрушечным автомобилем будем двигать равномерно и прямолинейно. В системе отсчёта, связанной с тележкой, автомобиль покоится, относительно Земли — движется с постоянной скоростью, равной скорости тележки. Следовательно, с тележкой можно связать инерциальную систему отсчёта.

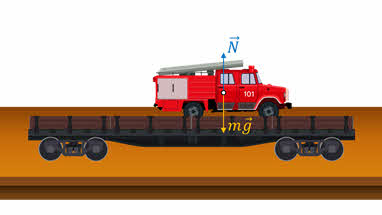
Резко ускорим движение тележки. Автомобиль покатится по тележке назад. А если резко замедлить движение тележки? Автомобиль покатится по тележке вперёд. Создаётся впечатление, что автомобиль двигала какая-то сила. Но на самом деле такой силы нет. Силы тяжести и упругости, действующие на автомобиль, компенсировали друг друга, а сила трения пренебрежимо мала. Поэтому автомобиль двигался, сохраняя неизменной свою скорость относительно Земли. Двигаясь относительно Земли равномерно, автомобиль отставал от тележки во время её разгона и опережал тележку при её торможении. Следовательно, в этом случае система отсчёта, связанная с тележкой, будет неинерциальной.

— А является ли система отсчёта, связанная с Землёй, инерциальной?

Это очень важный вопрос, потому что все эксперименты мы проводим на Земле. Вы знаете, что Земля движется вокруг Солнца почти по круговой орбите, а также вращается вокруг своей оси. Строго говоря, система отсчёта, связанная с Землёй, не является инерциальной.

Однако отличие этой системы от инерциальной будет очень малым, так как за те небольшие интервалы времени, за которые мы проводим эксперименты, дугу орбиты, по которой движется Земля, можно с большой точностью считать отрезком прямой линии. Ускорение же, возникающее из-за вращения Земли, тоже очень мало. Поэтому с точностью, необходимой для проведения наших экспериментов, мы можем считать систему отсчёта, связанную с Землёй, инерциальной.

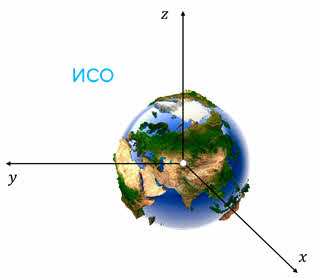
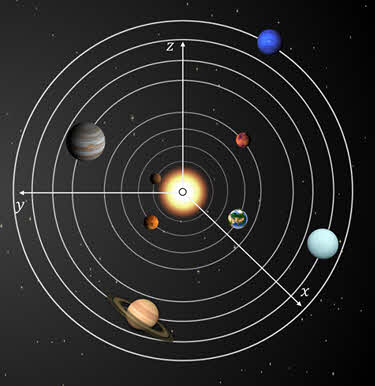
Однако, если требуется большая точность, например, при расчётах движений космических аппаратов, то инерциальной можно считать гелиоцентрическую систему отсчёта. При этом точка отсчёта совмещается с центром Солнца, а координатные оси направляются на удалённые звезды.

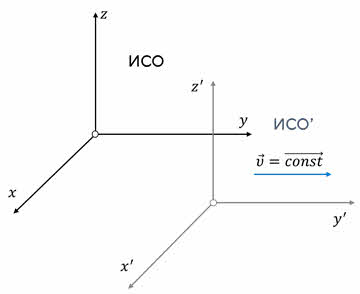
Если известна из опыта хотя бы одна инерциальная система отсчёта, то инерциальными будут любые другие системы отсчёта, движущиеся относительно избранной равномерно и прямолинейно. В этом заключается принцип равноправности инерциальных систем отсчёта.

В заключении отметим, что все законы движения и взаимодействия тел, которые мы будем изучать в дальнейшем, сформулированы для ИСО, так как в них они имеют самый простой вид. Поэтому, при решении задач вначале необходимо выбрать инерциальную систему отсчёта, и только потом применять тот или иной закон для решения.