Предмет стереометрии

Материал урока.

В курсе геометрии базовой школы, мы с вами в основном знакомились с плоскими фигурами, напомню, что раздел геометрии, который занимается изучением свойств плоских фигур называется планиметрия. Основными фигурами планиметрии являются точка и прямая. У плоских фигур есть только два измерения: длина и ширина, эти измерения используются для нахождения площади фигур.

Но мы уже знаем, что есть такой раздел геометрии, который занимается изучением объемных фигур, он называется стереометрия.

Напомним, что если в планиметрии мы говорили о квадрате, то в стереометрии мы будем говорить о кубе, который состоит из квадратов.

Если в планиметрии мы говорили о прямоугольном треугольнике, то в стереометрии из треугольника, вращая его вокруг одного из катетов, мы получим конус.

С некоторыми фигурами стереометрии мы уже знакомы: это призма, пирамида, цилиндр, конус, шар.

В курсе геометрии десятого и одиннадцатого классов, мы будем работать именно со стереометрией, то есть изучать свойства фигур в пространстве.

На прежде чем приступить к изучению стереометрии, давайте, еще раз вспомним как все начиналось.

Слово стереометрия происходит от двух древнегреческих слов «стереос» – «твердый, пространственный» и слово «метрио» – измеряю. В отличии от планиметрии основными фигурами стереометрии являются точка, прямая и плоскость.

Точки, как и в планиметрии обозначаются заглавными буквами латинского алфавита. Прямые обозначаются строчными буквами латинского алфавита.

Плоскость может изображаться разными способами, но чаще всего она изображается параллелограммом. Для обозначения плоскости используются строчные буквы греческого алфавита.

Наряду с этими понятиями в стереометрии рассматриваются геометрические тела и их поверхности. У геометрических тел три измерения: длина, ширина и высота. Эти измерения позволяют вычислить объем фигуры, то есть геометрические тело обладают вместимостью. Практически каждый окружающий нас предмет можно представить в виде геометрических тел.

Стереометрия, как и планиметрия, возникла и развивалась вместе с человеком. Геометрия была очень нужна строителям, которые возводили на реках дамбы, перекидывали с одного берега на другой мосты, виадуки, создавали многоэтажные здания и величественные храмы.

Ярким примером этого являются египетские пирамиды, сооруженные за два четыре тысячелетия до нашей эры. До сих пор эти пирамиды поражают точностью своих метрических соотношений.

Считается, что геометрия появилась в древнем Египте около 2000 лет до нашей эры.

Сначала геометрия была интуитивной. То есть факты признавались существующими и никак не доказывались. Но в 600 году до нашей эры греческий ученый Фалес выдвинул и развил идею о том, что должны быть пути, доказывающие справедливость тех или иных фактов. В геометрии факты называются теоремами. Фалес открыл доказательства теорем, которые люди принимали на веру до этого.

Начиная с VIIвека до нашей эры в Древней Греции создаются философские школы, в которых происходит постепенный переход от практической к теоретической геометрии.

Одной из самых первых и самых известных геометрических школ была пифагорейская, она существовала в VI-V веках до нашей эры. Названа она была в честь своего основателя древнегреческого ученого Пифагора.

Пифагорейцы использовали правильные многогранники для философских теорий. Так огню они придавали форму тетраэдра (пирамиды), земле – форму гексаэдра (куба), воздуху – форму октаэдра (фигуры, которая образована восьмью равносторонними треугольниками), воде – форму икосаэдра (фигуры, которая образована двадцатью равносторонними треугольниками).

По их мнению, вся вселенная имеет форму додекаэдра (фигуры, которая состоит из двенадцати правильных пятиугольников).

Нетрудно заметить, что названия многогранников тоже имеют древнегреческое происхождение. Первая часть названия показывает количество граней из которых состоит фигура, а слово «эдр» произошло от древнегреческого слова «эдра» – грань.

Еще одной известной школой, которая занималась вопросами геометрии, является Александрийская философская школа. Выходцем этой школы был знаменитый ученый Евклид, который жил около 300 года до нашей эры.

Евклид является автором «Начала», работы, которая состоит из тринадцати книг и содержит изложение планиметрии, стереометрии, ряда вопросов теории чисел. Этой работой Евклид создал фундамент дальнейшего развития математики. До сих пор этот труд считается основой изучения курса геометрии.

Он сформулировал пять постулатов:

1.  Через две точки можно провести прямую.

2.  Отрезок прямой можно продолжить неограниченно.

3.  Из всякого центра любым расстоянием можно описать окружность.

4.  Все прямые углы равны между собой.

5.  Всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними внутренние односторонние углы, сумма которых меньше 2-х прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше 2-х прямых.

В девятнадцатом веке в геометрии появились новые методы, которые позволили переводить геометрические задачи на язык алгебры и наоборот. Возникли и развиваются новые направления геометрических исследований: геометрия Лобачевского, проективная геометрия, топология, компьютерная геометрия и так далее.

В 1829 году русский математик Николай Лобачевский написал работу «О началах геометрии», в которой заявил, что можно построить геометрию такую же содержательную и свободную от противоречий, как и евклидова.

Если геометрию Евклида можно назвать геометрией земных пространств и расстояний, то геометрия Лобачевского – геометрия гигантских межпланетных и исчезающих малых атомных пространств, она включает геометрию Евклида как составную часть, как частный случай. Основное отличие геометрии Лобачевского от геометрии Евклида заключается в так называемом «пятом постулате». Евклид утверждал, что «Через точку, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её». В геометрии Лобачевского вместо этой аксиомы принимается другая аксиома: «Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её».

В 1899 году немецкий математик Давид Гильберт написал труд «Основания геометрии». Эта работа стала образцом для дальнейших работ по аксиоматическому построению геометрии.

Но математикой в целом и геометрией в частности интересовались не только ученые. Существует так называемое математическое искусство Эшера.

Голландский художник Мориц Корнилис Эшер, родившийся в 1898 году в Леувардене создал уникальные и очаровательные работы, в которых использованы или показаны широкий круг математических идей.

Правильные геометрические тела — многогранники — имели особое очарование для Эшера. Во его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов.

 Существует лишь пять правильных многогранников, то есть таких тел, все грани которых состоят из одинаковых правильных многоугольников. Они еще называются телами Платона. Это — тетраэдр, гранями которого являются четыре правильных треугольника, куб с шестью квадратными гранями, октаэдр, имеющий восемь треугольных граней, додекаэдр, гранями которого являются двенадцать правильных пятиугольников, и икосаэдр с двадцатью треугольными гранями.

На гравюре «Четыре тела» Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.

Вернемся к геометрическим телам. Геометрические тела, как и все геометрические фигуры являются воображаемыми объектами.

Геометрическое тело – часть пространства, отделенное от остальной части пространства границей этого тела.

Все геометрические тела делятся на два больших класса: тела вращения (из названия понятно, что к ним относятся тела, которые получаются вращением плоских фигур вокруг одного из своего элемента) к ним относятся шар (получается вращением полукруга вокруг диаметра), цилиндр (получается вращением прямоугольника вокруг одной из своих сторон), конус (получается вращением прямоугольного треугольника вокруг одного из своих катетов).

Ко второй группе геометрических тел, относятся многогранники – тела, ограниченные конечным числом плоских многоугольников, любые два смежные из которых не лежат в одной плоскости.

Многогранники в свою очередь делятся на призмы (это многогранник, у которого две грани – равные n-угольники, а остальные n граней – параллелограммы), пирамиды (многогранник, составленный из n угольника А₁А₂ и так далее А_n и n треугольников). С некоторыми видами многогранниками, мы с вами уже встречались, с остальными познакомимся в этом году.

Напомним, что многогранники бывают выпуклыми (то есть многогранник расположен по одну сторону от плоскости каждой его грани). Мы помним, что все грани выпуклого многогранника являются выпуклыми многоугольниками.

И невыпуклыми, когда многогранник лежит по разные стороны хотя бы от одной плоскости, проходящей через грань.

Давайте повторим основные элементы фигур, с которыми мы уже знакомы.

Начнем с тел вращения. У цилиндра есть ось, высота, основания цилиндра, радиус цилиндра, боковая или цилиндрическая поверхность, образующая.

У конуса также есть ось, высота, основание, радиус, коническая или боковая поверхность, образующая.

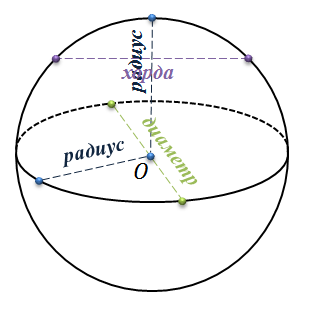
У шара или сферы (напомним, что сфера – оболочка шара, по аналогии с окружностью и кругом в планиметрии) есть центр, радиус, хорда, диаметр.

Теперь рассмотрим многогранники.

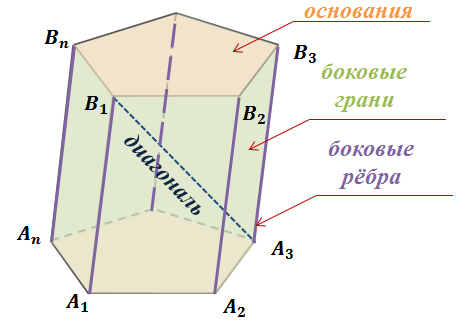
Призма имеет два основания, боковые грани, боковые ребра, у призмы есть диагональ – отрезок соединяющий две вершины призмы, не принадлежащие одной грани.

У пирамиды, в отличии от призмы – одно основание, есть боковые грани, вершина, боковые ребра, высота.

Закончить наш сегодняшний урок хочется цитатой Галилео Галилея «Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать».