Вопросы занятия:
· повторить, какие числа входят в множество натуральных чисел;
· повторить классы и разряды натуральных чисел;
· повторить правила округления и сравнения натуральных чисел;
· повторить порядок выполнения действий над натуральными числами;
· повторить понятия делителя и кратного, основные признаки делимости;
· повторить алгоритмы вычисления наименьшего общего кратного и наибольшего общего делителя.
Материал урока
Ещё в самом раннем возрасте вы впервые познакомились с числами. Это были числа, которые можно использовать для счёта. Множество таких чисел называют множеством натуральных чисел.
Обратите внимание на то, что число 0 не входит в это множество.
Начиная со второго, каждое число натурального ряда на единицу больше предыдущего. Не трудно заметить, что этот ряд бесконечен. Причём есть наименьшее число, оно равно единице, а вот наибольшего числа нет.
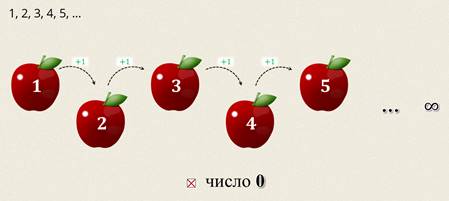
Понятно, что с ростом чисел будут получаться двузначные, трёхзначные и так далее.
Сейчас напомним классы и разряды натуральных чисел.
Рассмотрим такое число. Объединим цифры этого числа в тройки, начиная с конца. Так мы выделили классы числа. Крайний справа — класс единиц, далее — класс тысяч, класс миллионов и класс миллиардов.
К слову названия классов можно и продолжить: триллионы, квадриллионы, квинтиллионы, секстиллионы и септиллионы. Но на практике с такими большими числами мы не сталкиваемся, поэтому запоминать их названия не имеет никакого смысла.

Интересно то, что самое большое число назвать нельзя, но представить возможно. Сосчитав примерное количество частиц известной нам Вселенной, ученые показали, что оно представляет собой единицу с нулями в количестве от семидесяти девяти до восьмидесяти двух. Оно однозначно меньше единицы с сотней нулей. А вот это число имеет неофициальное название гугол. Оно то и позволит вам представить невообразимо большое число.

Вернёмся к нашему одиннадцатизначному числу. Чтобы прочитать его, поочерёдно будем называть числа, записанные в классах.
В данном случае это 13 миллиардов 946 миллионов 701 тысяча и 325 единиц.
Каждый класс имеет 3 разряда: разряд единиц, разряд десятков и разряд сотен.
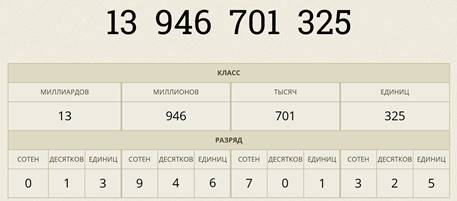
Стоит напомнить, что числа 1, 10, 100 и так далее называются разрядными единицами.
С их помощью любое натуральное число можно записать в виде суммы разрядных слагаемых.
Пример.

А сейчас поговорим об округлении натуральных чисел. Округлять натуральные числа можно до десятков, сотен, тысяч и так далее.
Повторим правило округления на конкретных примерах.
Пример.

Далее давайте вспомним правила сравнение натуральных чисел.
Для этого могут быть использованы знаки больше, меньше либо равно.

Пример.

Выражения, полученные в первых четырёх случаях, называют числовыми неравенствами.
А выражения, содержащие знак равно, называют числовыми равенствами.

Далее вспомним, какие действия можно выполнять над натуральными числами.



Пример.

Пример.

Напомним, что:


Вспомним определения делителя и кратного.

Среди всех натуральных чисел выделяют простые и составные.
Определение.
Простыми называют натуральные числа, которые делятся на единицу и на само себя.
Приведём примеры простых чисел: 2, 3, 5, 7, 11, 13, 17, 19 и т.д.
Стоит отметить, что среди простых чисел есть только одно чётное — это число 2. И существует таблица простых чисел.
Все остальные числа называют составными. Они имеют более двух делителей.
Обратите внимание, что число 1 не относится ни к одной из групп. Ведь оно имеет только один делитель.
И вам уже известны некоторые признаки делимости, которые относительно быстро позволяют определять, является ли данное число кратным тому или иному.
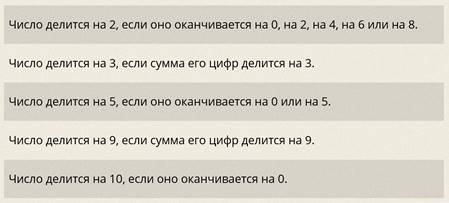
Пример.

Понятно, что многие числа имеют общие кратные и общие делители, и часто при решении задач нужно находить наименьшее общее кратное (НОК) и наибольший общий делитель (НОД) двух и более чисел. Вспомним алгоритмы, которые помогут это сделать.
Но для начала напомним, как можно разложить число на простые множители.

Пример.
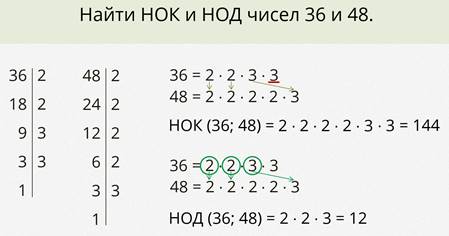
Пример.

Итоги урока
Вот так мы с вами повторили все о натуральных числах.
А именно: какие числа входят в множество N натуральных чисел; классы и разряды натуральных чисел; правила их округления и сравнения; а также порядок выполнения действий над натуральными числами. Мы вспомнили понятия делителя и кратного, повторили основные признаки делимости и алгоритмы вычисления наименьшего общего кратного и наибольшего общего делителя.


 Получите свидетельство
Получите свидетельство Вход
Вход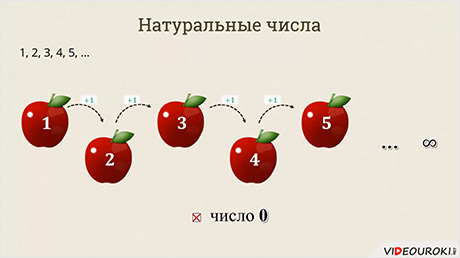



 0
0 8432
8432

