Числовые функции. Определение и способы задания

Вопросы занятия:

·     повторить определение числовых функций;

·     повторить способы задания функций;

·     повторить основные преобразования графиков числовых функций;

·     повторить вид графиков основных функций.

Материал урока

Определение.

Если даны числовое множество X и правило f, которое позволяет поставить в соответствие каждому элементу x из множества X определенное число y, то говорят, что задана функция y=f(x) с областью определения X.

Область определения обозначается D(f).

x – независимая переменная или аргумент.

y – зависимая переменная.

Множество всех значений y=f(x), где x принадлежит множеству X называют областью значений функции и обозначают E(f).

Определение.

Если дана функция y=f(x), где x принадлежит множеству X и на координатной плоскости  отмечены все точки вида (x, y), где x принадлежит множеству X, а y=f(x), то множество этих точек называют графиком функции y=f(x), где x принадлежит множеству X.

Перед вами графики некоторых функций и их названия.

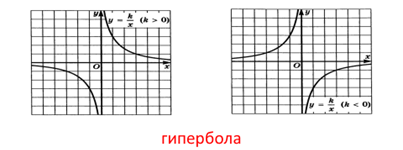
Зная график функции f(x) с помощью геометрических преобразований можно построить график функции y=f(x+a)+b. Для этого надо сделать параллельный перенос графика функции f(x) на вектор (-a;b), то есть на │a│ вправо, если a<0, и влево, если a>0 на │b│ вверх, если b>0, и вниз, если b<0.

Пример.

Определение.

Задать функцию – указать правило, которое позволяет по произвольно выбранному значению x из области определения функции вычислить соответствующее значение y.

Способы задания функции.

Чаще всего это правило связано с формулой (например, y=3x+5). Такой способ задания функции называется аналитическим.

Пример.

Тем самым на отрезке [a; b] задана функция y=f(x). Такой способ задания функции называют графическим.

Заметим, что если функция была задана аналитически и нам удалось построить ее график, то тем самым мы фактически осуществили переход от аналитического способа задания функции к графическому.

Табличный способ задания функции – с помощью таблицы, в которой указаны значения функции для конечного множества значений аргумента.

Например:

Словесный способ задания функции – способ, при котором правило задания функции описывается словами.

Пример.