Гармонические колебания

Теперь зная, как связаны между собой ускорение и координата колеблющегося тела, можно найти зависимость координаты от времени. Для этого давайте с вами рассмотрим равномерное вращение материальной точки по окружности известного радиуса. Пусть рассматриваемое движение происходит против хода часовой стрелки. Выберем систему координат ХОY так, как это показано на рисунке.

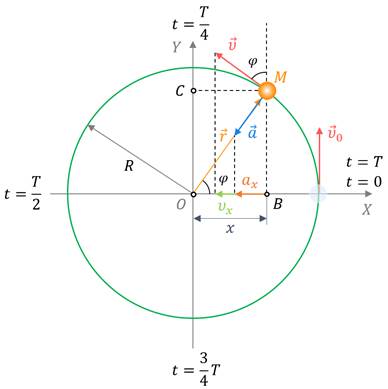
Теперь предположим, что через некоторый промежуток времени Δt материальная точка повернулась на угол φ. Давайте вспомним, что придвижении по окружности материальная точка обладает линейной скоростью, направленной по касательной в каждой точке траектории, и центростремительным ускорением, направленным всегда по радиусу к центру окружности. Спроецируем на ось OX радиус-вектор движущейся точки, её линейную скорость и центростремительное ускорение.

Проекция радиус-вектора в положении «Эм» (М) (это точка В) является смещением материальной точки от центра окружности вдоль оси Ох. Следовательно, на выбранной оси этому смещению соответствует координата х точки В.

Поскольку при равномерном вращении точки по окружности её координата (смещение) будет периодически изменяться от x_min = –R до х_max = +R, то можно сказать, что точка В совершает колебательное движение вдоль оси Ох, а её координата х является координатой колеблющейся точки.

Соответственно будут изменяться и проекция линейной скорости (от +υ₀ = ωR до –υ₀ = –ωR) и проекция центростремительного ускорения материальной точки (от +a₀ = ω²R до –a₀ = ω²R).

Теперь вспомним, что угол поворота материальной точки при её движении по окружности можно найти, как произведение угловой скорости точки и времени поворота:

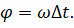
Так как при равномерном вращении по окружности линейная скорость направлена по касательной, а центростремительное ускорение — к центру окружности, то изменение координаты, проекции скорости и центростремительного ускорения материальной точки будут описываться уравнениями, которые вы сейчас видите на экране:

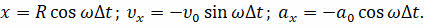
Перепишем данные уравнения, выразив начальную скорость и ускорение точки через угловую скорость:

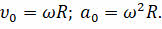
Поскольку функции синуса и косинуса являются периодическими, то через промежуток времени, равный периоду, все характеристики движения точки В вдоль оси Ох примут прежние значения, то есть значения характеристик периодически повторяются. А как мы говорили на прошлом уроке, повторяемость — это основной признак периодического движения.

Обратим внимание на то, что проекция ускорения точки B в любой момент времени пропорционально смещению и противоположно ей по знаку:

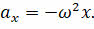
Перепишем это равенство так, как это показано на экране:

Колебания, описываемые полученным уравнением, называются гармоническими, а система, совершающая такие колебания, — гармонической колебательной системой, или гармоническим осциллятором.

Гармоническими колебаниями называются колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса:

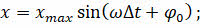
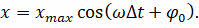
Термин «гармонические колебания» впервые был введён в науку швейцарским физиком Даниилом Бернулли.

В записанных уравнениях φ₀ — это начальная фаза колебаний, которая определяет состояние колебательной системы в начальный момент времени.

x_max — это максимальное смещение материальной точки от положения устойчивого равновесия, называемое также амплитудой колебаний:

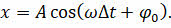
Она определяется энергией, которую сообщают точке в начальный момент времени.

ω — это циклическая частота. Она показывает, какое число полных колебаний материальная точка совершает за 2π секунд:

Наименьший промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебание, называется периодом колебаний:

А число полных колебаний, совершаемых в единицу времени, называется частотой колебаний:

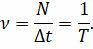
Так как в СИ единицей периода колебаний является секунда, то единицей частоты в СИ служит с^–1. Она носит название герц в честь первооткрывателя электромагнитных волн Генриха Герца.

С учётом определения периода и частоты колебаний, можно получить ещё две формулы для определения циклической частоты:

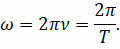
Ещё одной важной характеристикой гармонических колебаний является их фаза. Фазой колебания называется аргумент периодической функции, определяющий значение физической величины в любой момент времени. Единицей фазы в СИ является радиан.

Зависимость координаты точки от времени называется кинематическим законом (или уравнением) гармонических колебаний, поскольку позволяет определить положение точки, её скорость и ускорение в произвольный момент времени.

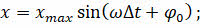
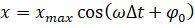
Скорость будет являться первой производной смещения по времени:

А ускорение — это первая производная скорости по времени или вторая производная смещения по времени:

Теперь давайте сравним уравнение гармонических колебаний с динамическими уравнениями математического и пружинного маятников, полученные нами на прошлом уроке:

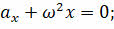
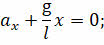
Не трудно заметить, что вот эти вот величины, являются квадратом циклической частоты маятников. Извлекая квадратный корень из этих двух выражений, найдём формулы, по которым можно рассчитать циклические частоты математического и пружинного маятников:

Учитывая, что период колебаний обратно пропорционален циклической частоте (T = 2π/ω), получим формулы для определения периода колебаний пружинного и математического маятников:

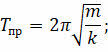
Как видно из формул, период, а, следовательно, и частота колебаний пружинного маятника не зависят от амплитуды его колебаний (в пределах выполнимости закона Гука). Он определяется лишь массой груза и жёсткостью пружины.

А период и частота математического маятника не зависят от массы маятника и амплитуды его колебаний, а определяются только его длиной и модулем ускорения свободного падения.

Кстати, впервые формулу для периода математического маятника получил ученик Исаака Ньютона Христиан Гюйгенс. Поэтому она называется формулой Гюйгенса.

Давайте с вами для примера определим амплитуду, циклическую частоту, период и начальную фазу колебаний тела массой пол килограмма, подвешенного к вертикальной пружине, если известно, что в состоянии покоя тело растягивает пружину на расстояние 5 мм и для возбуждения колебаний его смещают вниз на расстояние 20 мм от положения равновесия и отпускают.

В заключении урока отметим, что гармонические колебания полностью подчиняются закону сохранения энергия. Полная механическая энергия при гармонических колебаниях равна сумме кинетической и потенциальной энергий колебательной системы:

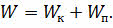
При этом, если в колеблющейся системе отсутствуют силы сопротивления, то её полная механическая энергия остаётся неизменной. Она равна либо потенциальной энергии в момент максимального отклонения от положения равновесия, либо же кинетической энергии в момент, когда тело проходит положение равновесия.