Вопросы:
· Циклические алгоритмы.
· Цикл с предусловием и принцип его работы.
· Программирование цикла с предусловием в языке Python.
В некоторых алгоритмах может потребоваться несколько раз повторить одну и ту же последовательность действий. Рассмотрим, например, алгоритм чтения книги. Для того, чтобы прочесть книгу, необходимо сначала её открыть, после чего, пока книга не закончится, нужно прочитывать по две страницы и переворачивать страницу. После окончания чтения нужно закрыть книгу. Такие алгоритмы, как описанный, называются циклическими. Они содержат циклы. Цикл – это алгоритмическая конструкция, которая представляет собой последовательность действий, повторяющихся многократно. Различают три вида циклов: цикл с заданным условием продолжения работы, который называется также циклом с предусловием; циклы с заданным условием окончания работы или с постусловием, а также циклы с параметром.
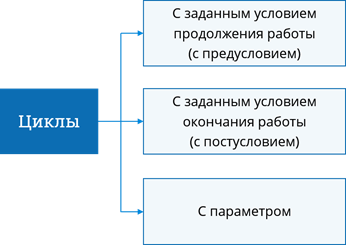
Блок-схема алгоритма чтения книги выглядит так.
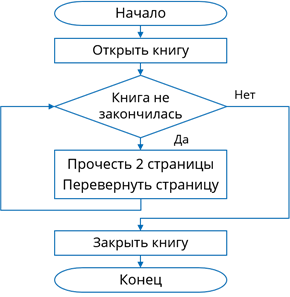
Алгоритм чтения книги содержит цикл с предусловием. Его исполнение начинается с проверки условия. Если условие выполняется, следуют некоторые действия, которые называются телом цикла. После исполнения тела цикла вновь проверяется его условие. Так продолжается до тех пор, пока условие цикла выполняется. Когда условие цикла станет ложным, цикл завершит свою работу.
Рассмотрим, как описывается цикл с предусловием на языке Python. Его описание начинается со служебного слова while, что в переводе на русский язык означает «пока». Через пробел, после него следует условие продолжения работы цикла. Оно, как и в случае с ветвлением, представляет собой выражение логического типа bool. Дальше следует двоеточие, а со следующей строки, с отступом – тело цикла, то есть инструкции, исполнение которых будет повторяться до тех пор, пока условие цикла истинно. Как и в случае с ветвлением, важно соблюдать отступы, иначе программа работать не будет. По умолчанию отступ в языке Python равен четырём пробелам, хотя интерпретатор распознает и другие пробельные отступы, важно лишь их наличие.

Рассмотрим задачу. Написать программу для вычисления суммы цифр целого числа.
Для решения задачи мы будем выделять правую цифру числа путём вычисления его остатка от деления на десять, учитывать найденную цифру при расчёте суммы, после чего убирать эту цифру из числа путём его безостаточного деления на десять. Мы будем повторять эти действия до тех пор, пока в числе не останется цифр, то есть пока оно больше нуля.
Напишем модуль для решения задачи. Вначале, с помощью инструкции print, выведем на экран сообщение о том, что это программа, вычисляющая сумму цифр целого числа, и запрос на его ввод. Дальше запишем инструкцию для считывания числа в переменную n. Так как по условию число целое – при вводе будем преобразовывать его значение в целочисленный тип int. Введённое число необязательно положительное, поэтому для вычисления суммы цифр будем использовать его модуль. Для получения модуля числа присвоим переменной n значение функции abs (n). Прежде чем начать вычисление суммы цифр числа, объявим переменную для её хранения. Назовём её s и присвоим ей значение ноль. Теперь начнём вычисление суммы цифр числа. Для этого запишем цикл while. Условием продолжения его работы будет то, что в числе n ещё остались цифры, то есть оно больше нуля. В теле цикла запишем единственную инструкцию присваивания переменным s и n соответственно s + n % 10, а также n // 10. Таким образом, на каждом шаге цикла к переменной s будет добавляться значение правой цифры n, после чего эта цифра будет убрана из числа. По завершении работы цикла, в переменной s будет храниться значение суммы цифр числа. Поэтому с помощью инструкции pritn выведем на экран сообщение о том, что сумма цифр введённого числа равна значению переменной s.
print ('Программа, вычисляющая сумму цифр целого числа. Введите число.')
n = int (input ())
n = abs (n)
s = 0
while n > 0:
s, n = s + n % 10, n // 10
print ('Сумма цифр введённого числа:', s)
Запустим модуль на выполнение и введём число 32768. Сумма его цифр действительно равна 26. Ещё раз запустим модуль и введём число -256. Сумма его цифр действительно равна 13. Программа работает правильно. Задача решена.
Ещё раз обратим внимание на принцип работы цикла с предусловием. Перед началом выполнения тела цикла проверяется его условие, поэтому если условие такого цикла изначально ложно, то тело цикла не будет выполнено ни разу. Исполнение тела цикла повторяется до тех пор, пока условие цикла истинно. Поэтому если условие цикла будет всегда истинно, то цикл будет повторяться бесконечно, то есть исполнение программы никогда не будет завершено само по себе. Оно будет завершено либо ошибкой при переполнении одной из переменных, либо его прервёт пользователь. В таких случаях говорят, что программа зациклилась. Однако и бесконечные циклы также нашли применение в некоторых языках программирования, его мы рассмотрим в следующих уроках. Заголовок наиболее простого бесконечный цикла: while True.
Рассмотрим ещё одну задачу. Написать программу, которая определяет, является ли простым введённое целое положительное число.
Простым называется целое число, которое без остатка делится только на себя и на единицу. Услышав это определение, многие из вас наверняка догадались, что для того, чтобы узнать, является ли число Эн простым, достаточно проверить его делимость на все целые числа на промежутке от двух до Эн минус один.
Напишем программу для решения задачи. Вначале, с помощью инструкции print, выведем сообщение о том, что это программа, определяющая, является ли целое положительное число простым, и запрос на ввод числа. Дальше запишем инструкцию для считывания введённого числа в переменную n. Так как по условию задачи число целое, то при вводе мы будем преобразовывать его значение в целочисленный тип int. Истинность высказывания о том, что число n – простое мы будем хранить в логической переменной p. Предположим, что n – простое число, поэтому присвоим переменной p значение «истина». Также нам понадобится переменная, в которой мы будем перебирать предполагаемые делители n. Назовём её m, присвоим ей значение наименьшего предполагаемого делителя, то есть два. Дальше запишем цикл while, для проверки того, является ли число простым. Он будет продолжать свою работу, пока значение m меньше n. В цикле запишем инструкцию ветвления с условием, что остаток от деления n на m равен нулю; если это условие выполняется, значит n не является простым числом и мы присвоим логической переменной p значение «ложь», в противном случае – ничего делать не будем. Далее, для перехода к следующему предполагаемому делителю, увеличим значение m на единицу. Таким образом, по завершении работы цикла в переменной p, будет храниться истинность высказывания о том, что n – простое число. Для вывода ответа на вопрос задачи запишем инструкцию ветвления с переменной p в качестве условия. Если переменная p имеет значение «истина», выведем на экран сообщение о том, что число n является простым, в противном случае – выведем на экран сообщение о том, что число n не является простым.
print ('Программа, определяющая, является ли целое положительное число простым. Введите число.')
n = int (input ())
p = True
m = 2
while m < n:
if n % m == 0:
p = False
m = m + 1
if p:
print ('Введённое число является простым.')
else:
print ('Введённое число не является простым.')
Сохраним модуль и запустим его на выполнение. Введём число 6. Оно делится на 2 и на 3, поэтому не является простым. Программа вывела сообщение об этом. Снова запустим модуль и введём число 13. Это число действительно является простым. Программа работает правильно, но запустим её ещё раз и введём число 16 769 023. Программа вернула результат с заметной временной паузой. Это произошло потому, что в написанной программе при увеличении числа увеличивается количество проверок.
Для решения этой задачи есть несколько вариантов сокращения перебора чисел. Прежде всего, единожды проверив делимость числа на 2, можно больше не проверять его делимость на чётные числа, так как все они содержат двойку в разложении на простые множители. Таким образом мы сократим количество предполагаемых делителей почти в два раза. Так как n равно произведению двух квадратных корней из n, то при его разложении на два множителя, если один из них будет больше квадратного корня из n, то второй будет меньше квадратного корня из n. Поэтому нам достаточно перебирать возможные множители до квадратного корня из n. Также, найдя хотя бы один делитель числа, мы докажем, что оно не является простым, и после этого проверку продолжать не требуется. Таким образом, нам достаточно проверить делимость n на два и на все нечётные числа на промежутке [3; sqrt (n)].
Изменим написанную программу. Вначале проверим, не делится ли n без остатка на 2 и присвоим результат этой проверки переменной p. Так как мы проверили делимость n на 2, присвоим переменной m новое начальное значение – 3. В дальнейшем нам понадобится функция извлечения квадратного корня из модуля math. Подключим этот модуль. Теперь изменим цикл проверки делимости числа n. Он будет работать пока m меньше либо равно квадратному корню из n. Так как квадратный корень из n – вещественная функция, в её значении может быть вычислительная ошибка, поэтому прибавим к её значению ещё единицу. Чтобы цикл завершил свою работу, как только будет доказано, что n не является простым, усложним условие цикла, соединив нынешнее условие конъюнкцией со значением переменной p. То есть цикл будет работать, пока значение m меньше или равно квадратному корню из n плюс один И в переменной p хранится значение «истина». В цикле значение переменной m будем увеличивать на 2, чтобы, пропуская чётное число, сразу переходить к следующему, нечётному.
print ('Программа, определяющая, является ли целое положительное число простым. Введите число.')
n = int (input ())
p = n % 2 != 0
m = 3
import math
while m < math.sqrt (n) + 1 and p:
if n % m == 0:
p = False
m = m + 2
if p:
print ('Введённое число является простым.')
else:
print ('Введённое число не является простым.')
Сохраним изменённый модуль и запустим его на выполнение. Чтобы подтвердить, что модуль работает правильно, сначала введём число 4. Оно делится на два, а потому не является простым. Снова запустим модуль и введём число 5. Это число действительно является простым. Теперь введём число 16 769 023. Программа мгновенно вывела сообщение о том, что это простое число. То есть сокращение перебора предполагаемых делителей подействовало. Не сложно рассчитать, что для последнего теста при изменении программы мы сократили количество проверок с 16.8 миллиона до 2 тысяч, поэтому скорость исполнения программы значительно увеличилась.
Мы узнали:
· Циклическим называется алгоритм, содержащий циклы.
· Цикл – это алгоритмическая конструкция, которая представляет собой последовательность действий, повторяющихся многократно.
· Цикл с заданным условием продолжения работы или с предусловием работает пока выполняется его условие.
· При увеличении количества повторений цикла, увеличивается время исполнения программы.

 Получите свидетельство
Получите свидетельство Вход
Вход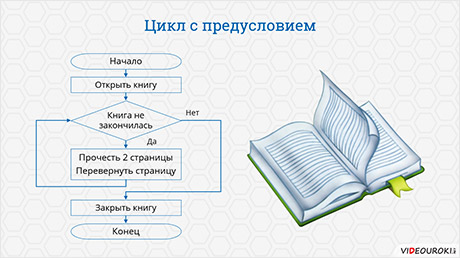



 0
0 15130
15130

