Во многих случаях алгоритм некоторых действий зависит от условий. В записях таких алгоритмов присутствуют конструкции ветвления. Однако в ветвлении рассматривается всего одно условие, которого может быть недостаточно. Сегодня мы изучим способы, которые позволяют обойти эти ограничения – сложные условия и каскадные ветвления.
Рассмотрим задачу. Прямоугольник на координатной плоскости со сторонами, параллельными координатным осям, задан координатами левой верхней и правой нижней своих вершин. Также даны координаты точки на плоскости. Все координаты – целые числа. Определить, принадлежит ли точка заданному прямоугольнику. Рассмотрим, как должна располагаться точка, чтобы принадлежать прямоугольнику. Относительно левой верхней вершины точка должна находиться не выше и не левее её. То есть координата x точки должна быть больше либо равна координате x вершины, а координата y точки должна быть меньше либо равна соответствующей координате вершины. Рассмотрим положение точки относительно правой нижней вершины. Точка должна находиться не ниже и не правее её. То есть координата x точки должна быть меньше или равна соответствующей координате вершины, а координата y точки должна быть больше либо равна соответствующей координате вершины. Таким образом, мы получили четыре неравенства, в случае выполнения которых точка будет принадлежать прямоугольнику.
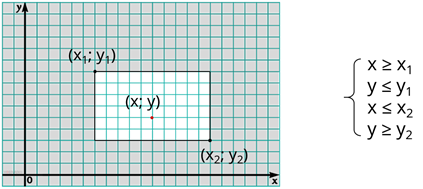
Так как это сложное условие, то прежде, чем приступить к написанию программы, составим блок-схему алгоритма решения задачи. Вначале программа будет принимать на вход координаты двух вершин прямоугольника и точки. Дальше будет следовать первое ветвление, условием которого будет первое неравенство. Если это условие не выполняется – точка не принадлежит прямоугольнику, и мы выведем сообщение об этом. Если же условие выполняется, то следует второе ветвление с определённым неравенством в качестве условия. Если условие этого ветвления не выполняется, то точка также не принадлежит прямоугольнику. Если же условие выполняется, то мы аналогичным способом проверяем выполнение двух оставшихся неравенств. Таким образом, если все условия выполняются, значит точка принадлежит прямоугольнику. Если не выполняется хотя бы одно из условий – точка не принадлежит прямоугольнику.
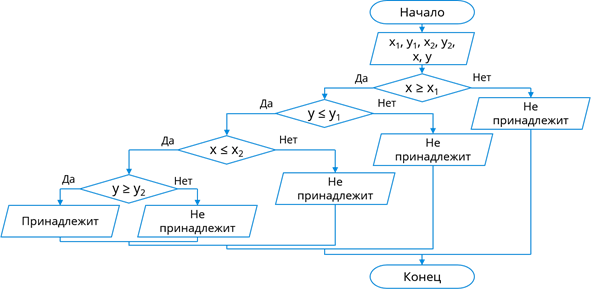
Как видим, мы получили блок-схему с использованием нескольких ветвлений, которые записаны в составе других ветвлений; они называются вложенными. Код программы, составленной по такой блок-схеме, будет достаточно сложен.
Но на самом деле эту задачу можно решить куда проще. Как мы помним, условиями ветвлений являются логические высказывания. Логические высказывания делятся на простые и сложные. До этого мы рассматривали простые логические высказывания. В них ни одна из частей сама по себе не является логическим высказыванием. Сложные же логические высказывания состоят из простых, соединённых с помощью логических операций.
Есть 3 основные логические операции, 2 из которых – бинарные, то есть соединяют 2 выражения логического типа. Первая логическая операция – конъюнкция или логическое умножение. В русском языке для её обозначения используют союз «И». В языке Python она обозначается словом and. Конъюнкция возвращает значение «истина» тогда и только тогда, когда истинны оба соединяемых высказывания.
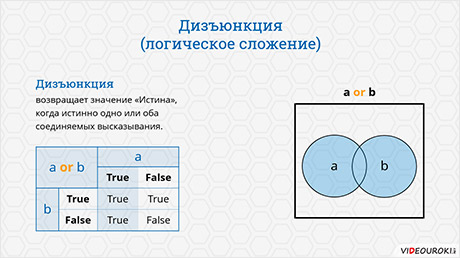
Вторая логическая операция – дизъюнкция или логическое сложение. В русском языке она обозначается союзом «или», а в языке Python – служебным словом or. Дизъюнкция возвращает значение «истина» тогда, когда истинно хотя бы одно или оба соединяемых высказывания.
И последняя из основных логических операций – инверсия или логическое отрицание. Эта операция является унарной, то есть применяется к одному логическому выражению. Инверсия изменяет значение выражения, к которому применяется, на противоположное. В русском языке она обозначается частицей «не», а в языке Python – служебным словом not.
Логические операции выполняются в самую последнюю очередь, даже после операций сравнения. Таким образом, логические операции имеют самый низкий приоритет выполнения.
Вернёмся к решению задачи о принадлежности точки прямоугольнику. Некоторые из вас уже наверняка догадались, что решение этой задачи можно сильно упростить, если записать сложное условие принадлежности точки прямоугольнику. Обратим внимание на то, что первое и третье неравенства можно объединить так же, как второе и четвёртое. Объединённые неравенства будут работать и в языке Python так же, как и одиночные, соединённые операцией конъюнкции. То есть сложную конструкцию, состоящую из четырёх ветвлений, можно заменить всего одним ветвлением, условием которого будут два неравенства. То есть точка принадлежит прямоугольнику, если её координата x больше либо равна координате x левой верхней вершины треугольника, а также меньше либо равна координате x правой нижней вершины прямоугольника И координата точки y меньше или равна координате y левой верхней вершины прямоугольника, а также больше либо равна координате y правой нижней вершины прямоугольника. Если это условие выполняется, тогда точка принадлежит прямоугольнику, в противном случае – точка не принадлежит прямоугольнику. Таким образом, для решения задачи нам достаточно всего одного ветвления.
Напишем программу для решения задачи. Вначале выведем на экран сообщение о том, что это программа, определяющая принадлежность точки прямоугольнику. С помощью второй инструкции print выведем на экран запрос на ввод координат верхней левой вершины прямоугольника. Дальше запишем инструкцию для считывания этих координат в переменные x1 и y1. Так как по условию задачи координаты – целые числа, то при считывании мы будем преобразовывать их значения в целочисленный тип int. Теперь дважды скопируем последние две инструкции и изменим их соответственно для считывания координат нижней правой вершины в переменные x2 и y2, а также для считывания координат точки в переменные x и y. Теперь запишем инструкцию ветвления с условием, состоящим из двух полученных ранее неравенств, соединённых служебным словом and. Если это условие выполняется, то выведем на экран сообщение о том, что точка принадлежит прямоугольнику. В противном случае, выведем сообщение о том, что точка не принадлежит прямоугольнику.
print ('Программа, определяющая принадлежность точки \nпрямоугольнику.')
print ('Введите координаты левой верхней вершины \nпрямоугольника.')
x1, y1 = int (input ()), int (input ())
print ('Введите координаты правой нижней вершины \nпрямоугольника.')
x2, y2 = int (input ()), int (input ())
print ('Введите координаты точки.')
x, y = int (input ()), int (input ())
if x2 >= x >= x1 and y2 <= y <= y1:
print ('Точка принадлежит прямоугольнику.')
else:
print ('Точка не принадлежит прямоугольнику.')
Сохраним написанный модуль и запустим его на выполнение. Зададим верхнюю левую вершину прямоугольника в точке (1; 7), а правую нижнюю – в точке (10; 2). Зададим точку (3; 3). Эта точка принадлежит заданному прямоугольнику. Программа вывела сообщение об этом. Снова запустим модуль. Зададим вершины прямоугольника в тех же точках, что и в прошлый раз, а также точку с координатами (7; 10). Заданная точка не принадлежит прямоугольнику. Программа вывела сообщение об этом, значит она работает правильно. Задача решена.
Рассмотрим ещё одну задачу. Написать программу для решения квадратных уравнений. Как мы знаем, квадратное уравнение имеет вид: ax2 + bx + c = 0. При этом a ≠ 0. Таким образом, квадратное уравнение можно задать значениями его коэффициентов: a, b и c.
Составим блок-схему алгоритма решения задачи. Вначале программа будет принимать на ввод коэффициенты уравнения: a, b и c. Далее мы должны вычислить значение дискриминанта уравнения. Для этого переменной D мы присвоим значение b2 – 4ac. Далее, как мы помним, нам нужно проверить значение дискриминанта. Если оно отрицательное, то уравнение не имеет решений. Если дискриминант равен нулю, то уравнение имеет единственное решение, которое вычисляется, как b – 2a. Если же дискриминант положительный, то уравнение имеет два решения, которые вычисляются по формуле:
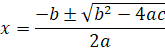
Чтобы это реализовать, сначала мы запишем ветвление с условием, что дискриминант отрицательный. Если это условие выполняется – уравнение не имеет решений, и мы выведем сообщение об этом. Если же условие не выполняется, то мы запишем второе ветвление с условием, что дискриминант равен нулю. Если это условие выполняется, то уравнение имеет одно решение. Мы вичислим его значение в переменной x, после чего выведем результат на экран. Если же и это условие не выполняется, значит дискриминант положительный и уравнение имеет два решения. Мы вычислим эти решения в переменных x1 и x2, после чего выведем их на экран. На этом работа программы будет завершена.
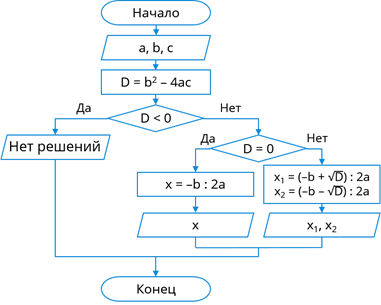
Как видим, наличие вложенного ветвления в одной из ветвей внешнего реализует разделение кода на три ветви. В языке Python разделение кода более чем на две ветви реализуется с помощью каскадного ветвления. Рассмотрим его запись. Как мы помним, обычное ветвление записывается так… Однако между блоками if и else можно добавить ещё один блок – elif с некоторым условием и инструкциями. Это ветвление работает таким образом, что сначала будет проверено условие в блоке if. Если это условие выполняется, то будут выполнены инструкции, записанные в этом блоке. Если же условие в блоке if не выполняется, то будет проверено условие в блоке elif. Если оно выполняется, то будут выполнены инструкции, записанные в этом блоке, если же и это условие не будет выполняться, то будут выполнены инструкции из блока else. Блоков elif может быть несколько, их условия будут проверяться сверху вниз, при этом будут выполнены инструкции, записанные в каком-то одном из блоков.
Используя каскадное ветвление, напишем программу для решения задачи. Вначале с помощью инструкции print выведем сообщение о том, что это программа для решения квадратных уравнений и запрос на ввод его коэффициентов. Дальше запишем инструкцию для считывания коэффициентов квадратного уравнения. В условии не сказано, что это целые числа, поэтому при считывании их значения мы будем преобразовывать в вещественный тип float. Далее вычислим значение дискриминанта в переменной D. Так как в дальнейшем нам понадобится функция извлечения квадратного корня, загрузим её в наш модуль из модуля math. Далее запишем инструкцию ветвления с условием, что дискриминант меньше нуля. Если это условие выполняется, то выведем на экран сообщение о том, что уравнение не имеет решений. Дальше запишем блок elif с условием, что D = 0. В случае выполнения этого условия мы вычислим решение уравнения в переменной x. Далее выведем на экран с соответствующим поясняющим сообщением значение переменной x. В блоке else мы вычислим два решения уравнения в переменных x1 и x2, после чего с соответствующим поясняющим сообщением выведем на экран их значения.
print ('Программа для решения квадратных уравнений.\nВведите коэффициенты уравнения.')
a, b, c = float (input ()), float (input ()), float (input ())
D = b ** 2 - 4 * a * c
from math import sqrt
if D < 0:
print ('Заданное уравнение не имеет решений.')
elif D == 0:
x = -b / (2 * a)
print ('x =', x)
else:
x1 = (-b + sqrt (D)) / (2 * a)
x2 = (-b - sqrt (D)) / (2 * a)
print ('x1 =', x1, 'x2 =', x2)
Сохраним модуль и запустим его на выполнение. Введём коэффициенты уравнения равными 1, 8 и 7. Таким образом, мы получим уравнение x2 + 8x + 7 = 0. Оно действительно имеет два решения: -1 и -7. Снова запустим модуль на выполнение и зададим коэффициенты уравнения равными 2, 4 и 2. Мы получим уравнение 2x2 + 4x + 2 = 0. Оно действительно имеет одно решение: –1. И снова запустим модуль на выполнение и зададим коэффициенты, равные 7, -1 и 3. Мы получим уравнение 7x2 – x + 3 = 0. Оно действительно не имеет решений. Программа работает правильно. Задача решена.
Мы узнали:
· Вложенным называется ветвление, которое находится в одной из ветвей другого ветвления.
· Сложные условия состоят из простых логических высказываний, соединённых с помощью логических операций.
· Основные логические операции: конъюнкцию, дизъюнкцию и инверсию.
· Каскадные ветвления используются для разделения кода более чем на две ветви.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 12181
12181

