Как мы свами выяснили на прошлых уроках, электромагнитная индукция проявляется во всех случаях изменения магнитного потока через поверхность, ограниченную контуром. Современник Фарадея американский физик Джозеф Генри примерно в тоже время, что и Фарадей, пытался превратить магнетизм в электричество. И несмотря на то, что удалось ему это сделать немного позже, чем Фарадею, Генри удалось открыть некоторые важные электромагнитные эффекты. В частности, Генри обнаружил, что ЭДС индукции может возникнуть в неподвижном контуре и в отсутствие изменения внешнего магнитного поля. Оказалось, что переменный электрический ток, проходящий в контуре, создаёт изменяющийся магнитный поток. Это явление было названо самоиндукцией.
Пронаблюдать за явлением самоиндукции можно на таком опыте. Соберём цепь, состоящую из источника тока, ключа, двух одинаковых лампочек, катушки с сердечником и резистора, сопротивление которого такое же, как и у обмотки катушки. Замкнём цепь. Как вы могли заметить, лампочка, соединённая последовательно с резистором, загорелась практически моментально. А вот вторая, соединённая с электромагнитом, с заметным опозданием (в реальном времени задержка составляет порядка одной секунды).
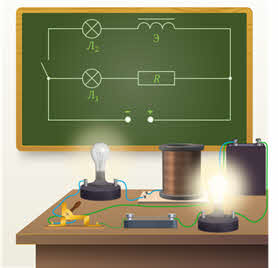
Объяснить этот опыт нам поможет правило Ленца. Итак, в момент замыкания цепи в катушке электромагнита возникает магнитное поле, которое постепенно увеличивается с ростом силы тока в витках катушки. Это приводит к тому, что увеличивается и магнитный поток, пронизывающий витки катушки. Мы уже знаем, что при изменении магнитного потока в витках катушки возникает индукционный ток, который препятствует увеличению силы тока в обмотке катушки. Когда же ток в катушке достигает постоянной величины, изменение магнитного потока прекращается и индукционный ток исчезает.
Самоиндукция является важным частным случаем явления электромагнитной индукции. Мы уже показали, что если электрический ток в замкнутом проводящем контуре меняется по каким-либо причинам, то пропорционально будет изменяться и магнитное поле этого тока (B ~ I). Но при изменении индукции магнитного поля, создаваемого током в контуре, пропорционально изменяется и магнитный поток (Ф ~ B). Поэтому, магнитный поток через поверхность, ограниченную контуром, будет пропорционален силе тока в контуре: (Ф ~ В ~ I).
В 1853 году Уильямом Томсоном предложил назвать коэффициент пропорциональности между магнитным потоком и силой тока коэффициентом самоиндукции (или просто индуктивностью контура):
Ф = LI.
Обозначается индуктивность большой латинской буквой L, а единицей её измерения в СИ служит генри, названная так, как вы догадались, в честь Джозефа Генри.
Индуктивность контура равна 1 Гн, если при силе тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб.
Индуктивность контура зависит от размеров и формы контура, а также от магнитных свойств среды, в которой находится этот контур.
Из формулы для магнитного потока следует, что изменить его можно тремя способами:
· изменяя силу тока в контуре;
· изменяя его индуктивность;
· или изменяя и то, и другое одновременно.
Если в контуре проходит постоянный ток, то вокруг контура существует постоянное магнитное поле. В этом случае собственный магнитный поток, пронизывающий контур, с течением времени остаётся постоянным, и ЭДС индукции в этом контуре не возбуждается.
Если же проходящий в контуре ток со временем изменяется, то происходит изменение и собственного магнитного потока. Согласно закону электромагнитной индукции, это приводит к возникновению электродвижущей силы в контуре, которую называют электродвижущей силой самоиндукции (или просто ЭДС самоиндукции) и обозначают ξsi.
Тогда можно сказать, что явление самоиндукции заключается в возникновении ЭДС индукции в самом проводнике, по которому протекает переменный электрический ток.
По закону электромагнитной индукции среднее значение ЭДС самоиндукции, возникающей в контуре с постоянной индуктивностью, прямо пропорциональна индуктивности контура и скорости изменения силы тока в контуре:
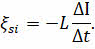
Из этой формулы следует, что индуктивность — это скалярная физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
Давайте теперь, для примера, определим собственный магнитный поток в конце процесса нарастания тока в катушке индуктивности, если за 10 мс сила тока равномерно возросла от 1,5 А до 2,5 А и при этом в катушке возникла ЭДС самоиндукции, равная –15 В.

В начале урока мы с вами показали проявление самоиндукции в момент замыкания цепи. Однако это явление можно пронаблюдать и при размыкании цепи. Давайте соберём электрическую цепь, состоящую из ключа и катушки с большим количеством витков, намотанных на железном сердечнике. Параллельно катушке подключим лампочку. Замкнув цепь, мы с вами наблюдаем очень тусклое свечение лампочки, поскольку отношение сил токов, проходящих через лампочку и катушку, обратно отношению их сопротивлений.
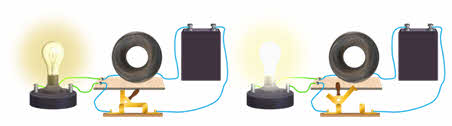
Однако при размыкании ключа происходит яркая кратковременная вспышка лампы.
В момент размыкании цепи сила тока в катушке постепенно убывает. Это приводит к возникновению ЭДС самоиндукции и, следовательно, тока самоиндукции. Этот ток, согласно правилу Ленца, совпадает по направлению с током катушки, не позволяя ему резко уменьшить силу тока. Это и обеспечивает вспышку лампочки.
Здесь мы с вами можем провести аналогию между самоиндукцией и явлением инерции в механике. Подобно тому, как явление инерции не даёт телу мгновенно изменить скорость под действием приложенной силы, явление самоиндукции не даёт току в цепи мгновенно приобрести определённое значение.
А теперь зададимся вопросом: откуда берётся энергия, обеспечивающая вспышку лампочки, ведь это не может быть энергия источника тока, так как он уже отключён. Ответ напрашивается сам собой: скорее всего запасённая в катушке в процессе самоиндукции энергия магнитного поля превращается во внутреннюю энергию спирали лампочки и энергию её излучения.
Проверим наше предположение с помощью небольшого опыта. Соберём электрическую цепь, состоящую из источника тока, двойного ключа, лампочки, катушки большой индуктивности, резистора и амперметра. Как видим, лампочка последовательно соединена с катушкой индуктивности. Ключ нам поможет замыкать цепь либо на источник тока, либо на активное сопротивление. Итак, для начала замкнём цепь на источник тока — амперметр фиксирует появление постоянного тока в цепи. А теперь при помощи ключа быстро замкнём катушку на резистор.
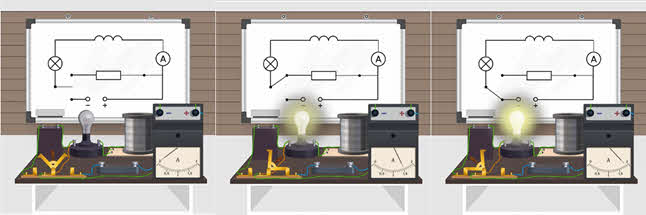
Амперметр сигнализирует нам о том, что сила тока в цепи со временем убывает. В течение этого времени всё ещё происходит перенос заряда в цепи катушки и резистора, то есть совершается работа. Эта работа и равна энергии магнитного поля катушки с током, так как именно энергия характеризует способность тел совершать работу.
Она равна половине произведения индуктивности контура и квадрата силы тока в нём:
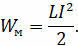
Используя выражение для магнитного потока, можно получить ещё две формулы для определения энергии магнитного поля тока:
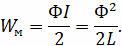

 Получите свидетельство
Получите свидетельство Вход
Вход




 6052
6052