На прошлом уроке мы с вами ввели в рассмотрение понятие магнитного потока (или потока вектора магнитной индукции). Напомним, что так называют скалярную физическую величину, равную произведению модуля индукции магнитного поля, площади поверхности, ограниченной контуром, и косинуса угла между направлениями нормали к этой поверхности и магнитной индукции:
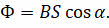
А ещё мы с вами познакомились с некоторыми опытами Майкла Фарадея, позволившие ему открыть одно из уникальных явлений современного мира — явление электромагнитной индукции. Давайте с вами вспомним, что это явление заключается в том, что при всяком изменении магнитного потока, пронизывающего замкнутый проводящий контур, в этом контуре возникает индукционный ток, существующий в течение всего времени изменения магнитного потока.
Но у нас с вами остался ещё один важный и нерешённый вопрос: какого же направление возникающего индукционного тока? Этим вопросом задавались многие учёные, среди которых был и петербургский академик Эмилий Христианович Ленц. В 1833 году после серии исследований явления электромагнитной индукции ему удалось сформулировать правило для определения направления индукционного тока — правило Ленца. Согласно этому правилу, возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, что созданный им магнитный поток через поверхность, ограниченную контуром, противодействует изменению магнитного потока, которым вызывается этот индукционный ток.
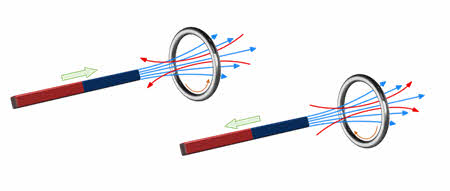
Правило Ленца можно проиллюстрировать на таком опыте. Возьмём два лёгких алюминиевых кольца, находящихся на острие подставки. Одно кольцо, как видно, сплошное. Другое же кольцо имеет небольшой разрез. Теперь возьмём постоянный магнит попробуем приблизить его к разрезанному кольцу. Как видим, разрезанное кольцо никак не реагирует на магнит. Это говорит нам о том, что индукционный ток в этом кольце не возникает.

А теперь попробуем приблизить магнит к сплошному кольцу. Как видим, оно отталкивается от магнита, подобно тому, как отталкиваются два одноимённых полюса магнита. И действительно, когда мы пытаемся внести магнит в кольцо, то в последнем возникает индукционный ток, который порождает в собственное магнитное поле. По правилу Ленца это поле имеет такое направление, что его линии индукции направлены противоположно линиям индукции внешнего поля магнита. Иными словами, кольцо и магнит оказываются обращёнными друг к другу одноименными полюсами.
Продолжим наши опыты. Но теперь, придерживая коромысло рукой, внесём магнит в сплошное кольцо. Отпустив коромысло, попробуем вытянуть магнит — кольцо следует за магнитом, подобно тому, как притягиваются два разноимённых полюса магнита. Объясним и этот случай. Когда мы пытаемся убрать магнит из кольца (то есть уменьшаем магнитный поток), то в кольце вновь возникает индукционный ток, но уже другого направления. Этот ток также порождает собственное магнитное поле. Однако линии индукции этого поля теперь направлены так же, как и линии индукции внешнего поля магнита. Иными словами, кольцо и магнит оказываются обращёнными друг к другу разноимёнными полюсами.
В более сжатой форме правило Ленца можно сформулировать следующим образом: индукционный ток всегда направлен так, что его действие противоположно действию причины, вызвавшей этот ток.
Индукционный ток, как и всякий ток, обладает энергией. Следовательно, получая индукционный ток, мы тем самым получаем электрическую энергию. Согласно закону сохранения и превращения энергии, последняя может быть получена только за счёт эквивалентного количества энергии какого-нибудь другого вида.
Когда мы приближаем, например, к катушке магнит, то возникающий в ней индукционный ток своим магнитным полем отталкивает магнит. Двигая магнит, мы преодолеваем эти силы отталкивания, то есть совершаем работу, в результате чего механическая энергия и превращается в энергию индукционного тока.
При выдвигании магнита из катушки совершается работа по преодолению силы притяжения катушки. Механическая энергия здесь также превращается в энергию индукционного тока. Таким образом, закон Ленца находится в полном соответствии с законом сохранения и превращения энергии.
Для того, чтобы определить направление индукционного тока по правилу Ленца, необходимо выполнить несколько нехитрых операций:
1) необходимо выяснить, как направлены линии магнитной индукции внешнего магнитного поля%
2) установить, увеличивается или уменьшается магнитный поток через поверхность, ограниченную проводящим контуром;
3) определить направление линий индукции магнитного поля индукционного тока. Для этого необходимо руководствоваться следующим: если изменение магнитного потока является величиной отрицательной, то направления индукций внешнего магнитного поля и магнитного поля индукционного тока совпадают, в противном случае эти направления противоположны.
4) узнав направление линий индукции магнитного поля индукционного тока, воспользоваться правилом буравчика для определения направления индукционного тока.
Открыв явление электромагнитной индукции, Фарадей буквально за полтора месяца установил все его существенные закономерности. Ему стала понятна сущность явления, которое сыграло такую важную, без преувеличения, роль для всего человечества: во всех проведённых опытах индукционный ток в проводящем контуре возникал только в результате изменения магнитного потока через поверхность, ограниченную этим контуром.
Как вы уже знаете, для существования тока в замкнутой электрической цепи необходимо, чтобы на свободные заряженные частицы действовали сторонние силы, то есть в цепи должен быть источник ЭДС. Вы, наверное, догадались, что в опытах Фарадея источником этих самых сторонних сил был изменяющийся магнитный поток, который и создавал в цепи электродвижущую силу. Эту ЭДС мы с вами будем называть электродвижущей силой индукции или, сокращённо, ЭДС индукцией.
Заметим, что для явления электромагнитной индукции именно ЭДС индукции является характерной величиной, а не индукционный ток, так как он зависит от сопротивления контура. Например, в двух одинаковых по размерам и форме проводниках при одинаковых условиях ЭДС индукции будет одинакова, а индукционный ток будет меньше в том проводнике, сопротивление которого больше.
Теперь, введя понятие ЭДС индукции мы можем дать более строгое определение явления электромагнитной индукции. Итак, явление возникновения ЭДС индукции в контуре, который либо покоится в изменяющемся во времени магнитном поле, либо движется в постоянном магнитном поле так, что магнитный поток через поверхность, ограниченную контуром, меняется, называют электромагнитной индукцией.
В 1873 году ещё один выдающийся английский физик Джеймс Клерк Максвелл, занялся анализом результатов опытов Фарадея. В частности, он заметил одно очень важное обстоятельство: чем быстрее меняется магнитный поток, пронизывающий контур, тем больший индукционный ток идёт по проводнику и, следовательно, тем большая ЭДС индукции в нём возникает:
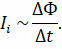
Однако из закона Ома для замкнутой цепи следует, что сила индукционного тока должна быть прямо пропорциональна ЭДС индукции и обратно пропорциональна сопротивлению проводника:
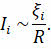
А так как сопротивление проводника не зависит от изменения магнитного потока, то выражение для силы индукционного тока будет справедливо только тогда, когда ЭДС индукции пропорциональна скорости изменения магнитного потока
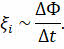
Чтобы обеспечить строгое равенство в записанном выражении, необходимо учесть направление индукционного тока. Как мы уже с вами выяснили, по правилу Ленца при увеличении магнитного потока ЭДС индукции отрицательная и, наоборот, при уменьшении магнитного потока ЭДС индукции положительная. Тогда можно записать, что ЭДС электромагнитной индукции в контуре равна скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой с противоположным знаком:
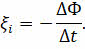
В этом и состоит математическая суть закона электромагнитной индукции, установленного Джеймсом Максвеллом и названного в честь Майкла Фарадея законом электромагнитной индукции Фарадея.
Для закрепления нового материала, давайте с вами решим такую задачу. И условие первой из них такое: в однородном магнитном поле, индукция которого равна 500 мТл, вращается стержень длиной 1 м с постоянной угловой скоростью 20 рад/с. Определите ЭДС индукцию, возникающую в стержне, если ось вращения проходит через конец стержня параллельно линиям магнитной индукции.

В заключении урока отметим, что наибольшего значения индукционные токи достигают в массивных проводниках. Такие токи принято называть токами Фуко́ по имени исследовавшего их французского физика Поль-Мишеля Фуко. Как правило, эти токи используются для нагревания проводников, например, в индукционных печах, современных индукционных плитах и так далее. Однако существует много устройств, в которых возникновение токов Фуко́ приводит к бесполезным, а порой и нежелательным потерям энергии на выделение тепла. Поэтому, например, в электродвигателях, генераторах, и трансформаторах железные сердечники выполняются не из сплошного металла, состоящие из отдельных пластин, изолированных друг от друга.

 Получите свидетельство
Получите свидетельство Вход
Вход




 12516
12516

