Прежде чем приступить к решению задач, стоит сказать, что графы, о которых пойдёт речь, к аристократам былых времён никакого отношения не имеют. У наших графов в корне есть греческое слово «графо», что значит «пишу». Этот же корень («граф») встречается, например, в словах «график, «биография», «орфография» и некоторых других.
Давайте выясним понятие графа на примере решения задачи.
В первенстве класса по настольному теннису шесть участников: Андрей, Саша, Вова, Оля, Дима и Лена. Каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Сашей, Олей и Леной; Саша, как уже говорилось, с Андреем и ещё с Олей; Вова – с Олей, Димой и Леной. Сколько игр уже проведено и сколько ещё осталось?
Итак, изобразим данные этой задачи в виде схемы. Участников первенства обозначим точками, расположив их по окружности: Андрей – А, Саша – ЭС, Вова – ВЭ, Оля – О, Дима – ДЭ, Лена – ЭЛЬ.
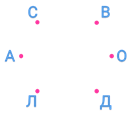
Если двое участников уже сыграли между собой, то будем соединять, обозначающие их точки отрезками. В условии задачи сказано, что Андрей сыграл с Сашей, Олей и Леной.
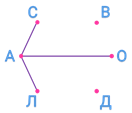
Мы уже видим, что Саша сыграл с Андреем, а ещё он сыграл с Олей.
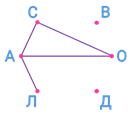
Вова сыграл с Олей, Димой и Леной.
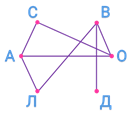
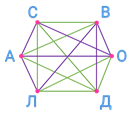
Получившаяся схема называется графом. Точки А, С, В, О, ДЭ, Л называются вершинами графа. Отрезки, которые соединяют вершины графа, называются рёбрами графа. Каждое ребро соединяет две вершины графа.
При этом обратите внимание, что точки, в которых пересекаются рёбра графа, не являются его вершинами.
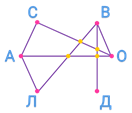
У графа 7 рёбер. Это означает, что к настоящему моменту было проведено 7 игр.
Чтобы найти количество игр, которые осталось провести, продолжим построение этого графа так, чтобы из каждой точки были проведены рёбра ко всем остальным точкам. Но для того, чтобы потом легче было подсчитать количество добавленных рёбер, рисовать их будем другим цветом.
Итак, известно, что Андрей сыграл с Сашей, Олей и Леной. А значит, он не играл с Вовой и Димой.
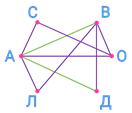
Также известно, что Саша сыграл с Андреем и с Олей, а значит, он не сыграл с Вовой, Димой и Леной.
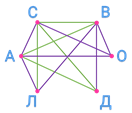
Вова сыграл с Олей, Димой и Леной. Получается, что он не сыграл с Андреем и Сашей. Но соответствующие отрезки уже проведены.
Оля сыграла с Андреем и Сашей, а также с Вовой. Это значит, что она ещё не сыграла с Димой и Леной.
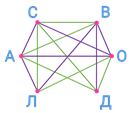
Дима сыграл только с Вовой. Ему предстоит сыграть с Олей, Сашей и Андреем, но эти отрезки мы уже провели. Осталось провести отрезок от Димы к Лене.
Лена сыграла с Андреем и Вовой. Ей предстоит сыграть с Димой, Олей и Сашей, но эти отрезки мы уже провели. Больше ничего добавлять не надо.
Мы добавили 8 рёбер. Это значит, что осталось провести ещё 8 игр. Получается, что ответ на вопрос задачи будет таким: проведено 7 игр, осталось провести 8 игр.
Отметим, что граф для одной и той же задачи можно нарисовать разными способами. И наоборот, для разных задач можно нарисовать одинаковые по виду графы.
Также отметим, что иногда рёбра удобнее изображать не отрезками, а «дугами».

Граф можно представить как набор пуговиц, некоторые из которых соединены нитями. Пуговицы – это вершины графа, нити – его рёбра.
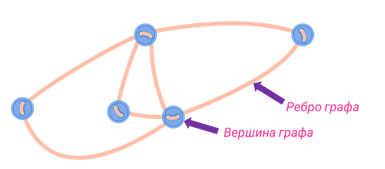
При этом, где именно расположены пуговицы, и как проходят нити не важно, ведь граф от этого не меняется. Важно то, какие пары пуговиц (то есть вершин графа) соединены нитями.
Но при решении задач, подобных приведённой, удобнее всё-таки располагать вершины по окружности. Тогда при проведении рёбер рисунок получается не таким запутанным.
Если из вершины графа выходит чётное количество рёбер, то её называют чётной. А если из вершины графа выходит нечётное количество рёбер, то её называют нечётной.
Посмотрите на такой граф.
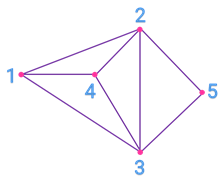
У него вершины 1 и 4 являются нечётными, так как из них выходят по 3 ребра.
А вот вершины 2, 3 и 5 являются чётными, так как из вершины под номером 2 выходят 4 ребра, из вершины под номером 3 тоже выходят 4 ребра, а из вершины под номером 5 выходят 2 ребра.
Решим следующую задачу. Встретились три подруги: Белова, Чернова и Краснова. На одной из них было чёрное платье, на другой – красное, на третьей – белое. Девочка в белом платье говорит Черновой: «Нам надо поменяться платьями, а то у всех троих цвет платьев не соответствует фамилиям». Кто в какое платье был одет?
На одном из наших занятий было предложено решить эту задачу с помощью таблицы. Давайте решим её с помощью рисунка.
Обозначим фамилии девочек буквами. Пусть напротив буквы Б будет белое платье, напротив буквы Ч – чёрное, напротив буквы К – красное.

Соединим пунктирной линией букву Б и белое платье. Это означает, что Белова не в белом платье. Также соединим пунктирными линиями букву Ч и чёрное платье, букву К и красное платье. Это означает, что Чернова не в чёрном платье, а Краснова не в красном платье.

В условии задачи говорится, что девочка в белом платье говорит Черновой: «Нам надо поменяться платьями, а то у всех троих цвет платьев не соответствует фамилиям». Получается, что Чернова одета не в белое платье. Поэтому соединим букву Ч с белым платьем пунктирной линией.
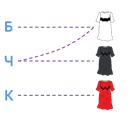
Теперь, внимательно посмотрев на рисунок, становится понятно, что ни Белова, ни Чернова не одеты в белое платье. Значит, в белое платье одета Краснова. Поэтому соединим букву К и белое платье сплошной линией.

Так как на Чернова была одета не в белое платье, а также на ней не могло быть чёрного платья, то, следовательно, она была в красном платье. Соединим сплошной линией букву Ч и красное платье.
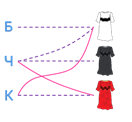
Мы выяснили, что Краснова была в белом платье, а Чернова была в красном. А значит, Белова была в чёрном платье. Соединим букву Б и чёрное платье сплошной линией.
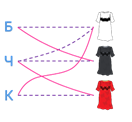
Ответ на вопрос задачи будет таким: Белова была одета в чёрное платье, Чернова – в красное платье, Краснова – в белое платье.
И решим ещё одну задачу. Из города А в город Б ведут 3 дороги, а из города Б в город Б – 4 дороги. Сколькими способами можно проехать из города А в город В, если по пути надо обязательно заехать в город Б?
Решение. Отметим точками города А, Б и В. В условии задачи сказано, что из города А в город Б ведут 3 дороги. Также сказано, что из города Б в город В ведут 4 дороги.

Возьмём одну дорогу, которая ведёт из города А в город Б. Её можно продолжить до города В четырьмя различными способами.
Если взять вторую дорогу, которая ведёт из города А в город Б, то и её можно продолжить до города В четырьмя различными способами.
То же самое можно сказать и про третью дорогу, ведущую из города А в город Б, то есть её также можно продолжить до города В четырьмя способами.
Получается, что по какой бы из трёх дорог из города А в город Б мы не поехали, продолжить дорогу в город В можно четырьмя способами.
Таким образом, из города А в город В через город Б можно проехать 3 умножить на 4, то есть 12 способами.
Ответ: 12 способов.

 Получите свидетельство
Получите свидетельство Вход
Вход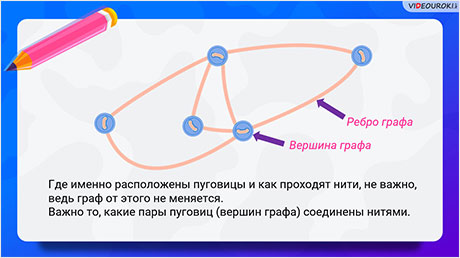




 8190
8190

