Здравствуйте, мальчики и девочки! Сегодня на занятии я хочу с вами поговорить об измерении площади и объёма, ведь в повседневной жизни мы часто сталкиваемся с такой необходимостью. Итак, если прочитать, что такое площадь, в словаре, то там написано, что площадь – это незастроенное большое и ровное место, например, в городе или селе, от которого обычно расходятся в разные стороны улицы. Например, вы все знаете Красную площадь в Москве или Дворцовую площадь в Санкт-Петербурге. Это может быть и небольшая сельская площадь. Ещё площадью часто называют помещение, предназначенное для какой-либо цели. Также вспомните про детскую площадку для игр или, к примеру, баскетбольную площадку. И конечно же, каждый из вас понимает смысл понятия площадь квартиры, площадь садового участка, площадь озера.
Ребята, если мы с вами нарисуем замкнутую линию (неважно, какой формы), то часть плоскости, заключённая внутри получившейся фигуры, – это и есть площадь.

Итак, площадь – это часть плоскости, ограниченная замкнутой кривой или ломаной линией.
На практике людям часто приходится сравнивать площади. Например, нам надо выяснить, какое из двух полей больше, чтобы узнать, для засева какого из них понадобится больше зерна. При решении этого вопроса нам неважно, какую форму имею поля. Нас интересует, какое из них занимает больше места, то есть имеет большую площадь. Предлагаю вам научиться сравнивать площади разных фигур.
Перед вами четыре фигуры (синяя, оранжевая, красная и зелёная). Конечно, можно сравнить площади этих фигур «на глаз».

Например, сравнить площади синей и оранжевой фигур совсем несложно, ведь сразу понятно, что площадь оранжевой фигуры меньше площади синей. Также очевидно, что и площадь красной фигуры меньше площади синей, и площадь зелёной фигуры тоже меньше площади синей.
Если же вы не уверены, что получится сравнить площади данных фигур «на глаз», то можно это сделать способом наложения.
Наложив оранжевую фигуру на синюю, мы увидим, что оранжевая меньше синей. Наложив красную фигуру на синюю, мы увидим, что красная намного меньше синей. Также можно убедиться наложением, что и зелёная фигура меньше синей.
Но не всегда площади фигур можно сравнить способом наложения.
Посмотрите, например, на вот такие две фигуры.

Сравнить их площади способом наложения довольно сложно. Лучше всего, конечно, сначала узнать площади этих фигур, а потом сравнить полученные результаты. Давайте поступим следующим образом: разобьём каждую из этих фигур на одинаковые квадраты и сосчитаем количество квадратов в каждой фигуре.

Очевидно, так как в первой фигуре помещается больше квадратов, чем во второй, то её площадь больше.
Ребята, думаю, вы убедились, что при помощи квадратов измерять и сравнивать площади фигур очень удобно. Если нам надо измерить площадь небольших геометрических фигур, например, таких, которые мы можем нарисовать в тетради, то в качестве мерного квадратика используют квадратный сантиметр, то есть квадрат, сторона которого равна 1 сантиметру.
Давайте посчитаем площадь данных фигур в квадратных сантиметрах. Итак, синяя фигура. В ней поместилось 25 квадратных сантиметров.

Оранжевая фигура. В ней поместилось 16 квадратных сантиметров.

Красный фигура. В ней пометилось 12 квадратных сантиметров.

И последняя, зелёная фигура. В ней поместилось 19 квадратных сантиметров.

Вот так при помощи квадратных сантиметров мы с вами измерили площади разных фигур.
Квадратный сантиметр – это единица измерения, которой удобно измерять площади небольших предметов. Например, таких, как книга, тетрадь, планшет. Площади предметов побольше можно измерить квадратными дециметрами. Например, площадь поверхности стола, площадь двери, площадь окна. Квадратными метрами удобно измерять площади помещений – комнат, коридоров, а также каких-то участков земли, например, детской площадки или садового участка. В квадратных километрах обычно измеряют площади городов, областей, государств. А вот квадратный миллиметр можно использовать, например, при измерении площади клеточки в школьной тетради.
Между единицами измерения площади существуют соотношения, которые всегда нужно помнить.

Находить площадь фигур, укладывая по всей их поверхности квадратики, довольно долго и не всегда удобно. Поэтому, если надо найти площадь прямоугольной поверхности (например, площадь окна или площадь пола в комнате), то можно воспользоваться формулой.

Так, площадь прямоугольника, у которого длина равна 8 сантиметрам, а ширина – 5 сантиметрам, равна произведению 8 и 5, то есть равна 40 квадратным сантиметрам.
А как быть, если надо найти площадь фигуры, которая не является ни прямоугольником, ни квадратом? Фигуры с искривлёнными извилистыми границами. Ребята, если эта фигура имеет не слишком большие размеры, то её площадь можно измерить с помощью палетки.
Палетка представляет собой прозрачную пластинку или плёнку с разлиновкой в клеточку. В зависимости от размера фигуры, площадь которой надо узнать, палетка может быть разделена на квадратные миллиметры, квадратные сантиметры, квадратные дециметры.

Давайте найдём площадь фигуры. Для этого возьмём палетку, которая разделена на квадратные сантиметры. Накладываем эту палетку на нашу фигуру так, чтобы, если это возможно, хотя бы одна сторона совместилась с линией разлиновки палетки. У нашей фигуры удалось совместить даже не одну, а две стороны. Обратите внимание, что даже уголки верхней и нижней сторон фигуры совпадают с уголками клеточек палетки.

Итак, сначала считаем, сколько всего целых квадратов, то есть квадратных сантиметров, укладывается в данной фигуре. Их 34.
Затем считаем все оставшиеся кусочки. Их 12. Каждые 2 таких кусочка принято засчитывать за 1 полный квадратик. Поэтому количество таких кусочков надо разделить на 2.
Теперь к 34 прибавляем частное 12 и 2. Получаем 40. Так как палетка разделена на квадратные сантиметры, то площадь фигуры примерно равна 40 квадратным сантиметрам. Примерно, потому что с помощью палетки вряд ли можно точно определить площадь фигуры.
Найдём площадь ещё одной фигуры. Снова воспользуемся палеткой, которая разделена на квадратные сантиметры.

Очевидно, что в данном случае совместить линии фигуры с разметкой палетки не получится.
Сначала считаем целые квадратики. Их 26.
Потом считаем кусочки. Их 21. Напомню, что 2 таких кусочка принято засчитывать за 1 полный квадратик, поэтому их количество надо разделить на 2. Но обратите внимание, что в данном случае количество кусочков – нечётное число. В таком случае на 2 надо делить ближайшее чётное число, которое больше данного на 1, то есть 22. Ведь всё равно с помощью палетки точно найти площадь фигуры невозможно.
Ребята, почему мы берём чётное число, которое больше данного, вы узнаете в пятом классе.
Таким образом, чтобы найти площадь данной фигуры, к 26 прибавим частное 22 и 2. Получим, что площадь примерно равна 37 квадратным сантиметрам.
Давайте повторим, как определить площадь фигуры с помощью палетки.
В первую очередь накладываем палетку на фигуру. Если границы этой фигуры представляют собой замкнутую ломаную, стараемся совместить хотя бы одну сторону и один угол с разметкой палетки. Считаем количество целых квадратов. Затем считаем количество кусочков. Делим количество кусочков на два. Складываем полученное число с количеством целых квадратов. Записываем ответ.
Кстати, с помощью палетки и плана местности можно найти площадь города, участка земли, озера и даже страны.
Ребята, мы с вами поговорили об измерении площади. Оставшуюся часть нашего занятия поговорим об измерении объёма литрами. Литр – это единица измерения объёма жидкости. Ею удобно пользоваться не только в математике, но и в жизни.
Например, в магазине многие продукты мы покупаем литрами. Причём не только в стеклянных банках, но и в пластиковых бутылках, картонных коробках, полиэтиленовых пакетах. На каждой ёмкости указано, сколько жидкости в ней помещено Вместо слова «литр» пишется маленькая буква «л». Причём точку после этого сокращения ставить не надо.
Ребята, в повседневной жизни часто возникает необходимость узнать, какое количество жидкости вмещается в какую-то ёмкость. Поэтому сейчас предлагаю вам выяснить, сколько жидкости, например, воды, помещается в банку.

Для этого в качестве меры объёма возьмём литровую кружку, наполненную водой.

Выльем воду из кружки в банку. Сейчас в банке 1 литр воды. Снова наполним кружку водой. Затем из кружки перельём воду в банку. Теперь в банке 2 литра воды. Опять наполним кружку водой и перельём эту воду в банку. Видим, что банка заполнилась водой. Всего мы налили 3 литра.

Вот таким образом, с помощью литровой кружки мы определили, что объём банки равен трём литрам. Таким же образом, можно определить, сколько жидкости вмещается в кастрюлю, в ведро, в бочку или какую-либо другую ёмкость.
Друзья, на этом время, отведённое на нашу встречу, заканчивается. Пора прощаться. До свидания. До новых встреч.

 Получите свидетельство
Получите свидетельство Вход
Вход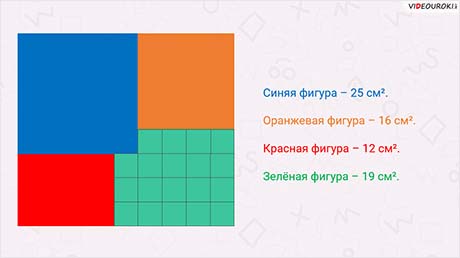




 882
882

