Вопросы:
· Тип данных float.
· Операции и функции обработки вещественных чисел.
· Функция генерации случайных вещественных чисел.
Итак, для хранения вещественных чисел в языке Python используются переменные типа float. Название этого типа является сокращением от англоязычного словосочетания floating point, что в переводе на русский язык означает «плавающая точка». Они получили такое название, потому что при хранении вещественных чисел в памяти компьютера их можно разделить на две части: мантиссу, то есть значимые цифры, и показатель сдвига относительно точки. В языке Python переменная вещественного типа float занимает 8 байт оперативной памяти. Это позволяет хранить до 15 значимых цифр в мантисе. Так как точность вещественных чисел при программировании ограничена, то в процессе проведения многочисленных вычислений с их использованием может накапливаться вычислительная ошибка, это стоит учитывать при написании программ, а также ни к чему использовать переменные вещественного типа для хранения целых чисел.
Рассмотрим, какие инструменты в языке Python используются для обработки вещественных чисел. Ранее мы уже рассмотрели основные арифметические операции: сложение, вычитание, умножение и деление, а также операцию возведения в степень. Мы узнали, что операция деления всегда возвращает результат вещественного типа, а результат остальных операций определяется их операндами. Если оба операнда или хотя бы один из них принадлежит к вещественному типу, то и результат операции будет принадлежать к вещественному типу. Также мы рассмотрели функцию вычисления модуля числа, тип результата которой всегда совпадает с типом аргумента.
В языке Python есть две встроенные функции для приведения вещественных значений к целочисленным. Это функции округления и выделения целой части числа, которые принимают в качестве аргумента вещественное число и преобразуют его в целое. Первая функция записывается словом round. Она округляет значение аргумента до целых по всем правилам математики, то есть при дробной части меньше пяти десятых значение числа округляется в меньшую сторону, а при дробной части, равной или большей пяти десятых, число округляется в большую строну. Вторая функция записывается служебным словом int. Она возвращает значение целой части аргумента, то есть просто отбрасывает дробную часть независимо от её значения.
Проверим работу изученных операций и функций путём решения задачи. Три резистора с известными сопротивлениями соединены параллельно в электрической цепи. Необходимо рассчитать их общее сопротивление и результат округлить до целых.
Обозначим сопротивления резисторов соответственно R1, R2 и R3. Мы знаем, что при параллельном соединении резисторов, будет справедливо следующее выражение:
где R0 – это общее сопротивление резисторов. Разделив единицу на левую и правую части выражения, мы получим формулу для вычисления общего сопротивления резисторов:
Напишем модуль для решения задачи. Сначала с помощью инструкции print выведем на экран сообщение о том, что это программа, рассчитывающая общее сопротивление трёх резисторов при их параллельном соединении, и запрос на ввод сопротивлений резисторов. Далее запишем инструкцию для считывания значений сопротивлений резисторов r1, r2 и r3. В условии не сказано, что их сопротивления – целые числа, поэтому при считывании мы будем преобразовывать введённые пользователем значения в вещественный тип float. Записав выражение для считывания первого сопротивления, скопируем его и для двух оставшихся. Далее запишем инструкцию присваивания переменной r0 значения общего сопротивления резисторов, рассчитанного по формуле, которую мы вывели. Теперь запишем инструкцию print для вывода сообщения о том, что общее сопротивление заданных резисторов при параллельном соединении равно значению переменной r0, округлённому до целых. Для округления значения r0 используем функцию round.
print ('Программа, рассчитывающая общее сопротивление 3 резисторов при их параллельном соединении. Введите сопротивления резисторов.')
r1, r2, r3 = float (input ()), float (input ()), float (input ())
r0 = 1 / (1 / r1 + 1 / r2 + 1 / r3)
print ('Общее сопротивление резисторов:', int (r0))
Сохраним написанный модуль и запустим его на выполнение. Введём значения сопротивлений резисторов: 10.5, 15 и 25. Программа вывела сообщение о том, что общее сопротивление заданных резисторов при параллельном соединении равно 5. Мы можем рассчитать общее сопротивление резисторов вручную или с помощью калькулятора и получим значение 4.95, что при округлении до целых даёт пять. Таким образом, мы подтвердили, что программа работает правильно.
Давайте попробуем в написанном нами модуле функцию округления round заменить функцией выделения целой части int. Сохраним получившийся модуль и запустим его на выполнение. Введём те же сопротивления резисторов, что и в первый раз: 10.5, 15 и 25. На этот раз программа вывела значение 4, то есть целую часть от действительного значения общего сопротивления.
Большинство математических функций в языке Python описаны в модуле math. На русский язык название этого модуля можно перевести как «математика». Рассмотрим некоторые функции, описанные в этом модуле. Это тригонометрические функции, возвращающие значения синуса и косинуса угла, заданного в радианах. Они записываются соответственно sin и cos. Для того, чтобы величину угла в градусах перевести в радианы, нужно его значение разделить на 180 градусов и умножить на π радиан. Есть функция, возвращающая квадратный корень из аргумента. Она записывается буквами sqrt. Есть ещё одна функция, которая возвращает экспоненту в степени аргумента. Она записывается служебным словом exp. Также есть функция, вычисляющая значение натурального логарифма из аргумента. Она записывается служебным словом log. Все описанные функции принимают на вход любой числовой аргумент, соответствующий их областям определения, и возвращают значение вещественного типа. Также в этом модуле хранится число π с точностью пятнадцать знаков после запятой. Чтобы его вызвать, достаточно обратиться к величине pi из этого модуля.
Для того, чтобы воспользоваться любой из этих функций, необходимо сначала подключить модуль math. Мы уже знаем, что это можно сделать, записав инструкцию import math. Далее можно будет использовать точечный вызов функций из этого модуля, при котором сначала записывается имя модуля, а через точку следует имя функции, но есть и другие способы воспользоваться функциями, описанными в модуле. Например, мы можем загрузить в рабочее пространство модуля, который мы описываем, все функции из модуля math, записав инструкцию from math import *. После этого, в описываемом модуле все функции из модуля math можно использовать как встроенные. Но такой способ вызова используется редко, так как при его применении, в описываемом модуле будут заняты все имена, совпадающие с именами функций из модуля math. Есть ещё один способ. Можно загрузить в рабочее пространство описываемого модуля только необходимые функции. Для этого записывается инструкция, начинающаяся со слов from math import, после которых, через запятую, перечисляются имена необходимых функций.
Если нужно сгенерировать случайное вещественное число, используется функция random из одноимённого модуля. Эта функция не имеет аргументов и возвращает случайное вещественное число на промежутке [0; 1). Однако, с помощью нехитрых преобразований, мы можем получить случайное вещественное число на любом промежутке. Если нам нужно получить случайное число на промежутке от a до b, не включая b, достаточно умножить значение функции на разность b и a и к полученному результату прибавить a.
Рассмотрим работу некоторых изученных функций путём решения задачи. Даны длины двух сторон треугольника и величина угла между ними (в градусах). Определить площадь заданного треугольника двумя способами: вычислением длины третьей стороны треугольника по теореме косинусов и применением формулы Герона; вычислением по известным длинам сторон и синусу угла между ними.
Теорема косинусов записывается следующим образом:
a2 = b2 + c2 – 2bc × cos α,
где a, b и c – это длины сторон треугольника, а α – это угол, противолежащий стороне a. Для того, чтобы вычислить косинус угла, величину этого угла нужно перевести в радианы, то есть нужно разделить её на 180 градусов и умножить на π радиан. Формула Герона выглядит так:
В ней p – это полупериметр треугольника. Формула площади треугольника по двум сторонам и синусу угла между ними выглядит так:
S = bc × sin α : 2.
Напишем модуль для решения задачи. С помощью инструкции print выведем на экран сообщение о том, что это программа вычисления площади треугольника. Далее запишем ещё одну инструкцию print. Она будет выводить на экран запрос на ввод длин двух сторон треугольника. Теперь запишем инструкцию для считывания длин сторон b и c. Так как в условии задачи не сказано, что это целые числа, при вводе будем преобразовывать их к вещественному типу float. Далее запишем инструкцию print, выводящую на экран запрос на ввод величины угла в градусах. Теперь запишем инструкцию для считывания в переменную ugol значения величины угла, которая также относится к вещественному типу Флоут. В нашей программе будет использоваться несколько функций из модуля math. Загрузим их в рабочее пространство модуля. Для этого запишем инструкцию from math import. Нам понадобятся функции синуса, косинуса и квадратного корня, а также величина pi. Теперь переведём величину угла в радианы. Для этого присвоим переменной ugol её собственное значение, делённое на 180 и умноженное на pi. По теореме косинусов найдём длину третьей стороны треугольника. Для этого переменной a присвоим величину, вычисленную по формуле. Теперь найдём полупериметр треугольника: переменной p присвоим значение суммы a, b и c, делённой на два. Далее вычислим площадь треугольника по формуле Герона. Для этого присвоим переменной s1 значение квадратного корня из произведения переменной p, разности p и a, разности p и b и разности p и c. Выведем значение вычисленной площади на экран с соответствующим поясняющим сообщением с помощью инструкции print. Форматируем вывод с помощью функции format. Выделим для вывода числа 5 знаковых позиций с двумя знаками после запятой. Теперь вычислим площадь треугольника вторым способом. Для этого переменной s2 присвоим произведение длин сторон b и c, а также синуса угла, делённое на два. С помощью инструкции print выведем значение площади на экран также, как и в первом случае.
print ('Программа, вычисляющая площадь треугольника.')
print ('Введите длины 2 сторон треугольника.')
b, c = float (input ()), float (input ())
print ('Введите величину угла между сторонами в градусах.')
ugol = float (input ())
from math import sin, cos, sqrt, pi
ugol = ugol / 180 * pi
a = sqrt (b ** 2 + c ** 2 - 2 * b * c * cos (ugol))
p = (a + b + c) / 2
s1 = sqrt (p * (p - a) * (p - b) * (p - c))
print ('S1 =', '{:5.2f}'.format (s1))
s2 = b * c * sin (ugol) / 2
print ('S2 =', '{:5.2f}'.format (s2))
Сохраним написанный модуль и запустим его на выполнение. Зададим длины сторон треугольника равными 9 и 10, а угол между ними – 90°. Так как это прямоугольный треугольник, его площадь можно вычислить как произведение известных сторон, делённое на 2. То есть 45. Программа вывела значения площади, рассчитанные двумя способами. Они также равны сорока пяти. Модуль работает правильно. Задача решена.
Мы узнали:
· Переменные для хранения вещественных чисел в языке Python занимают 8 байт оперативной памяти и позволяют хранить числа с точностью до пятнадцати значимых цифр.
· Для приведения вещественных чисел к целым используются встроенные функции округления и выделения целой части.
· Многие математические функции описаны в модуле math, например, квадратный корень, натуральный логарифм, синус и косинус угла.
· Для генерации случайных вещественных чисел используется функция random без параметров из одноимённого модуля.

 Получите свидетельство
Получите свидетельство Вход
Вход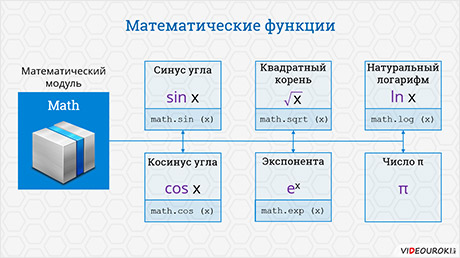



 0
0 4517
4517


