Выбор точки из фигуры на плоскости

Иногда случается, что на экране компьютерного монитора или смартфона перестаёт работать какой-то отдельный пиксель. В таком случае на экране появляется чёрная точка. Какова вероятность того, что неисправный пиксель попадёт в определённую область экрана?

Пикселей на экране может быть больше миллиона. Удобно считать, что мы имеем дело с точкой, выбранной случайным образом из прямоугольника.

Пример. Рассмотрим случайный эксперимент, в котором из прямоугольника со сторонами 7 и 3 выберем случайную точку. Какова вероятность того, что эта точка попала, например, в правый верхний квадрат со стороной 1?

В этой задаче речь идёт о геометрической вероятности. Разберёмся, что это за вероятность.

Иногда случайный эксперимент можно представить как выбор точки из некоторой фигуры на плоскости или из промежутка на прямой. В таком эксперименте каждое отдельное элементарное событие имеет нулевую вероятность, поэтому обычный способ подсчёта вероятностей не подходит. На помощь приходит геометрическая вероятность. В геометрических случайных экспериментах удобно считать, что событие и фигура – это одно и то же.

Элементарными событиями в рассматриваемом случайном эксперименте являются точки прямоугольника. Их очень много, и вероятность выбрать каждую конкретную точку равна 0.

Получается, что мы столкнулись с экспериментом, в котором элементарные события имеют нулевые вероятности, но не являются невозможными. Определить вероятность событий в этом эксперименте с помощью суммы вероятностей элементарных событий нельзя. Нужен другой способ.

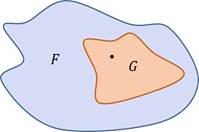
Рассмотрим более общий эксперимент. На плоскости дана фигура F, площадь которой не равна 0. Выберем из этой фигуры одну случайную точку. Какова вероятность того, что выбранная точка принадлежит фигуре G, которая содержится в фигуре F?

Ответ на этот вопрос зависит от того, как мы понимаем, что такое «случайно выбранная точка». Если мы считаем, что все точки должны «иметь равные шансы», то нужно принять некоторое правило.

Вероятность события «выбранная точка принадлежит фигуре G» прямо пропорциональна площади фигуры G и не зависит от расположения и формы фигуры G.

Вернёмся к эксперименту. Итак, точку мы выбрали из фигуры F, а значит, событие «точка принадлежит фигуре F» является достоверным, и его вероятность равна 1.

При таком подходе мы отождествляем (то есть не различаем) случайные события и геометрические фигуры. Поэтому событие и соответствующую ему фигуру будем называть одинаково.

Правило вычисления геометрической вероятности.

Вернёмся к первому примеру. Здесь фигура F – это прямоугольник со сторонами 3 и 7. Следовательно, площадь фигуры ЭФ равна 21.

Квадрат G, расположенный справа вверху в прямоугольнике F, имеет длину стороны, равную 1. А значит, площадь этого квадрата равна 1.

Решая такие задачи, мы предполагаем, что «шансы любой точки одинаковы». В большинстве случайных экспериментов это не так, но при определённых условиях можно считать, что наше предположение недалеко от истины.

Например, стрелок может попасть в любое место мишени. Но так как он стреляет не в случайное место, а целится, то вероятность попасть в центральный круг мишени несколько выше, чем вероятность попасть в круг где-то с краю.

Представим, что мишень очень мала, стрелок находится далеко от неё, а случайное рассеивание пуль во время стрельбы велико (оно может быть вызвано, например, ветром, ошибкой прицеливания, разогревом ружейного ствола и другими факторами). При этих условиях можно считать, что вероятность попасть в какую-то часть мишени главным образом зависит только от площади этой части и очень мало зависит о меткости стрелка.

Пример. Стрелок стреляет издалека по круглой мишени радиусом 5 см. Мишень разбита на три зоны. Радиус центральной круговой зоны равен 1 см. Средняя и внешняя зоны – кольцевые. Ширина каждой из них равна 2 см.

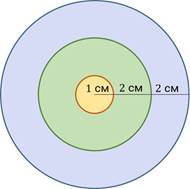
Известно, что стрелок попал в мишень. Давайте найдём вероятность того, что стрелок попал во внешнюю зону мишени.

В данном эксперименте фигурой F является мишень. Найдём её площадь как площадь круга с радиусом 5 сантиметров.

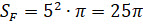 (см²)

Фигурой G является внешняя зона, то есть кольцо, у которого радиус внешней окружности равен 5 см, а внутренней – 3 см. Тогда площадь фигуры G найдём как разность площади круга с радиусом 5 см и площади круга с радиусом 3 см.

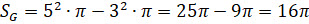 (см²)

Найдём вероятность того, что стрелок попал во внешнюю зону мишени, как частное площади фигуры G и площади фигуры F.

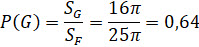
Найдём вероятность того, что стрелок попал в среднюю зону мишени.

Фигурой F является мишень. Её площадь нам известна.

Фигурой G в данном случае является средняя зона, то есть кольцо, у которого радиус внешней окружности равен 3 см, а внутренней – 1 см. Тогда площадь фигуры G найдём как разность площади круга с радиусом 3 см и площади круга с радиусом 1 см.

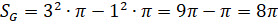 (см²)

Найдём вероятность того, что стрелок попал в среднюю зону мишени, как частное площади фигуры G и площади фигуры F.

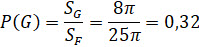
Найти вероятность того, что стрелок попал в центральную зону мишени.

Фигурой F является мишень. Её площадь нам известна.

Фигурой G является центральная зона, то есть круг, радиус которого равен 1 см.

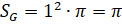 (см²)

Найдём вероятность того, что стрелок попал в центральную зону мишени, как частное площади фигуры G и площади фигуры F.

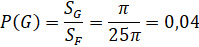
Иногда для поиска вероятностей не нужно знать площади фигур. Достаточно уметь находить отношения их площадей.

Пример. Дан треугольник АВС. Точки K, M и ЭN – середины сторон этого треугольника.

Из треугольника АВС случайным образом выбирается точка X. Найдём вероятность того, что точка X принадлежит треугольнику, вершинами которого являются середины сторон треугольника АВС.

Средние линии разбивают треугольник АВС на 4 равных треугольника, площадь каждого из которых обозначим Q.

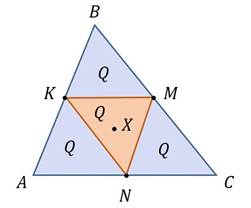
Получается, что площадь треугольника АВС в 4 раза больше, то есть равна 4Q.

Интересующее нас событие состоит в том, что точка X принадлежит треугольнику MNK. Вероятность этого события найдём как частное площади треугольника MNK и площади треугольника АВС.

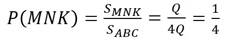
Выполним несколько заданий.

Задание первое. Внутри треугольника АВС случайным образом выбирается точка Х. Найдите вероятность того, что эта точка попала в треугольник АВМ, где АМ – медиана треугольника АВС.

Решение.

Задание второе. В квадрате АВСD случайным образом выбирается точка X. Найдите вероятность того, что эта точка принадлежит треугольнику АВM, где точка М – середина стороны ВС.

Решение.

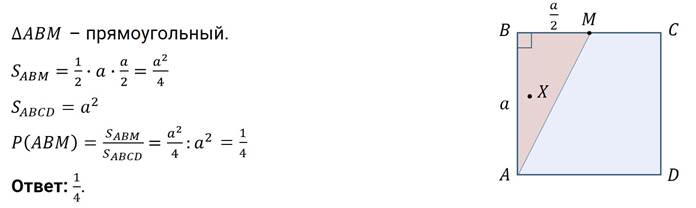До встречи на следующих занятиях!