Тест на повторение_ЕГЭ 11-15
Список вопросов теста
Вопрос 1
Автомобильный номер состоит из одиннадцати букв русского алфавита A, B, C, E, H, K, M, O, P, T, X и десятичных цифр от 0 до 9. Каждый номер состоит из двух букв, затем идет 3 цифры и еще одна буква. Например, АВ901С. В системе каждый такой номер кодируется посимвольно, при этом каждая буква и каждая цифра кодируются одинаковым минимально возможным количеством бит. Укажите, на сколько бит можно уменьшить размер памяти, выделенной для хранения одного номера, если кодировать с помощью минимально возможного количества бит каждую из трех групп – первые две буквы, три цифры и последняя буква.
Вопрос 2
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов.
1. заменить (v, w) 2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.
Дана программа для исполнителя Редактор:
ПОКА нашлось (5555) заменить (5555, 8) заменить (88, 5) КОНЕЦ ПОКА
Известно, что начальная строка состоит более чем из 400 цифр 5 и не содержит других цифр. При какой наименьшей длине исходной строки результат работы этой программы будет содержать наименьшее возможное число цифр 5?
Вопрос 3
На рисунке представлена схема дорог. Сколько существует различных путей из пункта А в пункт Б?
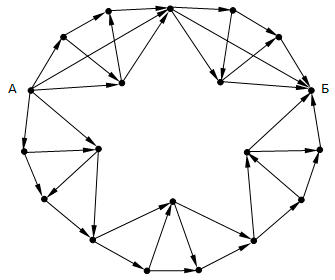
Вопрос 4
Значение арифметического выражения 103∙7103 – 5∙757 + 98 записали в системе счисления с основанием 7. Найдите сумму цифр получившегося числа и запишите её в ответе в десятичной системе счисления.
Вопрос 5
На числовой прямой даны три отрезка: P = [5, 110], Q = [15, 42] и R = [25, 70]. Какова наименьшая длина отрезка A, при котором формула
((x ∈ P) → (x ∈ Q)) ∨ (¬(x ∈ A) → ¬(x ∈ R))
тождественно истинна, то есть принимает значение 1 при любом значении переменной х?
Вопрос 6
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Сколько существует натуральных значений A на отрезке [1;1000], при которых формула
ДЕЛ(A, 7) ∧ (ДЕЛ(240, x) → (¬ДЕЛ(A, x) → ¬ДЕЛ(780, x)))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Получите комплекты видеоуроков + онлайн версии
 0
0 2610
2610 Нравится
0
Нравится
0

 Создать тест
Создать тест Вход
Вход








