Создать тест
ВходРешение квадратных неравенств
Список вопросов теста
Вопрос 1
На каком из рисунков изображено решение неравенства 25x2 > 49
Варианты ответов
Вопрос 2
Решите неравенство x2 - 64 > 0
Варианты ответов
-
\(\left(-\infty;+\infty\right)\)
- (-8;8)
-
\(\left(-\infty;-8\right)\cup\left(8;+\infty\right)\)
-
\(\left(8;+\infty\right)\)
Вопрос 3
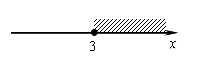
Решение какого из данных неравенств изображено на рисунке?
Варианты ответов
-
\(x^2+25\le0\)
-
\(x^2+25\ge0\)
-
\(x^2-25\le0\)
-
\(x^2-25\ge0\)
Вопрос 4
На каком рисунке изображено множество решений неравенства \(x^2-4x+3\ge0\)
Варианты ответов
-
\(\) -
-
\(\) -
Вопрос 5
Решите неравенство \(-x^2+5x\ge0\)
Варианты ответов
-
[0;5]
-
\(\left(-\infty;0\right)\cup\left(5;+\infty\right)\)
-
\(\left(-\infty;0\right)\cup\left[5;+\infty\right]\)
-
(0;5)
Вопрос 6
Решите неравенство \(9x^2+14x-3<4x^2\)
Варианты ответов
-
\(\left(-3;\frac{1}{5}\right)\)
-
\(\left[-3;\frac{1}{5}\right]\)
-
\(\left(-\infty;-3\right)\cup\left(\frac{1}{5};+\infty\right)\)
-
\(\left[-\infty;-3\right]\cup\left[\frac{1}{5};+\infty\right)\)
Вопрос 7
Укажите неравенство, которое не имеет решений:
Варианты ответов
-
\(x^2+6x+12>0\)
-
\(x^2+6x+12<0\)
-
\(x^2+6x-12<0\)
-
\(x^2+6x-12>0\)
Вопрос 8
Укажите неравенство, решением которого является любое число
Варианты ответов
-
\(x^2-92\ge0\)
-
\(x^2-92\le0\)
-
\(x^2+92\le0\)
-
\(x^2+92\ge0\)
Вопрос 9
На каком из рисунков изображено решение неравенства \((x-8)(x+6)\le0\)
Варианты ответов
Вопрос 10
При каких значениях x выражение \(\frac{1}{\sqrt[]{-x^2-8x-7}}\) имеет смысл?
Варианты ответов
-
\(\left(-\infty;-7\right]\cup\left[-1;+\infty\right)\)
-
\(\left[-7;-1\right]\)
-
\(\left(-\infty;-7\right)\cup\left(-1;+\infty\right)\)
-
\(\left(-7;-1\right)\)
Вопрос 11
Сколько целочисленных решений имеет неравенство \(x^2+5x-8<0\)
Получите комплекты видеоуроков + онлайн версии
0
557
Нравится
0
