Проверочная работа по темам (ЕГЭ13-18)_2вариант

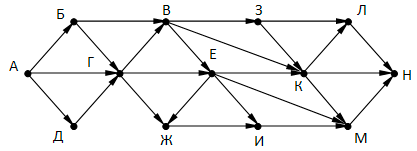
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М, Н. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. В ответе укажите последний в лексикографическом (алфавитном) порядке маршрут из города А в город Н, не проходящий через город Е и содержащий ровно восемь городов, включая города А и Н; города в маршруте указывайте заглавными буквами без разделителей.

Значение выражения 8⁸⁸⁸ + 16*16¹⁶¹⁶ – 2⁴⁴⁴ записали в системе счисления с основанием 8. Определите, сколько раз встречается максимальная цифра в этой записи?

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула

(ДЕЛ(x, 250) → ¬ДЕЛ(x, 10)) ∨ (3x + 2A ≥ 1000)

тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?

Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями:

F(0) = 3
F(n) = 1 + F(n / 2) если n > 0 и n чётное
F(n) = F(n // 2) в остальных случаях

Здесь // означает деление нацело. Определите количество значений n на отрезке [1, 1 000 000 000], для которых F(n) = 7.

В файле 17-292.txt содержится последовательность целых чисел. Элементы последовательности могут принимать целые значения от 0 до 10 000 включительно. Запишите в ответе количество пар элементов последовательности, в которых сумма остатков от деления обоих чисел на 6 совпадает с суммой остатков от деления этих чисел на 11. Затем запишите максимальную сумму чисел, составляющих такие пары. В данной задаче под парой подразумевается два идущих подряд элемента последовательности.

Квадрат разлинован на N×N клеток (1 < N < 30). Исполнитель Робот может перемещаться по клеткам, выполняя за одно перемещение одну из двух команд: вправо или вниз. По команде вправо Робот перемещается в соседнюю правую клетку, по команде вниз – в соседнюю нижнюю. При попытке выхода за границу квадрата Робот разрушается. Перед каждым запуском Робота в каждой клетке квадрата записано натуральное число, не превышающее 100. Перемещаясь по клеткам квадрата, Робот вычисляет сумму следующим образом. Начальное значение суммы - значение той клетки, из которой Робот начинает движение. При посещении клетки, Робот прибавляет к сумме удвоенное значение, записанное в клетке, если он попал в эту клетку из соседней сверху клетки, и прибавляет к сумме утроенное значение, записанное в клетке, если он попал в эту клетку из соседней слева клетки.
Определите максимальную и минимальную денежную сумму, которую может собрать Робот, пройдя из левой верхней клетки в правую нижнюю. В ответе укажите два числа – сначала минимальную сумму, затем максимальную.
Исходные данные для Робота записаны в файле 18-128.xls в виде прямоугольной таблицы, каждая ячейка которой соответствует клетке квадрата.