Перпендикулярность прямой и плоскости

Дан куб. Определи, какая из перечисленных в ответе прямых перпендикулярна названной плоскости?

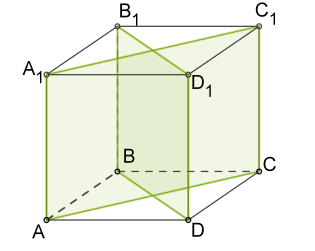
Плоскости (ABB1) перпендикулярна прямая

Дан куб. Определи, какая из перечисленных в ответе прямых перпендикулярна названной плоскости?

Плоскости (BDD1) перпендикулярна прямая

 В каком ответе проведённая прямая, которая не лежит в плоскости названной фигуры, перпендикулярна плоскости этой фигуры?

Прямая PQ параллельна плоскости α. 

От точек P и Q к плоскости проведены прямые PP1⊥α и QQ1⊥α. Известно, что PQ=PP1=8 см.

Определи вид четырёхугольника PP1Q1Q и найди его периметр.

(ответ: слово в именительном падеже, через пробел число. Например, параллелограмм 14)

Проведённая к плоскости перпендикулярная прямая пересекает плоскость в точке O.

На прямой отложен отрезок AD, точка O является серединной точкой этого отрезка.

Определи вид и периметр треугольника ABD, если AD= 18 см, а OB= 4 см (промежуточные вычисления и ответ округли до одной десятой)

(ответ: прилагательное в именительном падеже, через пробел число)

Две прямые образуют прямой угол с плоскостью α.

Длина отрезка KN= 33,5 cm, длина отрезка LM= 21,5 см. 

Рассчитай расстояние NM, если KL = 15 см.

Через вершину прямого угла C к плоскости прямоугольного треугольника ABC проведён перпендикуляр KC.

Точка D делит пополам гипотенузу AB.

Длина катетов треугольника AC = 72 мм и BC = 96 мм.

Расстояние KC = 11 мм. Рассчитай расстояние KD.

Отрезки KA=KC=KM не лежат в одной плоскости.

Известно, что ∡AKC=900, ∡MKC=900 и ∡MKA=600.

Которые из данных суждений действительны в этой ситуации?