ЕГЭ тест №19 (Вариант № 48632)

Список вопросов теста
Вопрос 1
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.
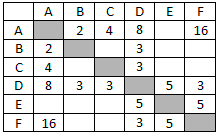
Определите длину кратчайшего пути между пунктами A и F, проходящего через пункт E и не проходящего через пункт B. Передвигаться можно только по указанным дорогам.
Вопрос 2
Логическая функция F задаётся выражением (x ∧ ¬y) ∨ (y ≡ z) ∨ w.

На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.
Вопрос 3
В файле 3-1.xls приведён фрагмент базы данных «Рейсы» о движении грузов на базе. База данных состоит из одной таблицы. Таблица «Рейсы» содержит записи о водителе, объеме перевезенного груза в килограммах и характере перевозки («привоз» на базу или «вывоз» с базы). На рисунке приведена схема данных.

Используя информацию из приведённой базы данных, определите сколько раз Уточкин и Сидоров вывезли с базы грузы объемом не менее 1500 кг и не более 2000 кг. В ответе запишите только число.
Вопрос 4
Для кодирования некоторой последовательности, состоящей из букв И, К, Л, М, Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К – кодовое слово 10. Какова наименьшая возможная суммарная длина всех пяти кодовых слов?
Вопрос 5
Автомат обрабатывает натуральное число N по следующему алгоритму:
1. Строится двоичная запись числа N без ведущих нулей.
2. Если в полученной записи единиц больше, чем нулей, то справа приписывается единица. Если нулей больше или нулей и единиц поровну, справа приписывается ноль.
3. Полученное число переводится в десятичную запись и выводится на экран.
Какое наименьшее число, превышающее 36, может получиться в результате работы автомата?
Вопрос 6
Запишите число, которое будет напечатано в результате выполнения следующей программы.
s = 33
n = 1
while s > 0:
s = s - 7
n = n * 3
print(n)
Вопрос 7
Музыкальный фрагмент был оцифрован и записан в виде файла без использования сжатия данных. Получившийся файл был передан в город А по каналу связи за 75 секунд. Затем тот же музыкальный фрагмент был оцифрован повторно с разрешением в 2 раза выше и частотой дискретизации в 3 раза выше, чем в первый раз. Сжатие данных не производилось. Полученный файл был передан в город Б за 90 секунд. Во сколько раз пропускная способность канала в город Б больше пропускной способности канала в город А?
Вопрос 8
Мила составляет 4-значные числа в 8-ичной системе. Сколько различных чисел, делящихся на 4 без остатка, может составить Мила?
Вопрос 9
Откройте файл электронной таблицы 9-0.xls, содержащей результаты ежечасного измерения температуры воздуха на протяжении трёх месяцев. Определите дату в мае, когда с 07:00 до 8:00 зарегистрировано наибольшее увеличение температуры. В ответе введите только одно число – номер дня. Если таких дней несколько, введите номер последнего такого дня.
Вопрос 10
С помощью текстового редактора определите, сколько раз, не считая сносок, встречается слово «разговор» (со строчной буквы, в любых падежах единственного и множественного числа) в тексте произведения А.С. Пушкина «Дубровский» (файл 10-106.docx). В ответе укажите только число.
Вопрос 11
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из 15 символов и содержащий только символы из 9 символьного набора: Д, В, А, Й, У, Ч, И, С, Ь. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения. На хранение дополнительных сведений отведен одинаковый для каждого пользователя объем памяти. Для хранения сведений о 40 пользователях потребовалось 480 байт. Какое максимальное количество бит может быть использовано для хранения дополнительных сведений об одном пользователе? В ответе запишите только целое число – количество бит.
Вопрос 12
Исполнитель Редактор получает на вход строку цифр и преобразовывает её. Редактор может выполнять две команды, в обеих командах v и w обозначают цепочки символов.
1. заменить (v, w) 2. нашлось (v)
Первая команда заменяет в строке первое слева вхождение цепочки v на цепочку w. Если цепочки v в строке нет, эта команда не изменяет строку. Вторая команда проверяет, встречается ли цепочка v в строке исполнителя Редактор.
Дана программа для исполнителя Редактор:
НАЧАЛО
ПОКА нашлось (4444) ИЛИ нашлось (7777)
ЕСЛИ нашлось (4444)
ТО заменить (4444, 77)
ИНАЧЕ заменить (7777, 44)
КОНЕЦ ЕСЛИ
КОНЕЦ ПОКА
КОНЕЦ
Какая строка получится в результате применения приведённой выше программы к строке, состоящей из 123 идущих подряд цифр 4? В ответе запишите полученную строку.
Вопрос 13
На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, не проходящих через город Г?
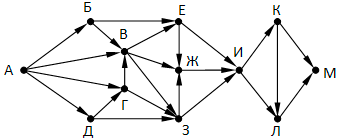
Вопрос 14
Значение выражения 6203 + 5∙6405 – 3∙6144 + 76 записали в системе счисления с основанием 6. Найдите сумму цифр получившегося числа и запишите её в ответе в десятичной системе счисления.
Вопрос 15
На числовой прямой даны два отрезка: P = [10, 80] и Q = [30, 50]. Найдите набольшую возможную длину отрезка A, при котором формула
(x ∈ A) → ((x ∈ P) ∧ ¬(x ∈ Q))
тождественно истинна, то есть принимает значение 1 при любых x.
Вопрос 16
Ниже записаны две рекурсивные функции (процедуры): F и G. Чему будет равно значение, вычисленное при выполнении вызова F(7)?
def F(n):
if n > 2:
return F(n-1) + G(n-2)
else:
return 1
def G(n):
if n > 2:
return G(n-1) + F(n-2)
else:
return 1
Вопрос 17
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 53. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 53 или больше камней.
В начальный момент в первой куче было 5 камней, во второй куче – S камней, 1 ≤ S ≤ 47. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Ответьте на следующие вопросы:
Вопрос 1. Известно, что Ваня выиграл своим первым ходом после неудачного первого хода Пети. Назовите минимальное значение S, при котором это возможно.
Вопрос 18
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 53. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 53 или больше камней.
В начальный момент в первой куче было 5 камней, во второй куче – S камней, 1 ≤ S ≤ 47. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Ответьте на следующие вопросы:
Вопрос 2. Найдите два таких значения S, при которых у Пети есть выигрышная стратегия, причём Петя не может выиграть первым ходом, но может выиграть своим вторым ходом независимо от того, как будет ходить Ваня. Найденные значения запишите в ответе в порядке возрастания (через пробел).
Вопрос 19
Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежат две кучи камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может добавить в одну из куч один камень или увеличить количество камней в куче в два раза. Чтобы делать ходы, у каждого игрока есть неограниченное количество камней. Игра завершается в тот момент, когда суммарное количество камней в кучах становится не менее 53. Победителем считается игрок, сделавший последний ход, т. е. первым получивший позицию, в которой в кучах будет 53 или больше камней.
В начальный момент в первой куче было 5 камней, во второй куче – S камней, 1 ≤ S ≤ 47. Будем говорить, что игрок имеет выигрышную стратегию, если он может выиграть при любых ходах противника.
Ответьте на следующие вопросы:
Вопрос 3. Укажите минимальное значение S, при котором у Вани есть выигрышная стратегия, позволяющая ему выиграть первым или вторым ходом при любой игре Пети, и при этом у Вани нет стратегии, которая позволит ему гарантированно выиграть первым ходом.
Вопрос 20
Ниже записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа a и b. Укажите наибольшее пятизначное число x, при вводе которого алгоритм печатает сначала 5, а потом 4.
x = int(input())
a = 0; b = 0
while x > 0:
y = x % 10
if y > 4: a = a + 1
if y < 6: b = b + 1
x = x // 10
print("%d\n%d" % (a, b))
Вопрос 21
У исполнителя Калькулятор три команды, которым присвоены номера:
1. прибавь 1 2. прибавь 3 3. прибавь 6
Программа для исполнителя – это последовательность команд. Сколько существует программ, которые число 21 преобразуют в число 30?
Получите комплекты видеоуроков + онлайн версии
 0
0 1088
1088 Нравится
0
Нравится
0

 Создать тест
Создать тест Вход
Вход








