Введение.
В настоящее время, согласно требованиям государственных стандартов и действующих программ обучения в медицинских учреждениях, основной задачей изучения дисциплины «Математика» является вооружение студентов математическими знаниями и умениями, необходимыми для изучения специальных дисциплин базового уровня, а в требованиях к профессиональной подготовленности специалиста заявлено умение решать профессиональные задачи с использованием математических методов.
Профессиональная направленность математической подготовки в медицинских образовательных учреждениях должна обеспечивать повышение уровня математической компетентности студентов-медиков, осознание ценности математики для будущей профессиональной деятельности, развитие профессионально значимых качеств и приемов умственной деятельности, освоение студентами математического аппарата, позволяющего моделировать,
анализировать и решать элементарные математические профессионально значимые задачи, воспитание у студентов потребности в совершенствовании знаний в области математики и ее приложений.
На первый взгляд медицина и математика могут показаться несовместимыми областями человеческой деятельности. Математика по общему признанию, является «царицей» всех наук, решая проблемы химии, физики, астрономии, экономики, социологии и многих других наук. Медицина же, долгое время развиваясь «параллельно» с математикой, оставалась практически неформализованной наукой тем самым подтверждая, что «медицина - это искусство».
Зачетное занятие
по теме: « Прикладные математические задания для зачёта »
Для решения задач по специальным предметам необходим следующий справочный материал:
1. Математика и этапы жизнедеятельности
а) Расчет прибавки роста детей
Прибавка роста детей после 1 года жизни расчитывается по формуле:
Р = 75+5n, где n-количество лет
б) Расчет прибавки массы детей
Наблюдение педиатров показывают, что ребенок до года,
в среднем набирает 7 кг. 150г. Это видно из таблицы
| 1 месяц | 600г. |
| 2 месяц | 800г. |
| 3 месяц | 800г. |
| 4 месяц | 750г. |
| 5 месяц | 700г. |
| 6 месяц | 650г. |
| 7 месяц | 600г. |
| 8 месяц | 550г. |
| 9 месяц | 500г. |
| 10 месяц | 450г. |
| 11 месяц | 400г. |
| 12 месяц | 350г. |
в) Расчет питания (объемный способ)
Суточный объем питания ребенка до
 до 2 месяцев 1/5
до 2 месяцев 1/5
2-4 1/6 от массы тела ребенка
4-6 1/7
6 1/8
Площади фигур.
Квадрат: S=a2= d2 , где а – сторона, d - диагональ
2
Прямоугольник: S= а · в, где а и в – сторона
Ромб: S= d1d2 = а2 · sin , где d1 и d2 – диагонали, а – сторона, – один из углов
2
Параллелограмм: S= а·h=a h sin , где а и h – стороны, h – высота,
- один из углов
Трапеция: S= a+b · h= c · h , где а и b – основания, h – высота, с – средняя
2
линия
Треугольник: S= 1 а h =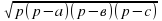 р(р-а) (р-в) (р-с), где а – основание, h – высота,
р(р-а) (р-в) (р-с), где а – основание, h – высота,
2 р – полупериметр
Круг: S=П d2 0,875d2, где d -диаметр
4 объемы фигур
Призма:V = S ·1, где S – перпендикулярное сечение, 1 – длина бокового ребра.
Куб: V = а2, где а – ребро куба
Пирамида: V =1 S · h, где S – площадь основания, h - высота
3
Цилиндр: V = Пr2 h, где r – радиус, h - высота
Конус: V =1 S · h, где S – площадь основания, h - высота
3
Шар: V =4 П · ч2 , где ч – радиус шара
3
в) Анатомия в педиатрии.
Кровь у новорожденного ребенка составляет 15% от массы тела,
у детей до года – 11% массы тела.
г) Кровеносная система.
Кровь у взрослого человека составляет 6-8% от массы тела.
Через почки в течение суток протекает 1500 л. крови, а вся кровь проходит
за 5 минут (5-6 литров).
д) Газообмен в легких.
При относительном покое взрослый человек совершает примерно
16 дыхательных движений в минуту. Жизненная емкость легких (ЖЕЛ):
 ЖЕЛ=ДО+РО6+РОвыд,
ЖЕЛ=ДО+РО6+РОвыд,
Где ДО – двхательный объем (0,5л.)
Ров – резервный объем вдоха (1,5л.) 3-4л.
РОвыд.- резервный объем выдоха (1,5л.)
Во вдыхаемом воздухе содержится:
- 20,97% кислорода
- около 70% азота
- небольшое количество водяных паров и инертных газов.
Процентный состав выдыхаемого воздуха иной:
- кислорода в нем остается около 16%
- количество углекислого газа возрастает до 4%
Математика и основы сестринского дела.
а) Процентом (от латинского рчо сеnto – c сотни) называется сотая часть. Запись 1% означает 0,01; 27%=0,27; 100%=1; 150%=1,5 и т.д.
Чтобы найти процентное выражение данного числа. Нужноумножить это число на 100 (или, что одно и то же, перенести в нем запятую на 2 знака вправо).
Чтобы найти число по его процентному выражению, нужно разделить процентное выражение на 100 (или, что одно и то же, перенести запятую на два значка влево).
б) Расчет в процентной концентрации растворов
(в различных объемах жидкости)
Данное число делится на 100, и полученный результат умножается на число процентов.
- Найти число по данной величине указанного его процента.
Данная величина делится на число процентов, и результат умножается на 100.
в) Найти выражение одного числа в процентах другого.
Умножаем первое число на 100; результат делим на второе число.
По определению концентрации чистого вещества в растворе – это количество граммов в 100 мл. Следовательно, для расчета количества вещества в 1 мл раствора необходимо имеющуюся массу чистого вещества в растворе разделить на 100.
Математика в анатомии.
а) Сердечно-сосудистая система
Масса сердца взрослого человека составляет 1/220 часть от массы тела (0,425-0,570 кг.). Масса сердца новорожденного в среднем 0,66-0,80% от массы тела (около 20г.) Параметры сердца взрослого человека: h-12-15см, поперечный разрез d1-8-10см., передний-задний разрез d2-5-8см. Для вычисления объема сердца используем формулу объема конуса:
V=1 sh= 1 ПR2h =1 П 2 h
3 3 12
б) Костно-мышечная система.
Для решения задач по данной тема необходимо знание площадей и объемов фигур.
Вариант № 1
Задача: При рождении ребенка его вес был 5 кг 600 г.
Каким будет его вес к 10 месяцам?
Задача: Рассчитать необходимое количество единиц инсулина (ЕД) при условии, что 1 ЕД расщепляет 5 г сахара сухого вещества, если
1) введено 10% глюкозы 800 мл;
2) введено 25% глюкозы 600 мл;
3) введено 20% глюкозы 350 мл;
4) введено 5% глюкозы 2 л.
Задача: Рассчитать разовую дозу прозерина
при введении пациенту:
а) I мл 0,05% раствора
б) 2 мл 0,05% раствора
Задача: Сколько кислорода вдохнул человек, если известно, что при нормальном дыхании во вдыхаемом воздухе содержится 21% кислорода, а жизненная емкость легких 4 000 см3?
Вариант №2
Задача : Ребенок родился с весом 3 кг 200 г.
Каким будет его объем питания в 1 месяц? В 4 месяца?
Задача: Больному назначен пенициллин 500 тыс. ЕД 4 раза в день в течение 7 дней. Больной попросил медсестру посчитать количество флаконов пенициллина, которое необходимо для лечения. Какой ответ больному дала медсестра, если 1 флакон содержит
а) 1 млн. ЕД
б) 500 тыс. ЕД
Задача: Рассчитать дозу сухого вещества кофеина бензоата натрия на один прием при назначении на прием столовой ложки 0,5% раствора (столовая ложка = 25 мл).
Задача: Масса головного мозга взрослого человека 1370 г. Сколько это процентов от всей массы тела, если вес человека 78 кг?
Вариант №3
Задача: За первые 3 месяца жизни ребенок набрал 1,3 кг. Сколько ребенок в 4 месяца, если он родился с весом 2,6 кг и за последний месяц жизни прибавил в весе среднестатистическое значение?
Задача: Рассчитать потерю жидкости в организме человека при полостной операции и температуре воздуха 38°С (потеря жидкости при полостной операции составляет 1 л, а на каждые 5°С свыше 25°С окру-
жающей среды теряется дополнительно 500 мл жидкости).
Задача: Сколько граммов фурацилина находится в:
а) 200 мл 0,02% раствора.
б) 500 мл 0.02% раствора?
Задача: На сколько изменилась масса крови ребенка 1 года жизни, если известно, что он родился с весом 3 кг 700 г.
Вариант №4
Задача: Рассчитать объем питания 4 месячного ребенка, если он родился с массой 4 кг 200 г и прибавлял в весе согласно табличным данным.
Задача: Введено 300 мл 20% глюкозы. Сколько единиц инсулина
(1 ЕД расщепляет 4 г сахара) нужно ввести пациенту для исключения
нарушения метаболических процессов в организме?
Задача: Чистого вещества в растворе 0,025%.
Сколько литров раствора можно получить из 30 граммов чистого вещества?
Задача: Рассчитать на сколько изменилась масса крови взрослого человека, если первоначальный нес его был 68 кг, а за 3 месяца он набрал 8 кг. за последние 2 месяца сбросил 4 кг?
Вариант №5
Задача: До 5 месяцев ребенок, родившийся с весом 4,2 кг, прибавлял в весе среднестатистическое значение веса, а за 5-й, 6-й, 7-й месяцы жизни ни набирал всего по 500 г.
Какой вес имел ребенок в 6 месяцев, а в 7 месяцев?
Задача: В больнице 190 койкомест. Из них заполнено больными 152 места. На сколько процентов заполнена больница?
Задача: Вычислите массу сердца новорожденного весом 4,5 кг. если известно, что масса сердца ребенка составляет 0,66% от массы тела.
Задача: Емкость мочевого пузыря 3-х месячного ребенка составляет 100 мл. Он заполнен на 25 %.
Сколько это мл мочи находится в мочевом пузыре?
Вариант №6
Задача: Рассчитать, на сколько больше пищи требуется 6- месячному ребенку, чем 2- месячному, если известно, что в 6 месяцев ребенок весит 5 800 г, а в 2 месяца - 4000 г.
Задача: Сколько единиц инсулина нужно ввести, если больному прокапали 200 мл 20% глюкозы (1 ЕД инсулина расщепляет примерно
4 г. сухого вещества сахара (глюкозы)?
Задача: Больному назначены таблетки бромгексин-4 три раза в сутки. Вместо вышеуказанного больной принимал бромгексин-8, но по соответствующей дозе. Сколько таблеток принял больной за сутки?
Задача: Объем крови у взрослого человека составляет 5 литров. При глубоком порезе он потеряет 8% от общего объема. Найти, какова потеря крови?
Ответы на вопросы к дифференциальному зачету
Вариант №1
1.Решение:
Р1г.=3600+600+800+800+750+700+650+600+550+500+450=10000 (г) = 10 кг000 г
Ответ: Вес ребенка 10 месяцев = 10 кг.
2.Решение:
1) 800:100*10:5=16 (ЕД)
2) 600:100*25:5=30 (ЕД)
3) 350:100*20:5=14 (ЕД)
4) 2000:100*5:5=20 (ЕД)
Ответ: 1) 16 (ЕД), 2) 30 (ЕД), 3) 14 (ЕД), 4) 20 (ЕД)
3.Решение:
а) 1:100*0,05=0,0005 (г)
б) 2:100*0,05=0,001 (г)
Ответ: а) 0,0005 г, б) 0,001 г
4.Решение:
а) 1500:100*21=315 см3 (т.к. резервный объем вдоха равен 1500 см3)
Ответ: 315 см3 кислорода вдохнул человек
Вариант №2
1.Решение:
1) Р1м = 3200+600 = 3800 г
2) V1м = 3800* 1/5 = 760 г
3) Р4м = 3800+800+800+750 = 6150
4) Р4м = 6150:1/6 = 1025
Ответ: объем питания месячного ребенка составляет 760 г, объем питания 4-месячного ребенка составляет 1025 г.
2.Решение:
а) 500 000*4*7 = 14 000 000 = 14 флаконов
б) 14 000 000:500 = 28 флаконов
3.Решение:
25:100*0,5 = 0,125 г
Ответ: 0,125 г
4.Решение:
78 000 – 100%
1370 – х
х = 1370*100:78 000 = 1,76%
Ответ: масса головного мозга взрослого человека 1,76% от массы тела
Вариант №3
1.Решение:
Р 4 мес. = 2,6+1,3+0,75 = 4,65 (кг)
Ответ: Вес ребенка 4 месяцев – 4 кг 650 г
2.Решение:
а) (38-25):5*500+1000 = 2300 мл = 2,3 л
Ответ: количество жидкости, которое теряет человек, равно 2
3.Решение:
а) 200:100*0,02 = 0,04 (г)
б) 500:100*0,02 = 0,1 (г)
Ответ: а) 0,04 г; б) 0,1 г
4.Решение:
1) 3,7:100*15 = 0,555 (кг)
2) (3,7+7,15):100*11 = 11,935 (кг)
3) 1,1935-0,555 = 0,6385 (кг)
Ответ: масса крови ребенка уменьшилась на 0,6385 кг
Вариант 4
1.Решение:
1) Р4м = 4200+600+800+800+750 = 7150 г
2) V4м = 7150*1/6 = 1197,67
Ответ: объем питания 4 месячного ребенка составляет 1197,67 г
2.Решение:
1) 300:100*20 = 60 (г)
2) 60:4 = 15 (ЕД)
Ответ: 15 ЕД нужно ввести пациенту для исключения нарушения метаболических процессов в организме
3.Решение:
1) 30:0,025*100 = 120 000 мл = 120 л
Ответ: 120 л
4.Решение:
(68+8-4):100*7 = 5,04 (кг) масса крови
68:100*7 = 4,76 (кг) исходная масса крови
5,04-4,76 = 0,28 кг = 280 г
Ответ: На 280 г изменилась масса крови взрослого человека
Вариант 5
1.Решение:
Р6 мес. = 4200+600+800+800+750+2*500 = 8150 (г) = 8,15 (кг)
Р7 мес.= 8,15+0,500 = 8,65(кг)
Ответ: Вес ребенка 6-ти месяцев – 8 кг 150 г, вес ребенка 7-ми месяцев = 8 кг 650 г
2.Решение:
152*100:190 = 80%
Ответ: 80%
3.Решение:
4,5 *0,66:100 = 0,0297 (кг) = 30 (г)
Ответ: Масса сердца новорожденного весом 4,5 кг составляет 30 г
4.Решение:
100:100*25 = 25 мл
Ответ: Мочевой пузырь заполнен на 25 мл
Вариант №6
1.Решение:
1) V6м = 5800*1/7 = 828,57 г
2) V2м = 4000*1/5 = 800 г
3 ∆ V = 828,57-800 = 28,57 г
∆ V = 828,57-800 = 28,57 г
Ответ: 828,57 г, 800 г, 28,57 г
2.Решение:
1) 200:100*20 = 40 (г)
2) 40:4 = 10 (ЕД)
Ответ: 10 ЕД нужно ввести пациенту для исключения нарушения метаболических процессов в организме
3.Решение:
1) 8/4 = 2, то есть вместо таблетки бромгексин-4, больной принимал ½ таблетки бромгексин-8
2) 3*1/2 = 1,5 (таблетки) принял больной за сутки
Ответ: 1,5 таблетки принял больной за сутки
4.Решение:
5:100*8 = 0,4 кг
Ответ: 0,4 кг потеря крови при глубоком порезе

 Получите свидетельство
Получите свидетельство Вход
Вход



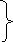 до 2 месяцев 1/5
до 2 месяцев 1/5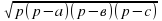 р(р-а) (р-в) (р-с), где а – основание, h – высота,
р(р-а) (р-в) (р-с), где а – основание, h – высота,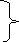 ЖЕЛ=ДО+РО6+РОвыд,
ЖЕЛ=ДО+РО6+РОвыд, ∆ V = 828,57-800 = 28,57 г
∆ V = 828,57-800 = 28,57 г








 Занятие по математике по теме: «Прикладные математические задания для зачёта» (34.14 КB)
Занятие по математике по теме: «Прикладные математические задания для зачёта» (34.14 КB)
 0
0 5488
5488 755
755 Нравится
0
Нравится
0


