"Задачи, приводящие к нормальному распределению. Функция плотности и свойства нормального распределения"

Федеральное Государственное Казенное Общеобразовательное Учреждение

«Кадетский корпус Следственного комитета Российской Федерации имени Александра Невского»

Задачи, приводящие к нормальному распределению. Функция плотности и свойства нормального распределения

Статистика и вероятность 11 класс

Учитель математики Щедрина Р.Н.

Познакомься с нормальным распределением случайной величины

Рассмотрим пример с доской Гальтона. Доска размещена вертикально. Из верхнего резервуара стальные шарики катятся (на отдельных участках падают) вниз и накапливаются в нижних гнездах. Каждый шарик, встретив на своем пути очередное препятствие, отклоняется или влево или вправо, а затем падает вниз. Шарик, конечно, может попасть в любое из гнезд. Между тем правильное расположение шариков (симметричное, при котором в центральных гнездах их много, а в крайних мало), повторяющееся от эксперимента к эксперименту, убедительно свидетельствует о существовании объективного закона их распределения.

Данный закон распределения случайной величины называется законом нормального распределения или законом Гаусса.

Эксперимент Муавра

Изучи информацию, представленную на изображении, и сделай вывод о функции плотности нормального распределения случайной величины.

Разделение материальных благ между субъектами экономических отношений. Первичное распределение обычно происходит в форме присвоения по праву собственности в процессе создания материального блага, в том числе с учётом разделения труда. Перераспределение происходит при передаче денег или иных благ от одних лиц к другим с помощью социальных механизмов, таких, как налогообложение, благотворительность, социальное обеспечение, земельные отношения, денежно-кредитная политика, конфискация, семейное право. Термин обычно относится к распределению дохода между факторами производства в экономике в целом, а не между отдельными лицами.

Эксперимент Муавра

Изучи информацию, представленную на изображении, и сделай вывод о функции плотности нормального распределения случайной величины.

В 1718 году в Лондоне вышла в свет книга под названием «Учение о случаях». Ее автор — французский математик А. Муавр. В своей книге Муавр описал свой эксперимент и сделал вывод.

Муавр измерил рост у 1375 случайно выбранных женщин и результат представил в виде диаграммы распределения роста женщин. Колоколообразная кривая, которая приближенно «накрывает» диаграмму распределения роста, похожа на смещенный направо график функции:

Эксперимент Муавра

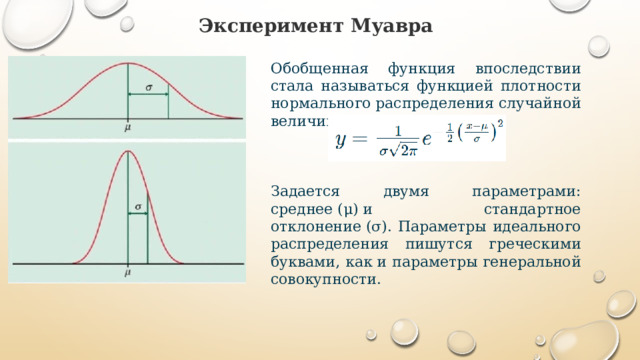
Обобщенная функция впоследствии стала называться функцией плотности нормального распределения случайной величины.

Задается двумя параметрами: среднее (μ) и стандартное отклонение (σ). Параметры идеального распределения пишутся греческими буквами, как и параметры генеральной совокупности.

Задача о спортивных костюмах

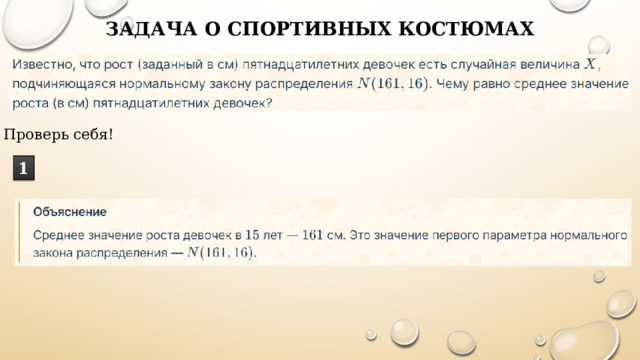
Проверь себя!

1

Задача о спортивных костюмах

Проверь себя!

Задача о спортивных костюмах

Проверь себя!

Задача о спортивных костюмах

Проверь себя!

Дополнительный материал

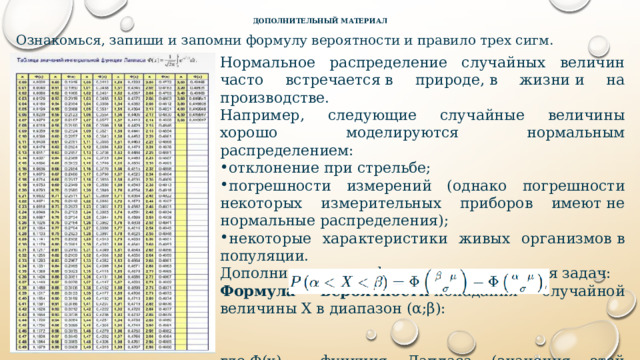
Ознакомься, запиши и запомни формулу вероятности и правило трех сигм.

Нормальное распределение случайных величин часто встречается в природе, в жизни и на производстве.

Например, следующие случайные величины хорошо моделируются нормальным распределением:

• отклонение при стрельбе;
• погрешности измерений (однако погрешности некоторых измерительных приборов имеют не нормальные распределения);
• некоторые характеристики живых организмов в популяции. 

Дополнительная информация для решения задач:

Формула вероятности  попадания случайной величины X в диапазон (α;β): 

где Φ(x) — функция Лапласа (значения этой функции берутся из таблицы).

Дополнительный материал

Ознакомься, запиши и запомни формулу вероятности и правило трех сигм.

Например, следующие случайные величины хорошо моделируются нормальным распределением:

• отклонение при стрельбе;
• погрешности измерений (однако погрешности некоторых измерительных приборов имеют не нормальные распределения);
• некоторые характеристики живых организмов в популяции. 

«Правило трех сигм»  справедливо для нормального распределения случайной величины: 

• в интервале (μ−σ,μ+σ) находится 68 % значений случайной величины;
• в интервале (μ−2σ,μ+2σ) находится 95,4 % значений случайной величины;
• в интервале (μ−3σ,μ+3σ) находится 99,7 % значений случайной величины.

Токарный станок

Проверь себя!

Токарный станок

Проверь себя!

Токарный станок

Проверь себя!

Токарный станок

Проверь себя!

Задача о подшипниках

Прочитай, продумай алгоритм, найди формулу и реши.

Шарикоподшипники в своей конструкции имеют такой основной элемент, как шарики. 

Благодаря высокому качеству исполнения данных деталей обеспечивается идеальная работа подшипников.

Шарики изготавливаются на специальном оборудовании различными способами. Они должны иметь идеально гладкую форму, так как это может сказаться на работе всего подшипника.

Задача

Станок изготавливает шарики для подшипников. Шарик считается годным, если отклонение X диаметра шарика от проектного размера по абсолютной величине меньше 0,5 мм. Считая, что случайная величина X распределена нормально со средним отклонением 0,25 мм, найди, сколько в среднем будет годных шариков среди ста изготовленных.

Интернет-ресурсы

https://edsoo.ru/