Элементы коучинга
Колесо баланса
Колесо баланса по теме: «Вычитание натуральных чисел», 5 класс
Данное колесо можно использовать на этапе рефлексии, если все темы изучены или при формулировании темы урока, если есть новые темы
Знание элементов вычитания (Уменьшаемое, вычитаемое, разность).
Вычитание многозначных чисел, где в составе уменьшаемого встречается много «0». (Например, 2000000-128935)
Применение первого свойства вычитания. (Если вычитаемое равно нулю, то разность равна уменьшаемому)
Применение второго свойства вычитания. (Если уменьшаемое и вычитаемое равны, то разность равна 0)
Решение текстовых задач на вычитание.
Применение третьего свойства вычитания – вычитания суммы из числа.
Применение четвертого свойства вычитания - вычитание суммы из числа.
Применение свойств вычитания для упрощения выражения.
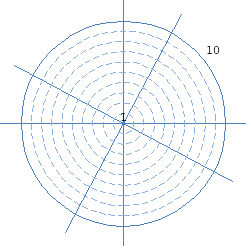
Колесо баланса по теме: «Сокращение дробей», 6 класс
Данное колесо можно использовать на этапе рефлексии.
Признаки делимости
Разложение чисел на простые множители
Запись произведения с помощью показателя степени
Поиск НОД
Основное свойство дроби
Сокращение дробей

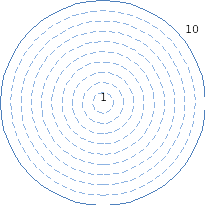
Колесо баланса по теме: «Умножение десятичных дробей», 5 класс
Данное колесо можно использовать на этапе рефлексии, если все темы изучены или при формулировании темы урока, если есть новые темы
Сложение целого числа и десятичной дроби;
Сложение десятичных дробей;
Вычитание из целого числа десятичной дроби;
Вычитание десятичных дробей;
Умножение целого числа на десятичную дробь;
Умножение десятичной дроби на 10, 100, 1000 и т.д.
Умножение десятичных дробей;
Умножение десятичных дробей на 0,1; 0,01; 0,001 и т.д.
Разработка коуч- сессий для обучающихся и педагогов по формату конечного результата и по логическим уровням.
Коуч- сессия по теме «Масштаб», 6 класс (для педагога)
| Постановка вопроса | Ответ |
| Чего ты хочешь? | Познакомить обучающихся с понятием Масштаб. Научить находить длину отрезка на местности, зная длину отрезка на карте и наоборот, используя масштаб карты. |
| Как ты узнаешь, что достиг результата? | По результатам домашней работы и самостоятельной работы или теста. Воспользуемся методикой Шкалирования. |
| В чём важность для тебя? | Важно, чтобы дети усвоили тему, чтобы смогли использовать её дальше на уроках географии и в жизни. Важно для повышения качества преподавания. |
| Как ты можешь этого достичь? | Провести практическую работу с картами и атласами. Провести измерения на местности, что бы «привязать к жизни», вызвать практический интерес. Показать, как решать такие задачи при помощи пропорции. |
Коуч-сессия по теме «Параллелограмм», 8 класс (для обучающихся)
| Постановка вопроса | Ответ |
| Чего ты хочешь? | Узнать, что такое параллелограмм и познакомиться с его свойствами, чтобы использовать их для решения задач. |
| Как ты узнаешь, что достиг результата? | Мне всё будет понятно и легко. Я буду его узнавать среди других фигур и с лёгкостью решать задачи. |
| В чём важность для тебя? | Мне важно научиться решать задачи, чтобы не было пробелов в знаниях; чтобы на следующий год успешно сдать экзамены. |
| Как ты можешь этого достичь? | Слушать учителя и самому попытаться разобраться в этом. Дома закрепить изученный материал. |
Коуч-сессия по теме «Зависимость между тригонометрическими функциями одного и того же аргумента», 10 класс (для педагога)
| Постановка вопроса | Ответ |
| Чего ты хочешь? | Ввести знаки тригонометрических функций числового аргумента; ввести основные тригонометрические формулы и закрепить их знание в ходе решения упражнений. |
| Как ты узнаешь, что достиг результата? | У ребят не будет вопросов при самостоятельном решении упражнений. |
| В чём важность для тебя? | Так эта тема водит в ЕГЭ, то владение ей в совершенстве для обучающихся просто необходимо. Поэтому для меня важно, чтобы они владели материалом. Это важно и для моего Я, смогла ли я научить этому. |
| Как ты можешь этого достичь? | Сначала буду использовать приём «корзина идей»: выслушав и записав все предположения десятиклассников, будем обсуждать эти все предположения, даже самые абсурдные. В результате исследования этих идей придем к нужному результату. Затем, выработать навык решения нужных упражнений и проверить правильность их решения. Ответь на вопросы, возникающие в ходе решения. |
Коуч- сессия по теме «Смежные и вертикальные углы», 7 класс (для педагога)
| Постановка вопроса | Ответ |
| Чего ты хочешь? | Создать условия для введения смежных и вертикальных углов, рассмотрение их свойств, введения понятия перпендикулярных прямых. |
| Как ты узнаешь, что достиг результата? | При проведении текущего контроля и выполнения заданий в рабочей тетради. При актуализации знаний на последующих уроках в форме устного опроса. Воспользуемся методикой «Колесо баланса» |
| В чём важность для тебя? | Эта тем является «базой» для решения последующих задач и в изучении тем по геометрии. |
| Как ты можешь этого достичь? | Сначала буду использовать приём «корзина идей»: выслушав и записав все предположения обучающихся. Проведем эксперимент, выполним практическую работу для того, чтобы прийти к свойствам смежных и вертикальных углов. |
Элементы кейс технологий
Кейс № 1. Округление чисел, 5 класс
Инструкция для учеников:
Прочитайте информационную статью «Округление чисел».
В тетради оформите решение Карточки 1.
Округление чисел (5 класс)
Один из трюков нашего мозга, чтобы облегчить работу с числами — округление. Наверняка все замечали на себе и окружающих, что мы питаем особое пристрастие к некоторым числам. Конечно, у всех это проявляется по-разному. Например, Илон Маск в своих инженерных проектах любит использовать особые числа из книги «Автостопом по Галактике»: именно поэтому на будущий корабль, который доставит первых колонистов на Марс планируют устанавливать 42 двигателя.
Но всё-таки у большинства обычных людей наиболее запоминающимися и простыми в использовании являются числа, которые заканчиваются на 5 и 0. Археологические исследования показали, что пристрастие к таким числам питают не только современные люди, но и представители древних цивилизаций, в том числе древние римляне и даже многие первобытные народы из разных частей света.
Несложно догадаться, что округление чисел до 5 и 0 связано с нашим использованием десятичной системы счисления. В свою очередь, десятичная система как наиболее естественная для человеческого мышления, основана на количестве пальцев на руках (две руки по пять пальцев).
Абстрактное мышление и операции с цифрами неестественны для мозга, а вот пальцы на руках — это наглядно, привычно и естественно. Таким образом, мозг может приспособить неестественную и трудную задачу, сведя её к простым и понятным манипуляциям. Именно поэтому людям свойственно округлять числа до 5 и 0.
Как замечает известный популяризатор науки Яков Перельман в своей книге «Занимательная арифметика», часто при переписи населения наблюдается чрезмерное обилие людей, возраст которых оканчивается на 5 или на 0; их гораздо больше, чем должно бы быть. Конечно, причина кроется в том, что люди не помнят твёрдо, сколько им лет, и невольно округляют свой возраст.
Что характерно, такое же округление возраста встречается на могильных камнях древних римлян. То есть там тоже чаще всего встречаются цифры 5 и 0 в обозначении возраста. Одно из научных исследований поставило целью определить популярность различных цифр в обозначении возраста на памятниках древних римлян и в надгробиях на кладбищах современного штата Алабама, населённого преимущественно чернокожим населением. Выяснилось удивительное соответствие. Частота повторяемости цифр возраста у древних римлян и современных негров совершенно одинакова. Цифры составляют одинаковую последовательность:
0, 5, 8, 2, 3, 7, 6, 4, 9 и 1
И дело не только в возрасте. Судя по всему, это чистая психология. В том же научном исследовании приводились результаты различных опытов, где людям предлагали определить «на глаз», сколько миллиметров заключает в себе полоска бумаги, например, в палец длиной. Опрос современных европейцев и анализ результатов выдал ту же самую последовательность:
0, 5, 8, 2, 3, 7, 6, 4, 9 и 1
Вряд ли это можно считать случайностью. Представители различных народов, люди разных эпох проявляют одинаковые пристрастия в выборе цифр.
Почему цифры 8 и 2 популярнее и удобнее для мозга, чем цифры 9 и 1? На этот вопрос нет однозначного ответа, хотя можно выдвигать разные версии. Очевидно только то, что цифры 5 и 0 связаны с удобным для мозга округлением чисел, в привязке к десятичной системе счисления.
Округление чисел происходит не только на подсознательном уровне. Некоторые дельцы умело манипулируют этой особенностью человеческого мышления. Например, при собеседовании на работу соискателю обычно предлагают зарплату, округлённую в большую сторону. Например, 100 000 вместо 95 000, потому что цифра 100 000 кажется более солидной и значительной, чем 95 000.
Продавцы товаров поступают в точности наоборот. Вместо цены товара $10 они указывают цену товара $9,99, которая подсознательно кажется менее значительной, чем $10.
Карточка 1.
Решите задачу.
Семья Цветочкиных собралась купить к лету земельный участок. Для экономии средств Валентина Павловна-мама- не захотела обращаться к риэлторам, и воспользовалась самым знаменитым сайтом в интернете, на котором без проблем можно было бы выбрать необходимый участок. Конечно, у каждого члена семьи к участку были свои требования- маме необходимо было наличие двух теплиц на участке размером 3 м на 6 м каждая, 7 грядок прямоугольной формы под цветы размером 2м на 2м, Валентину Федоровичу- папе- обязательное место отдыха в яблочном саду не менее 10м на 15м и домик, фундамент которого составлял бы не менее 100 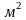 , а детям- место для игр и для установки бассейна площадью не менее 300
, а детям- место для игр и для установки бассейна площадью не менее 300 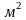 . За бюджет семьи отвечает Валентина Павловна, поэтому с пожеланиями папы она соглашаться отказывалась, но в тоже время не могла их совсем не учитывать, так как вся семья очень любила домашний яблочный сок и варенье из яблок. Так что ее задача - найти самое выгодное предложение такое, чтобы остались еще деньги на семена и на садовую утварь. Она нашла 3 объявления в интернете. Помогите маме из семьи Цветочкиных выбрать подходящий участок, так чтобы площадь желаемого участка не сильно отличалась от найденных в интернете.
. За бюджет семьи отвечает Валентина Павловна, поэтому с пожеланиями папы она соглашаться отказывалась, но в тоже время не могла их совсем не учитывать, так как вся семья очень любила домашний яблочный сок и варенье из яблок. Так что ее задача - найти самое выгодное предложение такое, чтобы остались еще деньги на семена и на садовую утварь. Она нашла 3 объявления в интернете. Помогите маме из семьи Цветочкиных выбрать подходящий участок, так чтобы площадь желаемого участка не сильно отличалась от найденных в интернете.
1 объявление- 10 соток, цена- 300 т.р.
2 объявление- 6 соток, цена- 210 т.р.
3 объявление- 7 соток, цена- 280 т.р.
Подходит конец 3 четверти и наступает пора выставления отметок. «Дневник.ру» в очередной раз не работает и Анна Васильевна столкнулась с проблемой – какую отметку поставить следующим ученикам, если известен их средний?
Васильев- 3,4
Кортунова- 4,3
Емельянов- 4,9
Савельев- 3,9
Помогите учителю с выставлением отметок.
Пользуясь решениями 1 и 2 задач сформулируйте правило округления десятичных дробей.
Кейс № 2. Площадь, 5 класс
Инструкция для учеников:
Рассчитайте, какой объем работы придется выполнить папе Леши Иванова
Сколько упаковок блоков уйдет на возведение дачного домика?
Выгодно ли заказчику воспользоваться услугами папы Леши или лучше выбрать сразу готовый дом при покупке дачного участка? (Для этого воспользуйтесь Сайтом «Авито», чтобы найти дачные домики приблизительно равной площади и узнать их стоимость)
Папа Леши Иванова занимается строительством. В его фирму поступил заказ, связанный со строительством дачи. Известны размеры дачного домика: ширина 5 метров, длина 8 метров. Заказчик попросил установить 2 окна размерами 1м * 2 м, дверь 2м *3 м и попросил, и сообщил, что уже залил фундамент прямоугольной формы. Папе Леши необходимо рассчитать объем расходуемого материла. Дом будет возводиться из блоков. Длина блока 50 см ширина- 20 см. Известно, что пачка, состоящая из блоков содержит 115 блоков и стоит 7000 рублей. За работу папа берет с заказчика 5000 рублей за возведение 1 квадратного метра. На возведение крыши необходимо -350 000 рублей. Какую сумму придется заплатить заказчику?
Кейс № 3. Десятичные дроби, 5 класс
Инструкция для учеников:
Прочитайте справочный материал «Происхождение дробей»
Выполните задания из Карточки 1
Заполните карточку «Задание 1»
Происхождение десятичных дробей. (5 класс)
К десятичным дробям математики пришли в разные времена в Азии и в Европе. Зарождение и развитие десятичных дробей в некоторых странах Азии было тесно связано с метрологией (учением о мерах). Уже во II в. до н. э. там существовала десятичная система мер длины.
Примерно в III в. н. э. десятичный счет распространился на меры массы и объема. Тогда и было создано понятие о десятичной дроби, сохранившей, однако, метрологическую форму. Вот, например, какие меры массы существовали в Китае в X в.: 1 лан=10 цянь=102 фэнь=103 ли=104 хао=105 сы=106 хо. Если вначале десятичные дроби выступали в качестве метрологических, конкретных дробей, десятых, сотых и т. д. частей более крупных мер, то позже они по существу стали все более приобретать характер отвлеченных десятичных дробей. Целую часть от дробной стали отделять особым иероглифом «дянь» (точка).В настоящее время целую и дробную часть принято разделять запятой. Однако в Китае как в древние, так и в средние века десятичные дроби не имели полной самостоятельности, оставаясь в той или иной мере связанными с метрологией. Более полную и систематическую трактовку получают десятичные дроби в трудах среднеазиатского ученого ал-Каши в 20-х годах XV в. Независимо от него, в 80-х годах XVI в. десятичные дроби были «открыты» заново в Европе нидерландским математиком С. Стевином.
В Средней Азии и в Европе ученые пришли к десятичным дробям по аналогии с шестидесятеричными и разработали теорию десятичных дробей.


ал Каши С.Стевин
Карточка 1. (1 группа)
Переведите миллиметры в сантиметры:
2 мм
5 мм
36 мм
Переведите китайские «Лан» в «Цянь»:
1 Лан
6 Лан
15 Лан
Сопоставьте дроби, записанные в левом столбце числовым значениям, записанным в правом столбце.
| Обыкновенная дробь | Десятичная дробь |
|
| 3,6 |
|
| 0,012 |
|
| 0,56 |
|
| 0,0135 |
|
| 0,5 |
Карточка 1. (2 группа)
Переведите сантиметры в дециметры:
5 см
8 см
15 см
Переведите копейки в рубли:
15 коп
89 коп
3 коп
Сопоставьте дроби, записанные в левом столбце числовым значениям, записанным в правом столбце.
| Обыкновенная дробь | Десятичная дробь |
|
| 5,4 |
|
| 0,12 |
|
| 0,026 |
|
| 0,0217 |
|
| 0,3 |
Карточка 1.( 3 группа)
Переведите дециметры в метры:
9дм
4 дм
11 дм
Переведите китайские «Лан» в «Цянь»:
3 Лан
2 Лан
22 Лан
Сопоставьте дроби, записанные в левом столбце числовым значениям, записанным в правом столбце.
| Обыкновенная дробь | Десятичная дробь |
|
| 7,5 |
|
| 0,089 |
|
| 0,13 |
|
| 0,0654 |
|
| 0,7 |
Карточка 1.(4 группа)
Переведите сантиметры в метры:
1 см
59 см
156 см
Переведите китайские «Лан» в «Цянь»:
9 Лан
7 Лан
75 Лан
Сопоставьте дроби, записанные в левом столбце числовым значениям, записанным в правом столбце.
| Обыкновенная дробь | Десятичная дробь |
|
| 3,4 |
|
| 0,45 |
|
| 0,097 |
|
| 0,0987 |
|
| 0,6 |
Задание 1. (Для всех групп)
Расскажите самые интересные факты, которые вам запомнились при прочтении сведений из истории математики.
Что в записи десятичной дроби отделяет целую часть от дробной?
Сколько цифр содержит запись дробной части десятичной дроби? От чего зависит количество цифр после запятой?
Назовите разряды целой и дробной частей в записи десятичной дроби.
| Целая часть | Дробная часть | ||||||
|
|
|
|
|
|
|
| |

 Получите свидетельство
Получите свидетельство Вход
Вход



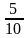
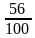
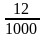
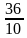
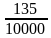
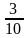
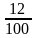
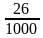
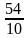
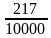
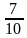
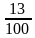
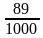
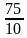
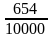
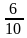
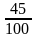
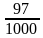









 Задания с элементами коучинга и кейс технологий. (147.96 KB)
Задания с элементами коучинга и кейс технологий. (147.96 KB)
 0
0 120
120 3
3 Нравится
0
Нравится
0


