Уровень А.
Логика – наука
о видах человеческой деятельности
о взаимодействии человека и природы
о взаимодействии между людьми
*о мышлении как средстве познания
Из каких частей состоит рассуждение ( исключить неверное)
Тезис
Доказательство
Вывод
*Отрицание
Понятие- это
*форма мышления, в которой отражаются существенные признаки предмета
форма мышления, в которой что-либо утверждается или отрицается
форма мышления, посредством которой из одного или нескольких суждений, по определенным правилам вывода получаем заключение
логическое мышление
Суждение-это
*форма мышления, в которой что-либо утверждается или отрицается
форма мышления, в которой отражаются существенные признаки предмета
форма мышления, посредством которой из одного или нескольких суждений, по определенным правилам вывода получаем заключение
логическое мышление
Форма мышления, посредством которой из одного или нескольких суждений выводится новое суждение
*Умозаключение
Аксиома,
Теорема,
Тезис
Решением какого уравнения не является рациональное число?
23х=6
452х+38=6
*251+х2 =1204
5х+57= 23
5+6=11 и 6+5 =11; 9+14 = 23 и 14+9 =23; значит от перестановки мест слагаемых сумма не меняется, это
Дедукция
Аналогия.
*Индукция
Силлогизм
Дедуктивное умозаключение с двумя посылками называется:
*Силлогизмом
Софизмом
Тезисом
Теоремой
Переход человека к пальцевому счету привел к созданию нескольких различных систем счисления. Самая древняя – пятеричная (пальцы одной руки), у индейских племен Северной Америки и Туземных обитателей Центральной и Южной Америки, а также в северной части Сибири и в Африке получила распространение двадцатеричная система счисления. У народов Европы преобладающей является эта система счисления?
*Десятеричная
Восьмеричная
Классическая
Европейская
Впервые эти числа были частично узаконены в Китае, а затем и в индии, где трактовались как долги (недостача). В Европе признание наступило на тысячу лет позже, да и то долгое время эти числа называли «ложными», «мнимыми» или «абсурдными». Немецкий математик Михаил Штифель дал определение этим числам, как чисел «меньше, чем ни чего». Как называются эти числа сейчас?
Дробные
Смешанные
Отрицательные*
Простые
С начала XVII века начинается интенсивное проникновение этих дробей в науку и практику. Сегодняшний вид этих чисел был предложен в 1617 году математиком Непером. О каких дробях идет речь?
Десятичные*
Обыкновенные
Рациональные
Бесконечные
Древнегреческие математики классической эпохи пользовались только целыми и дробными положительными числами. Эти числа объединяются в новое множество название которого происходит от латинского «ratio» – отношение, поэтому эти числа называют относительными. Как называются эти числа?
Вещественные
*Рациональные
Действительные
Иррациональные
Эти числа были открыты в пифагорейской школе при попытке соизмерить диагональ квадрата с его стороной. Греки называли это число словом «алогос» – невыразимое словами, европейские переводчики называли эту величину surodus – «глухой». Как эти числа называются сейчас?
Вещественные
Рациональные
Действительные
*Иррациональные
Все числа, которые есть на числовой прямой – рациональные и иррациональные – образуют новое множество чисел. обозначается оно буквой R, это обозначение происходит от английского слава «Real» – настоящий. Такой выбор неслучаен, потому что это множество включает в себя все числа, которые есть на числовой прямой. Как называется это множество?
Вещественные
Реальные
*Действительные
Мнимые
Эти числа были введены в математику для того, чтобы сделать возможной операцию извлечения квадратного корня из любого действительного числа. Как называются эти числа?
*Комплексные
Рациональные
Действительные
Иррациональные
Индийцы называли его словом "сунья", что значит пустой. Арабы - "никакой знак". Л. Магницкий в своей "Арифметике" называет "цифрой или ничем" (первая страница текста); на второй странице в таблице - "низачто". Как сегодня называется это понятие?
Минус
Плюс
Единица
*Нуль
Число делится на 9 ,если сумма цифр этого числа делится на 9. Сумма 1+2+9+8+7=27, 27/9=3, значит 12987 делится на 9. Это
*Дедукция
Аналогия
Индукция
Импликация
В высказывании «всякий прямоугольник является четырехугольником» . применяется квантор
существования
*общности
объединения
отклонения
Чтобы построить отрицание высказыванию с квантором общности, заменить его квантором существования. Чтобы построить отрицание конъюнкции, заменить его дизъюнкцией и наоборот. Союз «или» заменить на «и» . Этот метод называется:
Правилом Крамера
*Законом де Моргана
Теоремой Безу
Алгоритмом Евклида
Какое повествование не является высказыванием?
72 делится на 6.
Все числа делятся на 8.
Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны и равны.
*45+9
Если элементы множества А сопоставляются элементам множества В по определенному правилу, то это называется
Декартовым произведением множеств
*Соответствием множеств
Объединением множеств
Пересечением множеств
22. Понятия, в которых мыслятся признаки некоторой совокупности предметов, составляющих единое целое:
соотносительные
конкретные
общие
*собирательные
23. Подмножеством любого другого множества является
*пустое множество
универсальное множество
нет правильных ответов
24. Логический термин «квантор общности» соответствует слову
* все
некоторый
существует
каждый
25. Если a b, тогда
a c
*a
a = c
26. Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский, арабский. На вопрос, какой язык изучает каждый из них, прозвучали перечисленные ответы: Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Выберите верное утверждение.
Вадим изучает китайский
Сергей не изучает китайский
*Михаил не изучает арабский
27. Укажите верное утверждение:
Линейной функцией называется выражение вида ax + b, где a, b – переменные, x – число.
Число 144 оканчивается цифрой 1.
Равенство, содержащее неизвестное число, называется уравнением.
*Корнем уравнения называется число, при подстановке которого в уравнение, вместо переменной, получается верное равенство.
УРОВЕНЬ В.
Найти произведение суммы и разности рациональных чисел 5,3 и 1,2. Ответ: 26,65
Найти количество элементов в пересечении множеств А= {2,5,18,29} и В={12,15,18,29,30,45}. Ответ: 7
Найти количество элементов в пересечении множеств С= {а,б,к,р} и У={ф,а,т,и,м}. Ответ: 1
Найти количество элементов в пересечении множеств Х= {3,5,7,9,11} и Е={2,4,6,8,10}. Ответ: 0
Найти количество элементов в объединении множеств А= {10,20,30,40} и В={20,30,40,50}. Ответ: 5
Найти количество элементов в объединении множеств К= {ч,а,с,ы} и Т={в,р,е,м,я}. Ответ: 7
Найти количество элементов в объединении множеств R= {25,35,45,55} и W={25,35,45,55}. Ответ: 4
Чему равно количество элементов в разности множеств Н= {1,2,3,4,5,6} и С={1,2,3}. Ответ: 3
Чему равно количество элементов в разности множеств Х= {а,б,в,г,д} и У={а,б,в,г}. Ответ: 1
Чему равно количество элементов в разности множеств А= {24,34,54,64} и М={24,34,54,64}. Ответ: 0
Вычисли количество элементов в декартовом произведении множеств В= {5,6,7,8} и Н={2,3,4,5}. Ответ: 16
Вычисли количество элементов в декартовом произведении множеств К= {3,13,23} и Х={25,35}. Ответ: 6
Вычисли количество элементов в декартовом произведении множеств С= {7,17} и У={100,200}. Ответ: 4
Решить уравнение на множестве рациональных чисел 4х + 38=6. Ответ: 8
Чему равно произведение последовательных целых чисел, - начинающихся числом -5 и оканчивающихся числом 5? Ответ: 0
Решить уравнение на множестве рациональных чисел
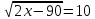 . Ответ:95
. Ответ:95Решить уравнение на множестве положительных действительных . В ответе указать положительный корень. 2х2 + 9 = 81. Ответ:6
Найти сумму произведения и частного целых чисел -48 и 12. Ответ: 580
Если множество содержит 3 различных элемента. Количество подмножеств данного множества равно. Ответ: 6
Сколько элементов содержат следующее множество: {{у},у,а,{а}} - Ответ: 4
Совпадают ли множества {8,9,6} и {9,8,6}? Ответ: Да
Дано множество С= {1, 2, 4}. Сколько подмножеств у данного множества С? Ответ: 8
Дано множество А= {7,11, 16, 20,27}. Сколько подмножеств у данного множества А? Ответ: 32
Дано множество У= {м,а,т,е,к}. Сколько подмножеств у данного множества А? Ответ: 16
Являются ли множества А и В равносильными? А= {2,7,9,11} и В={11,9,7,2}. Ответ: да
Сколько столбцов будет у этого высказывания (А↔В) ᶺ (АᶺВ), при построении таблицы истинности. Ответ: 5
Сколько строк будет у этого высказывания (АᶺВ) ᶺ (А→В) при построении таблицы истинности. Ответ: 4
Сколько столбцов будет у этого высказывания (АᶺВ) ᶺ (А→В) при построении таблицы истинности. Ответ: 5
Сколько строк будет у этого высказывания АᶺВ при построении таблицы истинности. Ответ: 4
Сколько столбцов будет у этого высказывания АᶺВ →В при построении таблицы истинности. Ответ: 4
Сколько строк будет у этого высказывания (АᶺВ) ᶺ А→ С при построении таблицы истинности. Ответ: 8
Два теплохода одновременно вышли из портов и с постоянной скоростью движутся во встречном направлении. Скорость одного теплохода 20 км/час, другого – 30 км/час. На каком расстоянии друг от друга они будут находиться ровно за один час до их встречи? Ответ: 50
Является ли истинным данное высказывание(∃x):x +1 Ответ: да
35 учеников зарегистрированы в школьной или городской библиотеках. Из них 25 регулярно посещают школьную библиотеку, а 20 – городскую. Сколько учеников посещают обе библиотеки? Ответ: 10
Продолжить последовательность
1
11
21
1211
111221... Ответ: 312211
Проверить истинно ли данное высказывание : Произведение чисел 4070 и 8 меньше, чем сумма чисел 18396 и 14174. Ответ: да
Укажите количество двухэлементных подмножеств множества А ={2,6,3,9} . Ответ: 6
Даны числа: 31,53,409,348,20,3094,233,33,271,143,3,333,14,30. Укажите количество чисел, в записи которых: три цифры и есть цифра 3. Ответ: 4
Выяснить закономерность в данной последовательности. Какое число должно быть на месте вопросительного знака?
629 = 2
1298 = 3
888 = 6
100 = 2
7890 = 4
36698 = ?
Ответ: 5Выяснить закономерность в данной последовательности. Какое число должно быть на месте вопросительного знака?
100 = 2
210 = 1
360 = 2
480 = 3
590 = 2
690 = ?
Ответ: 4Даны числа: 3,37,210,48,56,63,75,89,120,453,33,596,734. Укажите количество чисел, в записи которых две цифры или есть цифра 3. Ответ: 10
Даны числа: 41,54,409,348,50,394,42,59,271,143,4,555,58,40. Укажите количество чисел, в записи которых три цифры или есть цифра 4. Ответ:9
Найдите количество элементов в пересечении множеств А и В если А={26,39,5,58,17,81} B={2,6,3,9,1,7} . Ответ: 0
Найти количество элементов в разности множеств А и В, если: А={а,в,с,d,e,s}, В={x,f,s,e,t,y} Ответ: 4
Уровень С.
У Милены на телефоне тариф «Переходи на ноль», по которому она может разговаривать в день 30 минут на мегафоне по Северному Кавказу бесплатно, а каждая следующая минута тарифицируется по 2 рубля ежеминутно. На счету у Милены сегодня было 3 руб. после разговора 50 мин какая сумма окажется у нее на счету? Ответ: -37
Решить задачу, используя диаграмму Эйлера-Венна.
Четырнадцать спортсменов участвовали в кроссе, 16 – в соревнованиях по плаванию, 10 – в велосипедных гонках. Восемь участников участвовали в кроссе и заплыве, 4 – в кроссе и велосипедных гонках, 9 – в плавании и велосипедных гонках. Во всех трех соревнованиях участвовали три человека. Сколько всего было спортсменов? Ответ: 22В классе 35 учеников. Каждый из них пользуется хотя бы одним из видов городского транспорта: метро, автобусом и троллейбусом. Всеми тремя видами транспорта пользуются 6 учеников, метро и автобусом – 15 учеников, метро и троллейбусом – 13 учеников, троллейбусом и автобусом – 9 учеников. Сколько учеников пользуются только одним видом транспорта? Ответ: 10
В лицее учится 72 ученика 6 классов. Из них 50 человек увлечены математикой, 40 ребят – информатикой, а 10 человек не увлечены ни тем, ни другим. Сколько учеников увлечены и математикой и информатикой сразу? Ответ: 28
Заполните таблицу истинности
| А | В | А→В | А↔В | (А→В) ᶺ (А↔В) |
| 1 | 1 | | | |
| 1 | 0 | | | |
| 0 | 1 | | | |
| 0 | 0 | | | |
Ответ:
| А | В | А→В | А↔В | (А→В) ᶺ (А↔В) |
| 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
Заполните таблицу истинности
| А | В | АᶺВ | А↔В | (АᶺВ) ᵥ(А↔В) |
| 1 | 1 | | | |
| 1 | 0 | | | |
| 0 | 1 | | | |
| 0 | 0 | | | |
Ответ:
| А | В | АᶺВ | А↔В | (АᶺВ) ᵥ(А↔В) |
| 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
Заполните таблицу истинности
| А | В | АᵥВ | А→В | (АᵥВ) ᶺ (А→В) |
| 1 | 1 | | | |
| 1 | 0 | | | |
| 0 | 1 | | | |
| 0 | 0 | | | |
Ответ:
| А | В | АᵥВ | А→В | (АᵥВ) ᶺ (А→В) |
| 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 |
Кружок по математике проходит через каждые 5 дней, по информатике – через каждые 4 дня, по английскому – через каждые 8 дней. Через какое наименьшее количество дней кружковцы встретятся в здании, если занятия у них начинались в один день? Ответ: 40
В лицее учится 72 ученика 6 классов. Из них 50 человек увлечены математикой, 40 ребят – информатикой, а 10 человек не увлечены ни тем, ни другим. Сколько учеников увлечены и математикой и информатикой сразу? Ответ: 28
В деревне в каждой семье есть козы или куры, причем в 22 дворах есть козы, а в 26 дворах – куры. В 16 дворах есть сразу и коровы и куры. Сколько в этой деревне дворов? Ответ: 32
Первый кусок проволоки на 54 м длиннее второго. После того, как от каждого куска отрезали по 12м, второй кусок оказался в 4 раза короче первого. Найти первоначальную длину первого куска. Ответ: 14
Ручка в 2 раза дороже карандаша, а резинка в 3 раза дешевле карандаша. Ручка, карандаш, резинка вместе стоят 400р. Сколько стоит резинка? Ответ: 40
На одной полке на 6 книг больше ,чем на другой. Сколько книг нужно переложить с одной полки на другую, чтобы книг стало поровну? Ответ: 3
На одной полке на 6 книг больше ,чем на другой. На сколько книг будет на первой полке больше, если со второй полки переложить на первую 10 книг? Ответ: 26
В двух бидонах 28 литров краски. Если из первого бидона взять 3л, а в другой добавить 2л, то в первом станет на 7 литров краски больше, чем во втором. Сколько краски станет во втором бидоне? Ответ : 10
Игорь и Паша красят забор за 20 часов. Паша и Володя красят этот же забор за 24 часа, а Володя и Игорь – за 30 часов. За сколько минут мальчики покрасят забор, работая втроем? Ответ: 960
Даны множества А={1, 2} и В={a, b}. Из скольких элементов состоит декартовое произведение A×B Ответ: 4
13

 Получите свидетельство
Получите свидетельство Вход
Вход












 Зачетные вопросы по дискретной математике с ЭМЛ (44.23 KB)
Зачетные вопросы по дискретной математике с ЭМЛ (44.23 KB)
 0
0 881
881 21
21 Нравится
0
Нравится
0


