Муниципальное бюджетное общеобразовательное учреждение
«Красногвардейская школа №1»
ЗАЧЕТЫ ПО АЛГЕБРЕ И НАЧАЛАМ АНАЛИЗА. 11 КЛАСС.
(Дифференцированный подход)
Составитель:
Коваленко Инна Николаевна-
учитель математики
2015г.
Пояснительная записка
Урок обобщения и систематизации знаний и умений имеет большое обучающее и воспитывающее значение для учащихся. Одна из форм такого урока-зачет.
Для достижения высоких результатов обучения и прочного усвоения знаний желательно проводить зачеты после каждой большой темы или раздела программы. Подготовка к зачетам должна начинаться с первого урока новой темы.
Во время зачета учащимся предлагается выполнить следующую работу:
1. Ответить на 2 теоретических вопроса устно или письменно.
2. Решить 2 задачи.
Задания предлагаются дифференцированно, с учетом индивидуальных особенностей каждого ученика. Ответы на задания из группы «А» оцениваются в три балла, группы «В» - в четыре балла, группы «С» - в пять баллов.
Получив задание, учащийся выполняет его письменно, а затем сдает учителю, который тут же проверяет и объявляет оценку.
Оценивание:
За каждый теоретический вопрос-2 б
За каждое практическое задание – в зависимости от выбранного уровня.
Отметка «5» - 15-16 баллов.
Отметка «4» - 12-13-14 баллов.
Отметка «3» - 9-10-11 баллов.
Зачет по теме:
«Производная и её применение»
Теоретические вопросы:
Приращение функции и аргумента.
Определение производной.
Геометрический и физический смысл производной.
Мгновенная скорость.
Таблица производных элементарных функций.
Правила вычисления производных (производная суммы,
разности, произведения и частного).
Производная сложной функции.
Непрерывность функции. Метод интервалов.
Критические точки функции.
Стационарные точки.
Точки перегиба.
Точки экстремума функции.
Необходимое и достаточное условие существования
экстремума функции.
Наибольшее и наименьшее значение функции.
Уравнение касательной функции.
Признак возрастания и убывания функции.
Приближенные вычисления.
Исследование функции с помощью производной.
Задачи
Уровень А
–каждое задание оценивается в 3 балла
Найдите приращение функции в точке х0, если f(x)=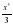 ; х0=3; Δх =0,1.
; х0=3; Δх =0,1.
Вычислите значение производной функции f(x) = 4x7+6x4+10x при х=1.
Решите неравенство f'(x)0, если f(x)=-6x2-15x.
Вычислите производную функции f(x)=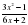
Найдите значение производной функции при заданном значении аргумента, если f(x)=2 tg x; x0=0.
Решите уравнение: f'(x)=0, если f(x)=-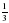 x3+4х2-9x.
x3+4х2-9x.
Вычислите в точке х0, если f(x)=15x2-7, х0=2, Δх =0,5.
Вычислите значение производной функции f в данной точке, если
f(x)=2х ∙ cosx; x0=0.
Найдите значения х, при которых производная функции f равна нулю, если f(x)=2 x4-16х3.
Решите неравенство (3х-6)(2х+4) ≥ 0.
Найдите область определения функции f(х) = 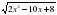 .
.
Точка движется прямолинейно по закону х (t) = 6t3+2t-3. Найдите скорость в момент времени t= 2 с.
Найдите промежутки возрастания функции f(х) = 7х2-8х+3
Найдите критические точки функции f(х) = 8х3-5х2-4.
Определите, какие из них являются точками максимума, а какие – точками минимума.
Докажите, что функция f(х) = 6х5+4х не имеет критических точек.
Найдите промежутки убывания функции f(х) = 4+16х-х
Напишите уравнение касательной к графику функции f(х) = х3-6 в точке с абсциссой х0 = -1
Найдите тангенс угла наклона к оси абсцисс касательной, проходящей через данную точку А (1;2) графика функции f(х) = х2+4х
Уровень В
-каждое задание оценивается в 4 балла
Найдите мгновенную скорость точки, движущейся по закону х (t)=t2-4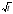 , в момент времени t0=4.
, в момент времени t0=4.
Найдите f'(x), f'(-2), если f(x) = (2+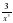 )(x-2).
)(x-2).
Решите неравенство f'(x)0, если f(x)=sin2x.
Найдите производную данной функции f(x)=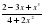 . Вычислите
. Вычислите
2f'(-2)+3f (1).
Вычислите значение производной функции при заданном значении аргумента, если f(x)= (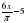 )∙ ctgx; x0=
)∙ ctgx; x0=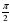 .
.
Составьте и решите уравнение: f'(x)= f(x) – 3х, если f(x)=3х+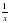 .
.
Найдите производную функции f(x)=(2-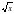 )∙tg2x.
)∙tg2x.
Решите уравнение f'(x)=0, если f(x)=1,5sin2x-5sinx-x.
Докажите, что при всех допустимых значениях х производная функции g(x) не может принимать отрицательных значений, если: g(x)=tg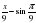 .
.
Вычислите приближенное значение 1,005100.
На графике функции g(х) =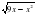 найдите точку, в которой касательная к графику параллельна оси абсцисс.
найдите точку, в которой касательная к графику параллельна оси абсцисс.
Найдите угловой коэффициент касательной к графику функции
f(х) = (х2+2)(х3-3), в точке х0 = 2.
Найдите точки экстремума функции f(х) = (х+1)2(х+5)2.
Найдите критические точки функции f(х) = sin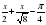 .
.
Колесо вращается так, что угол поворота пропорционален квадрату времени. Первый оборот был сделан колесом за 6 с. Найдите угловую скорость через 40с после начала вращения.
Найдите наибольшее значение функции f(х) = (х+1)2(х+4) на данном промежутке [-5;0]
Исследуйте функцию у= 2х2+3х-5 и постройте её график.
При каких значениях n функция f(х) =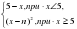 непрерывна на всей числовой прямой.
непрерывна на всей числовой прямой.
Уровень C
- каждое задание оценивается в 5 баллов
Найдите корни уравнения f '(x)=0, принадлежащие отрезку [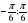 ], если f(х) = cos (
], если f(х) = cos (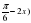 .
.
Найдите производную функции f(x) = , в точке х0=
, в точке х0=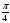 .
.
Укажите, какой формулой можно задать функцию у= f(x), если
f '(x)=-20 (4-5х)3.
Найдите точки, в которых f '(х)=0, f '(x)0, если f (x)=4x+cos (4x- ).
).
Найдите значения аргумента, удовлетворяющие условию f '(х)=g' (x), если f(x)= 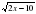 , g (x) =
, g (x) =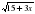 .
.
Найдите производную функции у=tg(3x-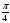 ), в точке х0=
), в точке х0=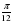 .
.
Дано: f(x) = csin2x+ d cosx, f '(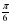 )= 4; f '(
)= 4; f '( )=-8. Чему равны c и d?
)=-8. Чему равны c и d?
Вычислите скорость изменения функции у= cos ( ) в точке х0=
) в точке х0= .
.
При каких значениях х выполняется равенство f '(х)=2, если известно, что
f (х)=2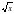 -5
-5 ?
?
Исследуйте функцию и постройте её график: у =  .
.
Среди всех равнобедренных треугольников с боковой стороной 5 см найдите треугольник наибольшей площади.
Исследуйте функцию у=х2 и постройте её график.
и постройте её график.
Найдите точки экстремума функции f(х) = cos 2х+2sin х .
Известно, что наименьшее значение функции f(х) = 3х2-х3 на промежутке
[-2; в] равно нулю. При каком максимальном значении выполняется это
условие?
Составьте уравнение касательной к графику функции f(х) = , если её угловой коэффициент равен к=
, если её угловой коэффициент равен к= .
.
Примеры решения задач по теме: «Производная»
1). Найдите приращение функции в точке х0, если f(x)= ; х0=1; Δх =0,1.
; х0=1; Δх =0,1.
Решение:
1. Находим значение х0+Δх: х0+Δх=1+0,1=1,1
2. Вычисляем значение f(x0): f(1)=
3.Вычисляем значение f(x0+Δх): f(1,1)=
4. Находим приращение функции Δf(x): Δf(x)= f(1,1)- f(1)=0,605- 0,5=0,105
Ответ: Δf(x)=0,105
2). Вычислите значение производной функции f(x) = 8x6+5x3+12x при х=1.
Решение:
1. f '(x) = (8x6)' +(5x3)' +(12x)'=8∙6х5+5∙3х2+12∙1=48х5+15х2+12
2. f '(1)= 48∙15+15∙12+12=75
Ответ: 75
3). Решите неравенство f '(x)0, если f(x)= -10x2-17x.
Решение:
1. f '(x)=(-10x2)'- (17x)'= -10∙2х-17∙1= -20х-17
2. f '(x)0, -20х-170, -20х 17, х
Ответ: f '(x)0, при х.
4). Вычислите производную функции f(x)=
Решение:
f '(x)==
5). Найдите значение производной функции при заданном значении аргумента, если f(x)=5 tgx, x0= .
.
Решение:
1. f '(x)=( 5 tgx)'=5∙
2. f '( )=5∙
)=5∙
Ответ: f '( )=20
)=20
6). Решите уравнение: f '(x)=0, если f(x)= x3+
x3+ х2-3x.
х2-3x.
Решение:
1. f '(x)=( x3)'+(
x3)'+( х2)'-(3x)'=
х2)'-(3x)'= ∙3x2+
∙3x2+ ∙2х-3∙1=2х2+х-3
∙2х-3∙1=2х2+х-3
2. f '(x)=0, 2х2+х-3=0, D= в2-4ас=12-4∙2∙ (-3)=25,
х1=
х2=
Ответ: f '(x)=0, при х = -1,5; 1
7). Вычислите значение производной функции в данной точке, если
f (x)=3х∙sin x, x0=0
Решение:
1. (u∙v)'=u'∙v + u∙v'
f '(x)=(3x)' sin x + 3x ∙(sin x)' = 3 ∙sin x + 3x ∙ cos x
2. f '(0)= 3∙ sin 0 + 3∙ 0 ∙cos 0 = 3 ∙0 + 0 ∙1 = 0
Ответ: f '(0)= 0
Примеры решения задач по теме «Применение производной»
1). Решите неравенство (4х-6)(5х+10) ≥ 0.
Решение:
1. Рассмотрим функцию у= (4х-8)(5х+10)
2. Найдем нули функции: у=0, (4х-8)(5х+10) = 0, 4х-8=0 или 5х+10=0

 4х=8 5х=-10
4х=8 5х=-10
 + _ +
+ _ +
 3.
3.  """"∙ ∙""""" х
""""∙ ∙""""" х
-2 2
Ответ: ( ],
], 
2). Найдите область определения функции f(х) =  .
.
Решение:
1. Решим неравенство: 2х2+х-3≥ 0
2. Рассмотрим функцию у=2х2+х-3 и найдем ее нули:
2х2+х-3=0, D= в2-4ас=12-4∙2∙ (-3)=25,
х1=
 х2=
х2=

 + - +
+ - +
 3.
3.  """"∙ ∙""""" х
""""∙ ∙""""" х
-1,5 1
Ответ: ( ],
], 
3). Точка движется прямолинейно по закону х (t) = 5t3+30t-7 (м). Найдите скорость в момент времени t= 1 с.
Решение:
1. v(t)= х '(t) =(5t3+30t-7)'=5∙3t2+30∙1-0=15 t2+30
2. v(1)= 15 ∙12+30= 45 (м/с)
Ответ: v(1)= 45 м/с.
4). Найдите промежутки возрастания и убывания функции f(х) = 10х2-2х+1
Решение:
1. Область определения функции: D(f)=R
2. Найдем производную функции: f '(х) = (10х2-2х+1)'=10∙2х-2∙1+0=20х-2
3. Решим неравенства: а) f '(х)0, б) f '(х)
20х-20 20х-2
20х2 20х
х  х
х
Ответ: функция f(х) = 10х2-2х+1 возрастает при х  , убывает при х .
, убывает при х .
5). Найдите критические точки функции f(х) = 5х3+3х2-1
Определите, какие из них являются точками максимума, а какие – точками минимума.
Решение:
1. Найдем производную данной функции: f (х) = (5х3+3х2-1)'=
=5∙3х2+3∙2х-0=15х2+6х


 2. Найдем критические точки: f '(х)=0, 15х2+6х=0, 3х (5х+2)=0, х=0 или 5х+2=0, 5х = -2, х = -0,4
2. Найдем критические точки: f '(х)=0, 15х2+6х=0, 3х (5х+2)=0, х=0 или 5х+2=0, 5х = -2, х = -0,4
+ - +



 3.
3.  """"∙ ∙""""" х
""""∙ ∙""""" х
-0,4 0
max min
Ответ: хmax= -0,4, xmin=0.
6). Напишите уравнение касательной к графику функции f(х) = 3х3+4 в точке с абсциссой х0 = 2.
Решение:
1. Найдем у0= f (х0): f(2)= 3∙23+4=28
2. Найдем f '(х): f '(х)= (3х3+4)'=3∙3х2+0=9х2
3.Найдем f '(х0): f '(2)=9∙22=36
4. Подставим полученные результаты в уравнение касательной:
у= у0 + f '(х0)∙ (х-х0):
у=28+36(х-2), у=28+36х-72, у=36х-44- искомое уравнение касательной.
7). Найдите тангенс угла наклона к оси абсцисс касательной, проходящей через данную точку А (2;-3) графика функции f(х) =х3+2х.
Решение:
1. Найдем производную: f '(х) =(х3+2х)'=3х2+2
2. Найдем f '(х): f '(2)= 3∙22+2=14
3. tg = f '(2)=14
= f '(2)=14
Ответ: 14
Литература.
1. Алгебра и начала математического анализа 10 класс. Учебник. Базовый и профильный уровни Никольский С.М. и др. 8-е изд. - М.: Просвещение, 2009.
2. А.П. Ершова, В.В. Голобородько. Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 классов.
3.Ю.А. Глазков, И.К. Варшавский, М.Я. Галашвили. Тесты по алгебре и началам анализа. 10 класс. Издательство «Экзамен». Москва,2010.


 Получите свидетельство
Получите свидетельство Вход
Вход



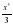 ; х0=3; Δх =0,1.
; х0=3; Δх =0,1.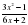
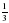 x3+4х2-9x.
x3+4х2-9x.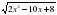 .
.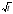 , в момент времени t0=4.
, в момент времени t0=4.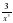 )(x-2).
)(x-2).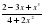 . Вычислите
. Вычислите 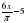 )∙ ctgx; x0=
)∙ ctgx; x0=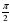 .
.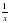 .
.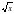 )∙tg2x.
)∙tg2x.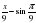 .
.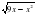 найдите точку, в которой касательная к графику параллельна оси абсцисс.
найдите точку, в которой касательная к графику параллельна оси абсцисс.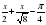 .
.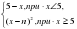 непрерывна на всей числовой прямой.
непрерывна на всей числовой прямой. 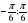 ], если f(х) = cos (
], если f(х) = cos (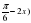 .
. , в точке х0=
, в точке х0=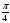 .
. ).
).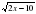 , g (x) =
, g (x) =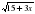 .
.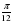 .
.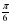 )= 4; f '(
)= 4; f '(








 Зачет по алгебре и началам анализа "Производная и её применение" (0.12 MB)
Зачет по алгебре и началам анализа "Производная и её применение" (0.12 MB)
 1
1 3722
3722 570
570 Нравится
0
Нравится
0


