
УПРАВЛЕНИЕ ОБРАЗОВАНИЯ И НАУКИ ЛУГАНСКОЙ ОБЛАСТНОЙ ГОСУДАРСТВЕННОЙ АДМИНИСТРАЦИИ
КУ "ЛУГАНСКАЯ ОБЛАСТНАЯ МАЛАЯ АКАДЕМИЯ НАУК УЧАЩЕЙСЯ МОЛОДЕЖИ"
автор – составитель : А. С. Воронкин
ВОЛНОВЫЕ ПРОЦЕССЫ
Луганск - 201 3

ТЕМА III .
ВОЛНОВЫЕ ПРОЦЕССЫ
План
3.1 . Волновой процесс
3 . 2. Демонстрация волнового движения: связанные маятники и волновые машины
3 . 3. Поперечные, продольные и поверхностные волны
3.4. Связь между длиной волны, скоростью ее распространения и периодом
3.5. Волновая поверхность
3 . 6 . Смещение частиц среды в бегущей волне
3 . 7 . Поток энергии и интенсивность волны. Вектор Умова
3.8. Понятие о линейных и нелинейных волнах

3.1 . Волновой процесс
Пожалуй, самыми наглядными являются волны на поверхности воды. Их можно просто увидеть невооруженным взглядом.
Бросим камень, скажем, в озеро со спокойной поверхностью воды. От места падения камня начнет распространяться волна, а вернее целая “ группа волн ”.
Волны, идущие по поверхности воды от брошенного камня, являются круговыми
Наблюдается сумма колебаний различных частот и обнаруживается изменение амплитуды во времени.
Итак, при распространении некоторого волнового импульса мы наблюдаем распространение нескольких волн (некоторой их группы). Скорость распространения импульса потому и называется групповой .
Количество синусоидальных волн, образующих импульс (волновой пакет, группу волн, цуг) может быть как конечным (минимум – две), так и бесконечным.

Точечный источник волн
Чтобы получить круговые волны на поверхности воды нам необходимо создать некоторое возмущение в точке, которая будет центром окружностей, образованных фронтами.
Чтобы эта волна имела определенную (единственную) частоту необходимо непрерывное (периодическое) возмущение. Его можно осуществить с помощью колеблющегося в вертикальном направлении закрепленного на стержне шарика подходящих размеров. Хотя и такая волна все-таки не будет синусоидальной, так как ее амплитуда будет обратно пропорциональной корню квадратному от расстояния до начала координат .
В Н И М А Н И Е
Причиной возникновения волны является не само движение шарика, а периодическое возмущение поверхности воды в точке возникновения волны.

Волновой процесс
При рассмотрении колебаний можно не учитывать некоторые особенности среды, в таком случае среда рассматривается как сплошная , непрерывно распределенная в пространстве и обладающая упругими свойствами .
Волновым процессом или волной называется процесс распространения колебаний с конечной скоростью в сплошной среде.
При распространении волны частицы колеблются около своих положений равновесия, а не перемещаются вслед за волной .
Основным свойством всех волн является перенос энергии без переноса вещества .
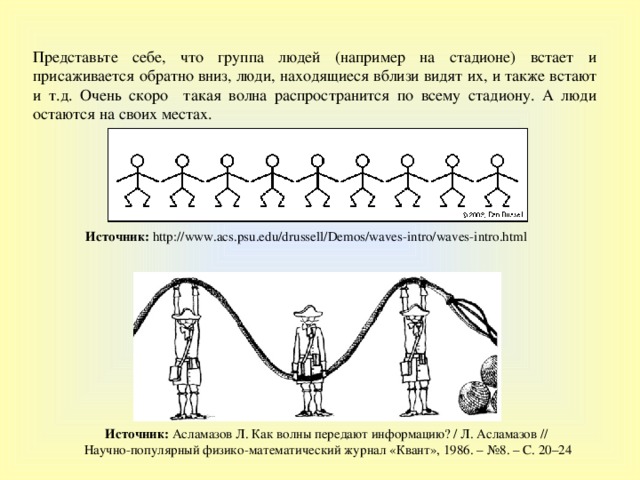
Представьте себе, что группа людей (например на стадионе) встает и присаживается обратно вниз, люди, находящиеся вблизи видят их, и также встают и т.д. Очень скоро такая волна распространится по всему стадиону. А люди остаются на своих местах .
Источник : http://www.acs.psu.edu/drussell/Demos/waves-intro/waves-intro.html
Источник : Асламазов Л. Как волны передают информацию? / Л. Асламазов //
Научно-популярный физико-математический журнал «Квант», 1986. – №8. – С. 20–24

3.2 . Демонстрация волнового движения: связанные маятники и волновые машины
Волновые процессы удобно изучать на примере связанных маятников , которые являются основой так называемых волновых машин.
Для демонстрации прикрепим два идентичных математических маятника (с одинаковыми грузиками и нитями одной длины) к поперечному гибкому подвесу (нити), концы которого жестко закреплены в штативах. Математические маятники расположим симметрично друг от друга.
Удерживая один из маятников в положении равновесия, другой отклоним на небольшой угол в поперечном направлении. Будем наблюдать за поведением маятников. Амплитуда колебаний первоначально отклоненного маятника будет постепенно уменьшаться, одновременно с этим второй маятник будет раскачиваться сильнее и сильнее. В какой-то момент времени маятники будут колебаться с одинаковыми амплитудами.

Спустя некоторое время первый маятник приостановится (т.е. войдет в первоначальное состояние равновесия), а второй раскачается настолько, что его амплитуда будет примерно такой же, как в начальный момент у первого маятника. Продолжим наблюдать. Теперь все процессы будут происходить в обратной последовательности – амплитуда второго маятника будет уменьшаться, а первого – увеличиваться (до тех пор, пока не достигнет прежней амплитуды). Затем все повторится сначала.
Результат, полученный на конкретном примере, имеет общий характер: в связанных колебательных системах колебательное возбуждение распространяется .
Для демонстрации механизма образования продольных и поперечных волн в середине XIX века начали появляться так называемые волновые машины. Одна из таких модификаций, созданная Эбенизерем Стронгом Снеллом представлена на рис. справа

На следующем рисунке представлена одна из демонстрационных модификаций волновой машины.
Ряд бифилярно подвешенных маятников также могут колебаться перпендикулярно к оси ряда. Если последовательно выводить маятники из положения равновесия (что достигается равномерным движением наклонной пластинки, показанной в правой части рисунка), то создается модель бегущей волны.
ВНИМАНИЕ
Каждая частица (в данном случае грузик) колеблется около своего положения равновесия значительно быстрее , чем распространяется сама волна. В зависимости от направления колебаний частиц и направления распространения волны различают волны поперечные и продольные .
3.3 . Поперечные, продольные и поверхностные волны
Внутри твердых, жидких и газообразных сред могут распространяться упругие волны. В зависимости от направления колебаний частиц и направления распространения волны различают волны поперечные и продольные .
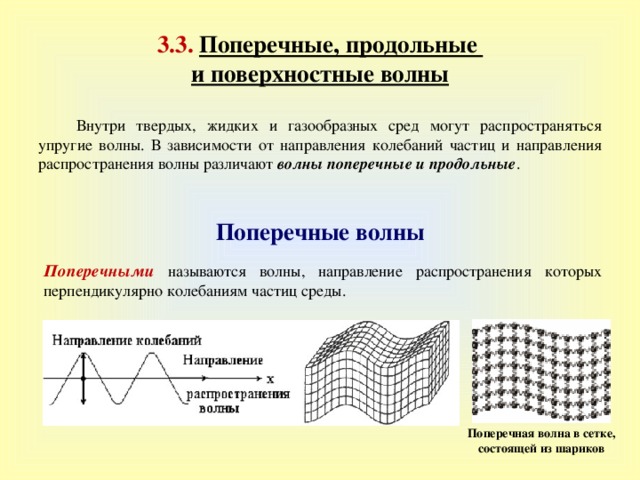
Поперечные волны
Поперечными называются волны, направление распространения которых перпендикулярно колебаниям частиц среды.
Поперечная волна в сетке, состоящей из шариков

Итак, как образуется волна?
Возьмем длинный резиновый шнур, один конец которого закрепим, а другим быстрым движением руки совершим однократное колебание в вертикальной плоскости.
Рука тянет конец шнура вверх, а поскольку концевой участок шнура « связан » с соседними участками, то им так же передается сила, действующая вверх, и они тоже начнут двигаться вверх. Один за другим последовательные участки шнура поднимаются вверх, и вдоль шнура движется гребень волны. Тем временем рука, держащая конец шнура, опускается в исходное положение – вниз, и участки шнура, уже пришедшие в верхнюю точку движения, в той же последовательности возвращаются в исходное состояние.
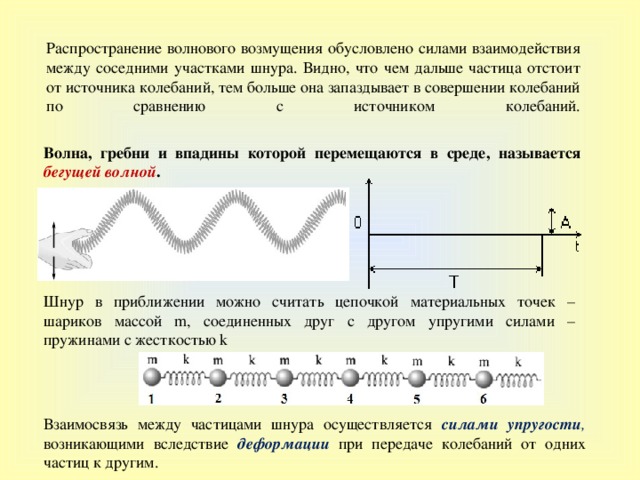
Распространение волнового возмущения обусловлено силами взаимодействия между соседними участками шнура. В идно, что чем дальше частица отстоит от источника колебаний, тем больше она запаздывает в совершении колебаний по сравнению с источником колебаний.
Волна, гребни и впадины которой перемещаются в среде, называется бегущей волной .
Шнур в приближении можно считать цепочкой материальных точек – шариков массой m , соединенных друг с другом упругими силами – пружинами с жесткостью k
Взаимосвязь между частицами шнура осуществляется силами упругости , возникающими вследствие деформации при передаче колебаний от одних частиц к другим.

Продольные волны
Не всякие волны можно увидеть. После удара молотком по ветви камертона мы слышим звук, хотя никаких волн в воздухе не видим.
Ударим по ветви камертона и поднесем к нему маленький шарик, звук будет слышно до тех пор, пока шарик будет отскакивать от камертона (это указывает на его колебания).
Ощущение звука в наших органах слуха возникает при периодическом изменении давления воздуха.
Колебания ветви камертона сопровождаются периодическими сжатиями и разрежениями воздуха вблизи нее.
Эти процессы сжатия и разрежения распространяются в воздухе во все стороны. Они и являются звуковыми волнами .
Камертон был изобретен в 1711 г . английским музыкантом Дж. Шором для настройки музыкальных инструментов

Звуковые волны являются примером продольных движений . При распространении звуковой волны частицы среды совершают колебания вдоль направления распространения волны.
Продольная волна в сетке, состоящей из шариков, скреплённых пружинками
Источник : http://physics.nad.ru/Physics/Cyrillic/wav_ref.htm
Волны, в которых колебания происходят вдоль направления распространения волны, называют продольными волнами .
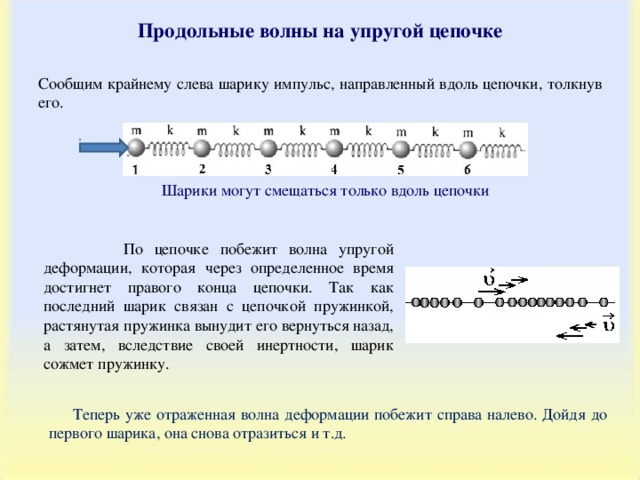
Продольные волны на упругой цепочке
Сообщим крайнему слева шарику импульс, направленный вдоль цепочки, толкнув его.
Шарики могут смещаться только вдоль цепочки
По цепочке побежит волна упругой деформации, которая через определенное время достигнет правого конца цепочки. Так как последний шарик связан с цепочкой пружинкой, растянутая пружинка вынудит его вернуться назад, а затем, вследствие своей инертности, шарик сожмет пружинку.
Теперь уже отраженная волна деформации побежит справа налево. Дойдя до первого шарика, она снова отразиться и т.д.
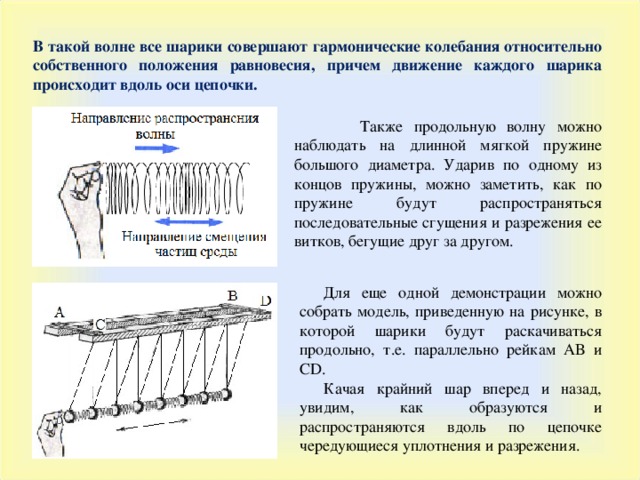
В такой волне все шарики совершают гармонические колебания относительно собственного положения равновесия, причем движение каждого шарика происходит вдоль оси цепочки.
Также продольную волну можно наблюдать на длинной мягкой пружине большого диаметра. Ударив по одному из концов пружины, можно заметить, как по пружине будут распространяться последовательные сгущения и разрежения ее витков, бегущие друг за другом.
Для еще одной демонстрации можно собрать модель, приведенную на рисунке, в которой шарики будут раскачиваться продольно, т.е. параллельно рейкам АВ и CD.
Качая крайний шар вперед и назад, увидим, как образуются и распространяются вдоль по цепочке чередующиеся уплотнения и разрежения.
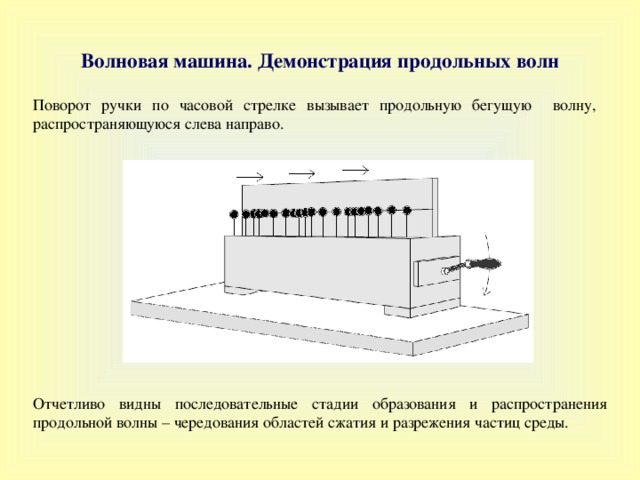
Волновая машина. Демонстрация продольных волн
Поворот ручки по часовой стрелке вызывает продольную бегущую волну, распространяющуюся слева направо.
О тчетливо видны последовательные стадии образования и распространения продольной волны – чередования областей сжатия и разрежения частиц среды.
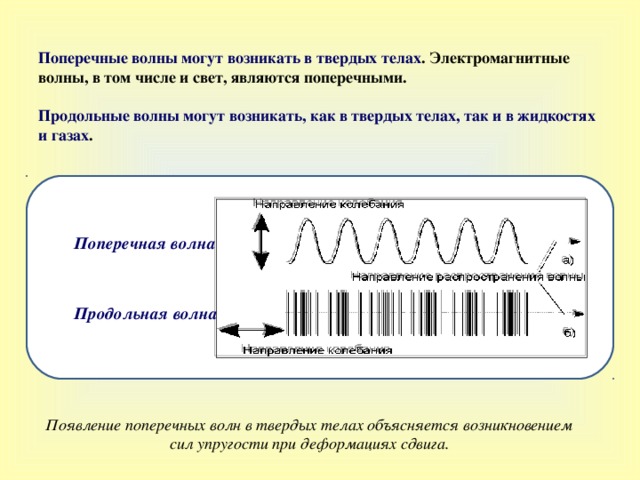
Поперечные волны могут возникать в твердых телах . Электромагнитные волны, в том числе и свет, являются поперечными. Продольные волны могут возникать, как в твердых телах, так и в жидкостях и газах .
Поперечная волна
Продольная волна
Появление поперечных волн в твердых телах объясняется возникновением сил упругости при деформациях сдвига.

Следует отличать скорость колебания отдельной частицы (колебательная скорость) от скорости распространения волны .
Скорость колебания отдельной частицы в процессе ее колебания меняется – когда частица проходит положение равновесия ее скорость максимальна, когда она отклонилась на расстояние, равное амплитуде, ее скорость становится равной нулю.
Появление поперечных волн в твердых телах объясняется возникновением сил упругости при деформациях сдвига.
Электромагнитные волны, в том числе и свет, являются поперечными.
Продольные волны могут возникать, как в твердых телах, так и в жидкостях и газах.

Поверхностные волны
Существуют еще волны и третьего типа – поверхностные волны – волны, распространяющиеся на границе раздела двух сред.
Волны на поверхности воды – один из примеров поверхностных волн, существующих на границе между водой и воздухом. Такие волны являются более сложными, т.к. имеют как поперечную, так и продольную компоненты.
Волны на поверхности воды
Волна на поверхности жидкости не является ни продольной, ни поперечной.
Красный шарик, моделирующий молекулу на поверхности жидкости, совершает круговое движение.
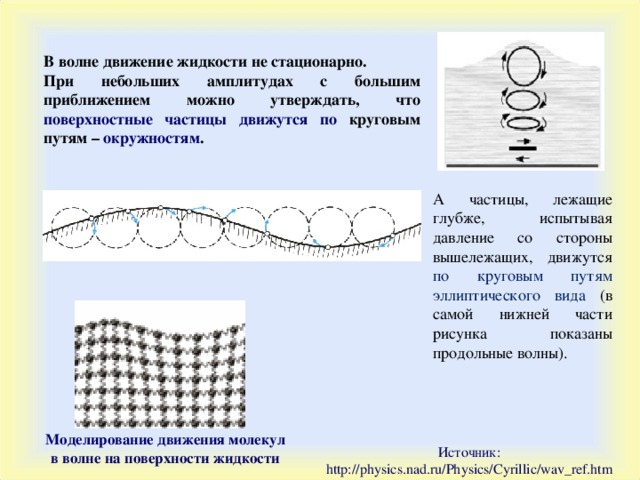
В волне движение жидкости не стационарно.
При небольших амплитудах с большим приближением можно утверждать, что поверхностные частицы движутся по круговым путям – окружностям .
А частицы, лежащие глубже, испытывая давление со стороны вышележащих, движутся по круговым путям эллиптического вида (в самой нижней части рисунка показаны продольные волны).
Моделирование движения молекул
в волне на поверхности жидкости
Источник : http://physics.nad.ru/Physics/Cyrillic/wav_ref.htm
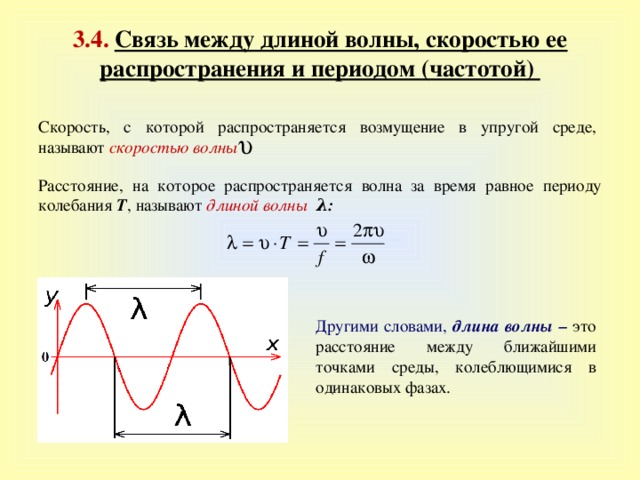
3.4 . Связь между длиной волны, скоростью ее распространения и периодом (частотой)
Скорость, с которой распространяется возмущение в упругой среде, называют скоростью волны
Расстояние, на которое распространяется волна за время равное периоду колебания Т , называют длиной волны λ :
Другими словами, длина волны – это расстояние между ближайшими точками среды, колеблющимися в одинаковых фазах .

3 . 5. Волновая поверхность и фронт волны
Волновая поверхность – это поверхность, проведенная через равновесные положения частиц среды, совершающих колебания в одинаковой фазе.
Другими словами, волновая поверхность – это геометрическое место точек, колеблющихся в одинаковой фазе.
для плоской гармонической волны
В Ы В О Д Ы :
- Число волновых поверхностей – бесконечно .
- Волновые поверхности неподвижны .
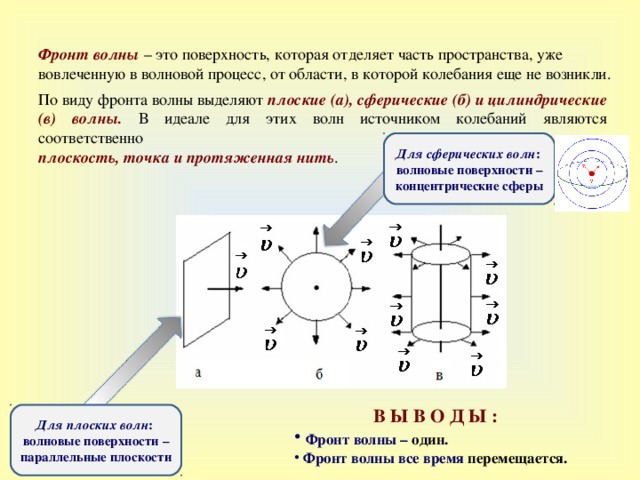
Фронт волны – это поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли.
По виду фронта волны выделяют плоские (а), сферические (б) и цилиндрические (в) волны . В идеале для этих волн источником колебаний являются соответственно
плоскость, точка и протяженная нить .
Для сферических волн : волновые поверхности – концентрические сферы
В Ы В О Д Ы :
- Фронт волны – один .
- Фронт волны все время перемещается.
Для плоских волн : волновые поверхности – параллельные плоскости
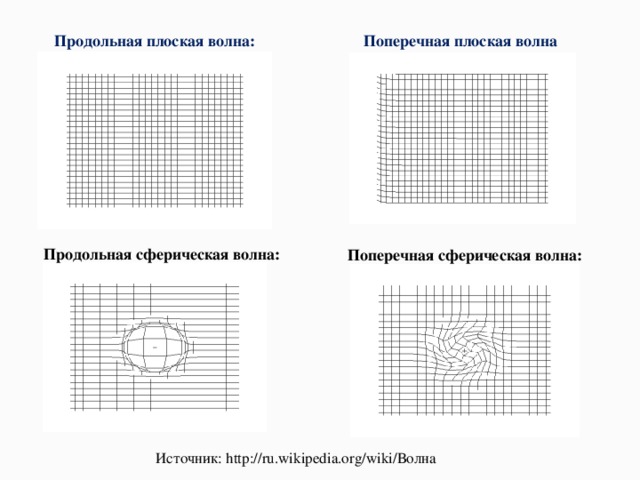
Продольная плоская волна:
Поперечная плоская волна
Продольная сферическая волна:
Поперечная сферическая волна:
Источник : http://ru.wikipedia.org/wiki/ Волна

В случае, если сферический или цилиндрический источник/источники волны в процессе излучения движется по некоторой замкнутой кривой, то образуется спиральная волна
Источник : http://selftrans.narod.ru/v4_1/quant/quant67/agfig26.gif

3 . 6. Уравнение плоской волны (смещение частиц среды в бегущей волне)
Плоская волна распространяется только в одном направлении и представляет собой идеализацию, которая лишь приблизительно реализуется на практике.
В плоской волне волновые поверхности будут представлять совокупность плоскостей, параллельных друг другу.
Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат и времени.
Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно, периодически повторяющееся движение).
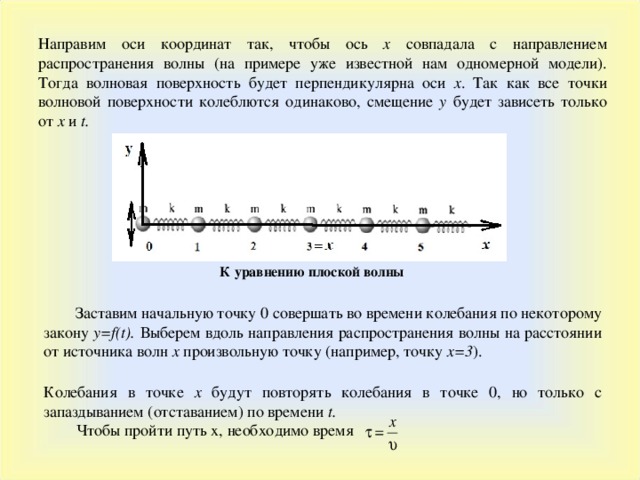
Направим оси координат так, чтобы ось x совпадала с направлением распространения волны (на примере уже известной нам одномерной модели). Тогда волновая поверхность будет перпендикулярна оси x . Так как все точки волновой поверхности колеблются одинаково, смещение y будет зависеть только от х и t.
К уравнению плоской волны
Заставим начальную точку 0 совершать во времени колебания по некоторому закону y = f ( t ). Выберем вдоль направления распространения волны на расстоянии от источника волн x произвольную точку (например, точку x =3 ).
Колебания в точке х будут повторять колебания в точке 0, но только с запаздыванием (отставанием) по времени t.
Чтобы пройти путь x, необходимо время

Тогда в общем виде уравнение незатухающей волны, которая распространяется вдоль положительного направления оси х со скоростью υ можно записать как :
Если же колебания частиц происходят по гармоническому закону, то
Значит
причем
называется волновым числом.
Таким образом, уравнение плоской волны , которая распространяется вдоль положительного направления оси х со скоростью υ в среде, не поглощающей энергию (т.е. амплитуда колебаний неизменна :
где х – расстояние от источника волн до рассматриваемой точки среды вдоль направления распространения волны, y(x,t) – координата гармонического колебания данной точки, φ 0 – начальная фаза гармонического колебания источника волн, Xm – амплитуда волны , ω – циклическая частота.
![3 . 7. Поток энергии и интенсивность волны. Вектор Умова Количественной характеристикой перенесенной энергии является поток энергии. Представление о потоке энергии, переносимой волнами, впервые дал в 1874 г. ученый-физик Николай Алексеевич Умов. Поток энергии волн (Ф) равен отношению энергии, переносимой волнами через некоторую поверхность, ко времени, в течение которого эта энергия перенесена Интенсивность (или плотность потока энергии) волны ( I ) – отношение потока энергии Ф к площади S поверхности, расположенной перпендикулярно направлению распространения волны: [ Вт/м 2 ]](https://fsd.videouroki.net/html/2013/10/19/98666711/img29.jpg)
3 . 7. Поток энергии и интенсивность волны. Вектор Умова
Количественной характеристикой перенесенной энергии является поток энергии. Представление о потоке энергии, переносимой волнами, впервые дал в 1874 г. ученый-физик Николай Алексеевич Умов.
Поток энергии волн (Ф) равен отношению энергии, переносимой волнами через некоторую поверхность, ко времени, в течение которого эта энергия перенесена
Интенсивность (или плотность потока энергии) волны ( I ) – отношение потока энергии Ф к площади S поверхности, расположенной перпендикулярно направлению распространения волны:
[ Вт/м 2 ]

Итак, интенсивност ь ( I ) – величина, определяемая средней по времени энергией , переносимой волной в единицу времени сквозь единичную площадку, перпендикулярную направлению распространения волны.
3 . 8. Понятие о линейных и нелинейных волнах
Волна называется линейной , если свойства среды для этой волны не зависят от интенсивности волны . Линейные волны не влияют на прохождение других волн и распространяются независимо друг от друга без каких-либо искажений.
Нелинейная волна – это волна, под действием которой меняются свойства среды и соответственно меняются свойства самой волны , что обычно происходит при большой интенсивности волны.

Источники
- Воронкин А.С. Линейные колебания и волны: Введение в акустику : уч. пособ. А. С. Воронкин. – Луганськ : СПД Рєзніков В.С., 2012. – 224 с.
- Асламазов Л. Что такое волна? / Л. Асламазов, И. Кикоин // Научно-популярный физико-математический журнал «Квант», 1982. – №6. – С. 2–7.
- Асламазов Л. Уравнение волны / Л. Асламазов // Научно-популярный физико-математический журнал «Квант», 1984. – №11. – С. 27–28.
- Асламазов Л. Как волны передают информацию? / Л. Асламазов // Научно-популярный физико-математический журнал «Квант», 1986. – №8. – С. 20–24.
- Воронкин А. С. Введение в физику звука / А. С. Воронкин. – Луганск : Изд-во ЛГИКИ, 2012. – 96 с.
- Кузнецов Е. О волнах на море и ряби на лужах / Е. Кузнецов, А. Рубенчик // Научно-популярный физико-математический журнал «Квант», 1980. – №9. – С. 22–26.
- Островский Л. Волны на воде / Л. Островский // Научно-популярный физико-математический журнал «Квант», 1987. – № 8. – С. 16–22.
![7. Перкальскис Б. Ш. Волновые явления и демонстрации по курсу физики / Б. Ш. Перкальскис. – Томск : Изд-во Томск. ун-та, 1984. – 280 с. 8. Руденко О., Черкезян В. В мире мощного звука / О. Руденко, В. Черкезян // Научно-популярный физико-математический журнал «Квант», 1989. – №9. – С. 19–25. Рыдник В. И. О современной акустике : книга для внеклассного чтения / В. И. Рыдник. – М. : Просвещение, 1979. – 80 с. Стонг К. Исследование волн на поверхности воды / К. Стонг // Научно-популярный физико-математический журнал «Квант», 1972. – № 5. –С. 20–24. Чедд Г. Звук / Грэхэм Чедд ; [пер. с англ. Г. Кузнецова]. – М. : Мир, 1975. – 206 с. Элементарный учебник физики : учебное пособие в 3-х т. / Под ред. Г. С. Ландсберга. – Т. III . Колебания и волны. Оптика. Атомная и ядерная физика. – М. : Наука, 1986. – 656 с. Интернет-ресурсы](https://fsd.videouroki.net/html/2013/10/19/98666711/img32.jpg)
7. Перкальскис Б. Ш. Волновые явления и демонстрации по курсу физики / Б. Ш. Перкальскис. – Томск : Изд-во Томск. ун-та, 1984. – 280 с.
8. Руденко О., Черкезян В. В мире мощного звука / О. Руденко, В. Черкезян // Научно-популярный физико-математический журнал «Квант», 1989. – №9. – С. 19–25.
- Рыдник В. И. О современной акустике : книга для внеклассного чтения / В. И. Рыдник. – М. : Просвещение, 1979. – 80 с.
- Стонг К. Исследование волн на поверхности воды / К. Стонг // Научно-популярный физико-математический журнал «Квант», 1972. – № 5. –С. 20–24.
- Чедд Г. Звук / Грэхэм Чедд ; [пер. с англ. Г. Кузнецова]. – М. : Мир, 1975. – 206 с.
- Элементарный учебник физики : учебное пособие в 3-х т. / Под ред. Г. С. Ландсберга. – Т. III . Колебания и волны. Оптика. Атомная и ядерная физика. – М. : Наука, 1986. – 656 с.
- Интернет-ресурсы


 Получите свидетельство
Получите свидетельство Вход
Вход































![3 . 7. Поток энергии и интенсивность волны. Вектор Умова Количественной характеристикой перенесенной энергии является поток энергии. Представление о потоке энергии, переносимой волнами, впервые дал в 1874 г. ученый-физик Николай Алексеевич Умов. Поток энергии волн (Ф) равен отношению энергии, переносимой волнами через некоторую поверхность, ко времени, в течение которого эта энергия перенесена Интенсивность (или плотность потока энергии) волны ( I ) – отношение потока энергии Ф к площади S поверхности, расположенной перпендикулярно направлению распространения волны: [ Вт/м 2 ]](https://fsd.videouroki.net/html/2013/10/19/98666711/img29.jpg)


![7. Перкальскис Б. Ш. Волновые явления и демонстрации по курсу физики / Б. Ш. Перкальскис. – Томск : Изд-во Томск. ун-та, 1984. – 280 с. 8. Руденко О., Черкезян В. В мире мощного звука / О. Руденко, В. Черкезян // Научно-популярный физико-математический журнал «Квант», 1989. – №9. – С. 19–25. Рыдник В. И. О современной акустике : книга для внеклассного чтения / В. И. Рыдник. – М. : Просвещение, 1979. – 80 с. Стонг К. Исследование волн на поверхности воды / К. Стонг // Научно-популярный физико-математический журнал «Квант», 1972. – № 5. –С. 20–24. Чедд Г. Звук / Грэхэм Чедд ; [пер. с англ. Г. Кузнецова]. – М. : Мир, 1975. – 206 с. Элементарный учебник физики : учебное пособие в 3-х т. / Под ред. Г. С. Ландсберга. – Т. III . Колебания и волны. Оптика. Атомная и ядерная физика. – М. : Наука, 1986. – 656 с. Интернет-ресурсы](https://fsd.videouroki.net/html/2013/10/19/98666711/img32.jpg)









 Волновые процессы (4.3 MB)
Волновые процессы (4.3 MB)
 0
0 4243
4243 136
136 Нравится
0
Нравится
0


