Внеклассное мероприятие по математике "Золотое сечение"

«Золотое сечение»

Формирование навыков исследовательской деятельности учащихся через познание законов красоты и гармонии окружающего мира.

С тех пор как существует мирозданье, Такого нет, что б не нуждался в знанье, Какой мы не возьмем, язык и век, Всегда стремится к знанью человек.

«…Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем…»

Иоганн Кеплер

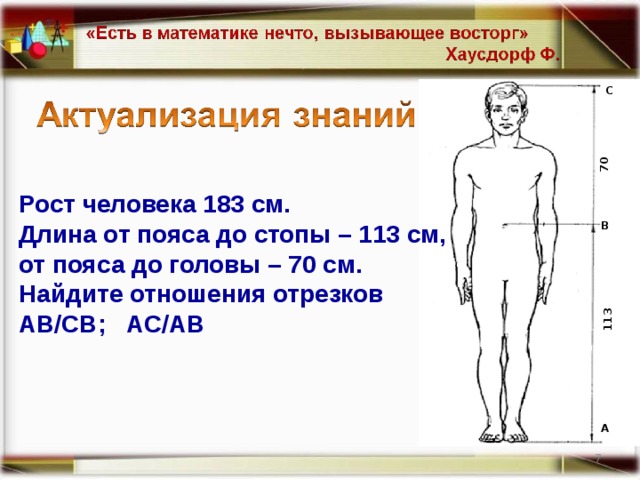
113

70

С

Рост человека 183 см.

Длина от пояса до стопы – 113 см,

от пояса до головы – 70 см.

Найдите отношения отрезков АВ/СВ; АС/АВ

В

А

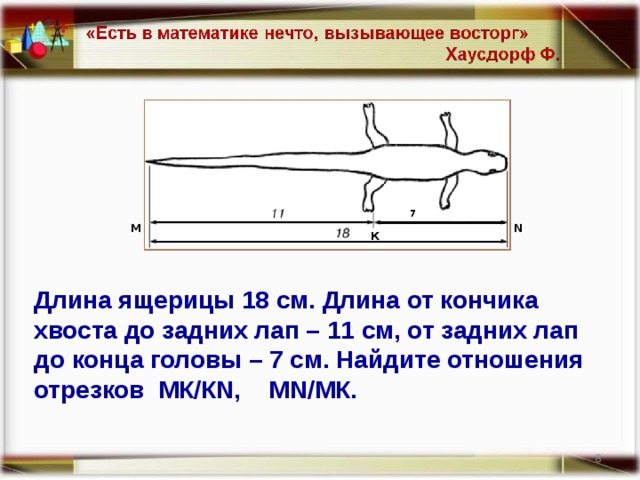
М

N

К

Длина ящерицы 18 см. Длина от кончика хвоста до задних лап – 11 см, от задних лап до конца головы – 7 см. Найдите отношения отрезков МК/К N , М N /МК.

7

Почему отношения некоторых чисел или величин равны одному и тому же числу, приблизительно 0,6. Есть ли в этом какая-то закономерность?

8

«Можно ли проверить алгеброй гармонию?».

А.С. Пушкин

8

Определение «золотого сечения»: целое относится к его большей части так же, как большая часть относится к меньшей части.

План построения:

1.Постройте прямой угол В.

2.На одной стороне угла от вершины В отложите катет В D

3.На второй стороне угла от вершины В отложите катет ВА равный 2 BD . Проведите гипотенузу А D .

3.Проведите окружность с центром в точке D и радиусом В D . На гипотенузе отметьте точку Е

4.Проведите окружность с центром в точке А и радиусом АЕ. На катете АВ отметьте точку С

5. С - точка золотого сечения.

АС:АВ=СВ:АС

С

А

В

x

1 -x

1

Пусть весь отрезок АВ = 1. Составьте пропорцию и решите уравнение.

D

E

C

B

A

8

Число φ 1,6180339887….

в 13 веке открыл итальянский математик Фибоначчи. Но "Золотое сечение" знали ещё древние.

Золотым называется такой равнобедренный треугольник , основание и боковая сторона которого находятся в золотом отношении:

А

В

С

Прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение длины к ширине даёт число φ , называется золотым прямоугольником.

14

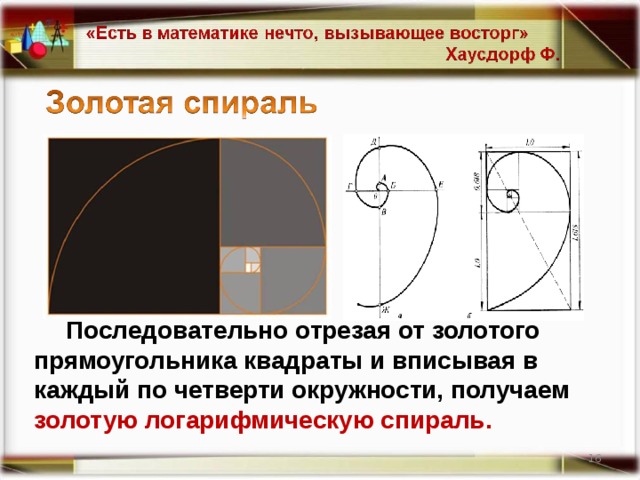
Последовательно отрезая от золотого прямоугольника квадраты и вписывая в каждый по четверти окружности, получаем золотую логарифмическую спираль.

14

Если в пентаграмме провести все диагонали, то в результате получим пятиугольную звезду .

Точки пересечения диагоналей в пентаграмме являются точками золотого сечения диагоналей (отношение синего отрезка к зелёному, красного к синему, зелёного к фиолетовому, равны 1.618). При этом эти точки образуют новую пентаграмму

Здание военного ведомства США имеет форму пентаграммы и получило название «Пентагон», что значит правильный пятиугольник.

14

19.04.18

http://aida.ucoz.ru

14

14

14

14

14

Эпоха Возрождения ассоциируется с именем Леонардо да Винчи.

Имеется много авторитетных свидетельств о том, что именно Леонардо да Винчи(1452-1519) был одним из первых, кто ввел сам термин «Золотое Сечение».

Доказано, что во многих своих произведениях Леонардо да Винчи использовал пропорции золотого сечения, в частности, в своей всемирно известной фреске «Тайная вечеря» и непревзойденной «Джоконде».

14

Сандро Ботичелли «Рождение Венеры» (около 1485 г).

Пропорции Венеры выполнены в золотом сечении.

14

«Аппассионата» – одно из самых совершенных по форме произведений в мировой музыке.

В первой части «Аппассионаты», где интенсивно развиваются темы и сменяют друг друга тональности, - два основных раздела. В первом 43,25 такта, во втором – 26,75. Отношение 43,25:26,75=0,618:0,382=1,618 дает золотое сечение.

14

А.С. Пушкина

"Сапожник":

Картину раз высматривал сапожник И в обуви ошибку указал; Взяв тотчас кисть, исправился художник, Вот, подбочась, сапожник продолжал: "Мне кажется, лицо немного криво ... А эта грудь не слишком ли нага? Тут Апеллес прервал нетерпеливо: "Суди, дружок, не выше сапога!" Есть у меня приятель на примете: Не ведаю, в каком бы он предмете Был знатоком, хоть строг он на словах, Но черт его несет судить о свете: Попробуй он судить о сапогах!

Проведем анализ этой притчи. Стихотворение состоит из 13 строк. В нем выделяется две смысловые части: первая в 8 строк и вторая (мораль притчи) в 5 строк (13, 8, 5 - числа Фибоначчи).

14

14

14

14

14

1. http://images.yandex.ru/ http://ru.wikipedia.org/wiki

2. http://n-t.ru/tp/iz/zs.htm

3. http://arx.novosibdom.ru/node/419

4. http://festival.1september.ru/articles/532746/

5. http://nsportal.ru/shkola/algebra/library/zolotoe-sechenie-v-matematike

6. http://www.zaitseva-irina.ru/html/f1103454898.html

7. http://tagrigoreva1.narod.ru/internet_urok.htm

14