Внеклассное мероприятие по математике: «Кто хочет стать отличником»
Цели и задачи урока:
1. вспомнить основные математические понятия и термины.
2. формировать благоприятную атмосферу для дальнейшего изучения дисциплин математического цикла.
Продолжить обучать умению: самостоятельно мыслить; осваивать информацию и логически ее перерабатывать; вырабатывать собственную позицию, обосновывать ее и защищать
1 Отборочный тур:
Сопоставить математические действия и обратные к ним:
1) деление; 2) возведение в степень; 3) вычитание; 4) извлечение корня:
а) умножение; б) извлечение корня; в) возведение в степень; г)сложение.
1 игра
1. Приведенное квадратное уравнение можно решить при помощи:
а) Т. Пифагора; б) Т. Фалеса; в) Т. Виета; г) признаков делимости.
2. Какой из этих формул нет среди формул сокращенного умножения?
а) квадрат суммы; б) разность кубов; в) куб разности; г) сумма квадратов.
3. Центр описанной около треугольника окружности — точка пересечения:
а) биссектрис; б) серединных перпендикуляров; в) медиан; г) высот.
4. Комбинация математических знаков и букв, выражающая какое-либо
предложение называется:
а) функция; б) тождество; в) равенство; г) формула.
5. Что позволяет отыскать среди данных чисел простые?
а) треугольник Паскаля; б) решето Эратосфена; в) кубик Рубика; г)бином Ньютона.
6. Число, которое равняется сумме всех своих делителей (исключая само это число) называется:
а) совершенным; б) идеальным; в) простым; г) великолепным.
7. В каком треугольнике высоты пересекаются в одной из его вершин?
а) тупоугольном; б) равнобедренном;
в) равностороннем; г) прямоугольном.
8. Математик, которого называют отцом алгебры - это:
а) Франсуа Виет; б) Джероламо Кордано;
в) Муса — аль-Хорезми; г) Эварист Галуа.
9. Иррациональное число - это:
а) конечная десятичная дробь; б) бесконечная непериодическая десятичная дробь;
в) бесконечная периодическая десятичная дробь.
10. Половина - треть его. О каком числе идет речь?
а) 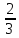 б) 1,5; в) нет такого числа; г)
б) 1,5; в) нет такого числа; г) 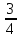
2 Отборочный тур:
Расположите в порядке изучения неравенств в школе:
а) линейное; б) дробное; в) квадратное; г) числовые.
2 игра
1. Арбуз на 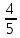 кг тяжелее, чем
кг тяжелее, чем 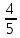 арбуза. Сколько весит арбуз?
арбуза. Сколько весит арбуз?
а) 5 кг; б) 4 кг; в) 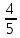 кг; г)
кг; г) 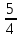 кг
кг
2. Товар сначала подешевел на 10%, затем подорожал на 10%. В результате цена товара:
а) осталась прежней; б) повысилась;
в) понизилась; г) невозможно определить.
3. Смешали 2 л сока с 10% содержанием сахара и 3 л с 15% содержанием сахара, тогда % содержания сахара в смеси:
а) 5%; 6)25%; в) 12,5%; г) 13%.
4. Кирпич весит полкирпича и еще 1,5 кг. Сколько весит кирпич?
а) 2кг; б) 3 кг; в) 0,75 кг; г) 0,5 кг..
5. У Пети на куртке 3 кармана. Сколькими способами он монет положить в эти карманы 2 одинаковые монеты?
а) 6; 6)3; в) 4; г) 2.
6. Числа-близнецы - это:
а) противоположные числа; б) простые числа, разность которых равна 2;
в) равные десятичные и обыкновенные дроби; г) таких чисел нет.
7. Как называются треугольники со сторонами 13, 14, 15 или 51, 52, 53?
а) египетскими; б) диофантовыми;
в) не имеют определенного названия; г) героновыми.
8. Центр тяжести треугольника - это точка пересечения :
а) медиан; б) высот; в) биссектрис; г) серединных перпендикуляров.
9. Пруд зарастает кувшинками. Площадь, занимаемая ими, ежедневно удваивается.
За 29 дней пруд зарос наполовину. За какое время пруд зарастет полностью?
а) 58; 6)30; в) 33; г)87.
10. Метод координат возник благодаря работам:
а) Э. Безу; б) Ф. Виета; в) Р. Декарта; г) Л. Эйлера.
3 Отборочный тур:
Расположите геометрические объекты по количеству вершин, начиная с наибольшего:
а) треугольник; б) куб; в) угол; г) ромб.
3 игра
1. Какое из этих словосочетаний не является правильным математическим термином?
а) среднее геометрическое; б) среднее гармоническое;
в) среднее логическое; г) среднее арифметическое.
2. На черно-белой фотографии черный цвет составляет 80% площади. Эту фотографию увеличили в 3 раза. Какой процент составляет белый цвет на увеличенной фотографии?
а) 20%; 6)30%; в) 40%; г) 80%.
3. Площадь правильного треугольника равна 3 6. Отрежем от каждой вершины по маленькому правильному треугольнику так, чтобы остался правильный шестиугольник. Какова площадь этого шестиугольника?
а) 26; 6) 24; в) 28; г) 30.
4. Первая русская женщина математик Софья Ковалевская стала систематически изучать курс высшей математики с:
а) 10 лет; б) 15 лет; в) 5 лет; г) 18 лет
5. Кому принадлежит создание первой счетной машины?
а) Леонарду Эйлеру; б) Бонавентура Кавальери;
в) Карлу Фридриху Гауссу; г) Блезу Паскалю.
6. Тригонометрические формулы, позволяющие определить sin и cos углов, больших 90° называются формулами:
а) сложения; 6) приведения; в) уменьшения; г) изменения.
7. Равенство, верное при любых значениях входящих в него букв называется:
а) уравнение; б) выражение; в) неравенство; г) тождество.
8. Какое равенство не может быть верным?
а)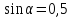 ; 6)
; 6) 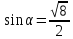 в)
в) 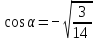 г)
г) 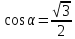
9. Какое утверждение не является верным? В 1 точке пересекаются
а) высоты треугольника; б) средние линии треугольника;
в) медианы треугольника; г) биссектрисы треугольника.
10. Велосипедист ехал 2 ч со скоростью 10 км/ч и 1ч со скоростью 7 км/ч. Какова его средняя скорость?
а) 8,5 км/ч; б) 27 км/ч; в) 5,66 км/ч; г) 9 км/ч.
4 Отборочный тур:
Расположите в порядке убывания:
а)-2; 6)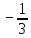 ; в)
; в) 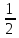 ; г) 0,6.
; г) 0,6.
4 игра
1. Семь осликов за 3 дня съедают 21 мешок корма. Сколько корма нужно 5 осликам на 5 дней?
а) 25; 6)20; в) 15; г) 10.
2. Выберите «лишний» термин среди следующих:
а) отрезок; б) интервал; в) модуль; г) луч.
3. Алгебраическое уравнение n-степени:
а) всегда имеет n корней; б) имеет не более n корней;
в) имеет не менее n корней; г) не имеет корней.
4. Ортоцентр треугольника - это точка пересечения:
а) медиан; б) высот; в) биссектрис; г) серединных перпендикуляров.
5. Вадим участвует в соревнованиях по бегу. В какой- то момент оказалось, что впереди него бежит треть всех участников, сзади — половина, а рядом с ним никого нет. Сколько человек участвуют в забеге?
а) 5; 6)12; в) 6; г)18.
6. Раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций можно составить из заданных объектов - это:
а) арифметика; б) тригонометрия; в) комбинаторика; г) геометрия.
7. Какое из этих чисел не равно остальным?
а)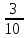 ; б)
; б)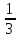 ; в) 30% от 1; г) 0,3.
; в) 30% от 1; г) 0,3.
8. Сколько осей симметрии имеет квадрат?
а) 4; 6)6; в) 8; г) 2.
9. Баранка имеет форму:
а) эллипсоида б) тора; в) цилиндра; г)многогранника.
10. Лобачевский Николай Иванович в 1826 г. сделал сообщение об открытии новой
а) формулы; б) теоремы; в) геометрии; г) гипотезы.
КАРТОЧКИ
1игра
| 1.Приведенное квадратное уравнение можно решить при помощи: а) Т. Пифагора; б) Т. Фалеса; в) Т. Виета; г) признаков делимости.
| 1.Приведенное квадратное уравнение можно решить при помощи: а) Т. Пифагора; б) Т. Фалеса; в) Т. Виета; г) признаков делимости.
|
| 2. Какой из этих формул нет среди формул сокращенного умножения? а) квадрат суммы; б) разность кубов; в) куб разности; г) сумма квадратов.
| 2. Какой из этих формул нет среди формул сокращенного умножения? а) квадрат суммы; б) разность кубов; в) куб разности; г) сумма квадратов.
|
| 3. Центр описанной около треугольника окружности — точка пересечения: а) биссектрис; б) серединных перпендикуляров; в) медиан; г) высот.
| 3. Центр описанной около треугольника окружности — точка пересечения: а) биссектрис; б) серединных перпендикуляров; в) медиан; г) высот.
|
| 4. Комбинация математических знаков и букв, выражающая какое-либо предложение называется: а) функция; б) тождество; в) равенство; г) формула.
| 4. Комбинация математических знаков и букв, выражающая какое-либо предложение называется: а) функция; б) тождество; в) равенство; г) формула.
|
| 5. Что позволяет отыскать среди данных чисел простые? а) треугольник Паскаля; б) решето Эратосфена; в) кубик Рубика; г)бином Ньютона.
| 5. Что позволяет отыскать среди данных чисел простые? а) треугольник Паскаля; б) решето Эратосфена; в) кубик Рубика; г)бином Ньютона.
|
| 6. Число, которое равняется сумме всех своих делителей (исключая само это число) называется: а) совершенным; б) идеальным; в) простым; г) великолепным.
| 6. Число, которое равняется сумме всех своих делителей (исключая само это число) называется: а) совершенным; б) идеальным; в) простым; г) великолепным.
|
| 7. В каком треугольнике высоты пересекаются в одной из его вершин? а) тупоугольном; б) равнобедренном; в) равностороннем; г) прямоугольном.
| 7. В каком треугольнике высоты пересекаются в одной из его вершин? а) тупоугольном; б) равнобедренном; в) равностороннем; г) прямоугольном.
|
| 8. Математик, которого называют отцом алгебры - это: а) Франсуа Виет; б) Джероламо Кордано; в) Муса — аль-Хорезми; г) Эварист Галуа.
| 8. Математик, которого называют отцом алгебры - это: а) Франсуа Виет; б) Джероламо Кордано; в) Муса — аль-Хорезми; г) Эварист Галуа.
|
| 9. Иррациональное число - это: а) конечная десятичная дробь; б) бесконечная непериодическая десятичная дробь; в) бесконечная периодическая десятичная дробь.
| 9. Иррациональное число - это: а) конечная десятичная дробь; б) бесконечная непериодическая десятичная дробь; в) бесконечная периодическая десятичная дробь.
|
| 10. Половина - треть его. О каком числе идет речь? а) в) нет такого числа; г)
| 10. Половина - треть его. О каком числе идет речь? а) в) нет такого числа; г)
|
2 игра
| 1. Арбуз на а) 5 кг; б) 4 кг; в)
| 1. Арбуз на а) 5 кг; б) 4 кг; в)
|
| 2. Товар сначала подешевел на 10%, затем подорожал на 10%. В результате цена товара: а) осталась прежней; б) повысилась; в) понизилась; г) невозможно определить.
| 2. Товар сначала подешевел на 10%, затем подорожал на 10%. В результате цена товара: а) осталась прежней; б) повысилась; в) понизилась; г) невозможно определить.
|
| 3. Смешали 2 л сока с 10% содержанием сахара и 3 л с 15% содержанием сахара, тогда % содержания сахара в смеси: а) 5%; 6)25%; в) 12,5%; г) 13%.
| 3. Смешали 2 л сока с 10% содержанием сахара и 3 л с 15% содержанием сахара, тогда % содержания сахара в смеси: а) 5%; 6)25%; в) 12,5%; г) 13%.
|
| 4. Кирпич весит полкирпича и еще 1,5 кг. Сколько весит кирпич? а) 2кг; б) 3 кг; в) 0,75 кг; г) 0,5 кг..
| 4. Кирпич весит полкирпича и еще 1,5 кг. Сколько весит кирпич? а) 2кг; б) 3 кг; в) 0,75 кг; г) 0,5 кг..
|
| 5. У Пети на куртке 3 кармана. Сколькими способами он монет положить в эти карманы 2 одинаковые монеты? а) 6; 6)3; в) 4; г) 2.
| 5. У Пети на куртке 3 кармана. Сколькими способами он монет положить в эти карманы 2 одинаковые монеты? а) 6; 6)3; в) 4; г) 2.
|
| 6. Числа-близнецы - это: а) противоположные числа; б) простые числа, разность которых равна 2; в) равные десятичные и обыкновенные дроби; г) таких чисел нет.
| 6. Числа-близнецы - это: а) противоположные числа; б) простые числа, разность которых равна 2; в) равные десятичные и обыкновенные дроби; г) таких чисел нет.
|
| 7. Как называются треугольники со сторонами 13, 14, 15 или 51, 52, 53? а) египетскими; б) диофантовыми; в) не имеют определенного названия; г) героновыми.
| 7. Как называются треугольники со сторонами 13, 14, 15 или 51, 52, 53? а) египетскими; б) диофантовыми; в) не имеют определенного названия; г) героновыми.
|
| 8. Центр тяжести треугольника - это точка пересечения : а) медиан; б) высот; в) биссектрис; г) серединных перпендикуляров.
| 8. Центр тяжести треугольника - это точка пересечения : а) медиан; б) высот; в) биссектрис; г) серединных перпендикуляров.
|
| 9. Пруд зарастает кувшинками. Площадь, занимаемая ими, ежедневно удваивается. За 29 дней пруд зарос наполовину. За какое время пруд зарастет полностью? а) 58; 6)30; в) 33; г)87.
| 9. Пруд зарастает кувшинками. Площадь, занимаемая ими, ежедневно удваивается. За 29 дней пруд зарос наполовину. За какое время пруд зарастет полностью? а) 58; 6)30; в) 33; г)87.
|
| 10. Метод координат возник благодаря работам: а) Э. Безу; б) Ф. Виета; в) Р. Декарта; г) Л. Эйлера.
| 10. Метод координат возник благодаря работам: а) Э. Безу; б) Ф. Виета; в) Р. Декарта; г) Л. Эйлера.
|
3 игра
| 1. Какое из этих словосочетаний не является правильным математическим термином? а) среднее геометрическое; б) среднее гармоническое; в) среднее логическое; г) среднее арифметическое.
| 1. Какое из этих словосочетаний не является правильным математическим термином? а) среднее геометрическое; б) среднее гармоническое; в) среднее логическое; г) среднее арифметическое.
|
| 2. На черно-белой фотографии черный цвет составляет 80% площади. Эту фотографию увеличили в 3 раза. Какой процент составляет белый цвет на увеличенной фотографии? а) 20%; 6)30%; в) 40%; г) 80%.
| 2. На черно-белой фотографии черный цвет составляет 80% площади. Эту фотографию увеличили в 3 раза. Какой процент составляет белый цвет на увеличенной фотографии? а) 20%; 6)30%; в) 40%; г) 80%.
|
| 3. Площадь правильного треугольника равна 3 6. Отрежем от каждой вершины по маленькому правильному треугольнику так, чтобы остался правильный шестиугольник. Какова площадь этого шестиугольника? а) 26; 6) 24; в) 28; г) 30.
| 3. Площадь правильного треугольника равна 3 6. Отрежем от каждой вершины по маленькому правильному треугольнику так, чтобы остался правильный шестиугольник. Какова площадь этого шестиугольника? а) 26; 6) 24; в) 28; г) 30.
|
| 4. Первая русская женщина математик Софья Ковалевская стала систематически изучать курс высшей математики с: а) 10 лет; б) 15 лет; в) 5 лет; г) 18 лет
| 4. Первая русская женщина математик Софья Ковалевская стала систематически изучать курс высшей математики с: а) 10 лет; б) 15 лет; в) 5 лет; г) 18 лет
|
| 5. Кому принадлежит создание первой счетной машины? а) Леонарду Эйлеру; б) Бонавентура Кавальери; в) Карлу Фридриху Гауссу; г) Блезу Паскалю.
| 5. Кому принадлежит создание первой счетной машины? а) Леонарду Эйлеру; б) Бонавентура Кавальери; в) Карлу Фридриху Гауссу; г) Блезу Паскалю.
|
| 6. Тригонометрические формулы, позволяющие определить sin и cos углов, больших 90° называются формулами: а) сложения; 6) приведения; в) уменьшения; г) изменения.
| 6. Тригонометрические формулы, позволяющие определить sin и cos углов, больших 90° называются формулами: а) сложения; 6) приведения; в) уменьшения; г) изменения.
|
| 7. Равенство, верное при любых значениях входящих в него букв называется: а) уравнение; б) выражение; в) неравенство; г) тождество.
| 7. Равенство, верное при любых значениях входящих в него букв называется: а) уравнение; б) выражение; в) неравенство; г) тождество.
|
| 8. Какое равенство не может быть верным? а) в)
| 8. Какое равенство не может быть верным? а) в)
|
| 9. Какое утверждение не является верным? В 1 точке пересекаются а) высоты треугольника; б) средние линии треугольника; в) медианы треугольника; г) биссектрисы треугольника.
| 9. Какое утверждение не является верным? В 1 точке пересекаются а) высоты треугольника; б) средние линии треугольника; в) медианы треугольника; г) биссектрисы треугольника.
|
| 10. Велосипедист ехал 2 ч со скоростью 10 км/ч и 1ч со скоростью 7 км/ч. Какова его средняя скорость? а) 8,5 км/ч; б) 27 км/ч; в) 5,66 км/ч; г) 9 км/ч.
| 10. Велосипедист ехал 2 ч со скоростью 10 км/ч и 1ч со скоростью 7 км/ч. Какова его средняя скорость? а) 8,5 км/ч; б) 27 км/ч; в) 5,66 км/ч; г) 9 км/ч.
|
4 игра
| 1. Семь осликов за 3 дня съедают 21 мешок корма. Сколько корма нужно 5 осликам на 5 дней? а) 25; 6)20; в) 15; г) 10.
| 1. Семь осликов за 3 дня съедают 21 мешок корма. Сколько корма нужно 5 осликам на 5 дней? а) 25; 6)20; в) 15; г) 10.
|
| 2. Выберите «лишний» термин среди следующих: а) отрезок; б) интервал; в) модуль; г) луч.
| 2. Выберите «лишний» термин среди следующих: а) отрезок; б) интервал; в) модуль; г) луч.
|
| 3. Алгебраическое уравнение n-степени: а) всегда имеет n корней; б) имеет не более n корней; в) имеет не менее n корней; г) не имеет корней.
| 3. Алгебраическое уравнение n-степени: а) всегда имеет n корней; б) имеет не более n корней; в) имеет не менее n корней; г) не имеет корней.
|
| 4. Ортоцентр треугольника - это точка пересечения: а) медиан; б) высот; в) биссектрис; г) серединных перпендикуляров.
| 4. Ортоцентр треугольника - это точка пересечения: а) медиан; б) высот; в) биссектрис; г) серединных перпендикуляров.
|
| 5. Вадим участвует в соревнованиях по бегу. В какой- то момент оказалось, что впереди него бежит треть всех участников, сзади — половина, а рядом с ним никого нет. Сколько человек участвуют в забеге? а) 5; 6)12; в) 6; г)18.
| 5. Вадим участвует в соревнованиях по бегу. В какой- то момент оказалось, что впереди него бежит треть всех участников, сзади — половина, а рядом с ним никого нет. Сколько человек участвуют в забеге? а) 5; 6)12; в) 6; г)18.
|
| 6. Раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций можно составить из заданных объектов - это: а) арифметика; б) тригонометрия; в) комбинаторика; г) геометрия.
| 6. Раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций можно составить из заданных объектов - это: а) арифметика; б) тригонометрия; в) комбинаторика; г) геометрия.
|
| 7. Какое из этих чисел не равно остальным? а) в) 30% от 1; г) 0,3.
| 7. Какое из этих чисел не равно остальным? а) в) 30% от 1; г) 0,3.
|
| 8. Сколько осей симметрии имеет квадрат? а) 4; 6)6; в) 8; г) 2.
| 8. Сколько осей симметрии имеет квадрат? а) 4; 6)6; в) 8; г) 2.
|
| 9. Баранка имеет форму: а) эллипсоида; б) тора; в) цилиндра; г)многогранника.
| 9. Баранка имеет форму: а) эллипсоида; б) тора; в) цилиндра; г)многогранника.
|
| 10. Лобачевский Николай Иванович в 1826 г. сделал сообщение об открытии новой а) формулы; б) теоремы; в) геометрии; г) гипотезы.
| 10. Лобачевский Николай Иванович в 1826 г. сделал сообщение об открытии новой а) формулы; б) теоремы; в) геометрии; г) гипотезы.
|

 Получите свидетельство
Получите свидетельство Вход
Вход












 Внеклассное мероприятие по математике: «Кто хочет стать отличником» (24.26 KB)
Внеклассное мероприятие по математике: «Кто хочет стать отличником» (24.26 KB)
 0
0 342
342 16
16 Нравится
0
Нравится
0


