Внеклассное занятие по математике.
Тема: «Геометрия ножниц. Задачи на разрезание и складывание фигур»
Автор: Сорокина Любовь Васильевна, учитель математики высшей квалификационной категории.
Занятие можно проводить для обучающихся в 7-9 классах.
Федеральные государственные образовательные стандарты поставили на первое место не предметный, а личностный результат. На первый план выходят не столько сами знания, сколько средства и инструменты их самостоятельного приобретения, углубления и обновления знаний, независимо от того, к какой предметной области они принадлежат.
Для учителя работа по федеральным государственным образовательным стандартам - это переход от передачи знаний к созданию условий для активного познания и получения детьми практического опыта.
Для учеников это - переход от пассивного усвоения информации к активному ее поиску, критическому осмыслению, использованию на практике.
Актуальность темы:
Трудно не согласиться с тем, что геометрические задачи всегда вызывают у обучающихся наибольшие затруднения. Как результат – многие выпускники плохо решают задачи модуля «Геометрия» на итоговой аттестации. На мой взгляд, причин создавшегося положения можно выделить немало, как субъективных, так и объективных. Вот некоторые из них: слабая внутренняя (познавательная) мотивация, отсутствие интереса при решении геометрических задач, неумение выделять главное в задаче, плохо развитое пространственное воображение, отсутствие понимания связи приобретенных знаний, умений и их использования в практической деятельности и др. Мне кажется, что большую помощь в решении этих проблем могут оказать задачи на построение. Эти задачи обычно не допускают стандартного подхода к ним и формального восприятия их обучающимися. Однако, этим задачам в школьном курсе геометрии уделяется мало внимания и времени, в итоге всё сводится лишь к рассмотрению простейших задач на построение, хотя, важность конструктивных задач в развитии логического мышления, эстетического воспитания и прикладной направленности трудно переоценить. Эти задачи полезны и для развития пространственного видения, что необходимо при изучении стереометрии в старших классах.
Поэтому, просто необходимо на внеклассных занятиях рассматривать задачи на построение, добавив, в обязательном порядке, задачи на разрезание и складывание фигур, а также задачи на клетчатой бумаге. Даже эти, на первый взгляд, несложные задачи ставят в тупик выпускников, потому что они не владеют приемами решения задач, у них недостаточно сформированы геометрические представления о площади и ее свойствах. Задачи на разрезание и складывание, задачи на клетчатой бумаге призваны исправить эти недостатки, кроме того, они развивают практические навыки, повышают интерес к геометрии и математике, развивают фантазию, логику, формируют и совершенствуют исследовательские умения и навыки.
Приведу пример одного из внеклассных занятий по геометрии, которое было проведено в 7 классе.
Цели:
знакомство обучающихся с различными задачами на разрезание и складывание фигур;
нахождение площадей фигур на клетчатой бумаге;
формирование пространственного воображения обучающихся;
активизации поисково-познавательной деятельности обучающихся;
Задачи:
рассмотреть различные способы решения геометрических задач на разрезание и складывание фигур на плоскости;
познакомить с задачами на клетчатой бумаге и их решением;
развивать изобретательность и нестандартность мышления учащихся;
развивать интерес к практическому использованию знаний в конструировании.
Ход занятия.
Ребята, вы любите приключения? Вячеславу Викторовичу Произволову, автору увлекательной книги «Задачи на вырост», принадлежат слова: «Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение». Я предлагаю вам сегодня пережить интереснейшее приключение.
Посмотрите на картины известных и неизвестных художников. Как вы думаете, что их объединяет?







Попробуйте пофантазировать и предположить, решением каких задач могут быть заняты персонажи картин? Возможно, что они решают задачи на построение. А нам знакомы такие задачи? Какие инструменты можно использовать при решении классических задач на построение?
Но мы сегодня будем решать несколько другие задачи. А что это за задачи, догадайтесь сами. Известно, что с этими задачами, очевидно, столкнулся ещё первобытный человек, когда пытался раскроить шкуру убитого зверя, чтобы сшить себе одежду. Решения многих простых подобных задач были найдены ещё древними греками. Догадались, о каких задачах идет речь?
Да, конечно, речь идет о задачах на разрезание. Задачи на разрезание или на перекраивание фигур возникли в глубокой древности. Уже в VII—V вв. до н.э. в Индии в книге «Правила веревки» рассматриваются задачи на перекраивание фигуры, состоящей из двух квадратов, в равновеликий ей квадрат и перекраивание прямоугольника в квадрат. Первый письменный источник с подобными задачами относится к Х веку – это фрагменты трактата персидского астронома Абул-Вефа, жившего в Багдаде. Профессиональные математики всерьёз занялись задачами на разрезание ближе к середине XIX века.
Отложим в сторону циркуль и возьмем ножницы. Кроить, вырезать, соображать – вот что требуется при решении задач по геометрии ножниц.
Задачи на разрезание и перекраивание фигур.
Задача №1.
Перекроите фигуру, состоящую из двух квадратов, в равновеликий ей квадрат.
(Для решения задачи ребятам надо найти ответ на вопрос: какие фигуры являются равновеликими? Они находят ответ либо в математическом справочнике, либо в интернете).
Решение. Разрезать по диагонали каждый квадрат. Диагонали будут являться сторонами получившегося квадрата.
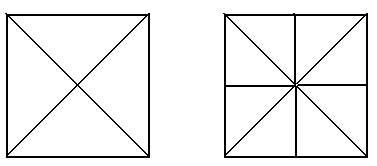
Задача №2.
Разрежьте прямоугольник, длина которого равна 9 клеток, а ширина 4, на две равные части так, чтобы из них можно было сложить квадрат.
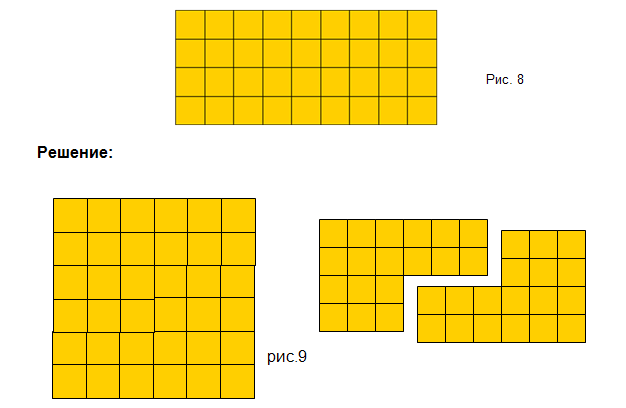
Решение.


Задача №3.
Постройте прямоугольник со сторонами 2 см и 5 см. Разрежьте прямоугольник по диагонали. Сложите из получившихся частей треугольник.
Можно ли из этих частей сложить еще один треугольник, не равный данному? Если можно, то сложите еще один треугольник.
Задача №4.
Постройте прямоугольный треугольник, у которого две стороны равны. Разрежьте его на три неравные части, из которых можно было бы составить два равных квадрата.
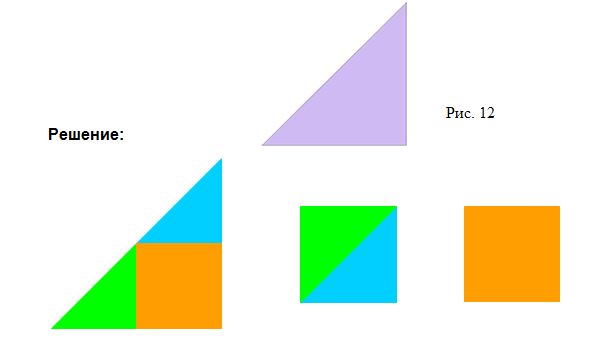 Решение.
Решение. 
Задача №5 .
Разрежьте квадрат на 3 части, из которых можно сложить треугольник с 3 острыми углами и тремя различными сторонами.
Решение представлено на рисунке.
Задачи на нахождении площади фигуры на клетчатой бумаге.
Выпускники сдают ЕГЭ, предусматривающий решение интересных, нестандартных задач из курса геометрии. Многие из них можно решить, не используя формулы, а применяя метод разрезания и перекраивания. Рассмотрим одну такую задачу.
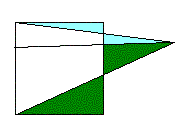
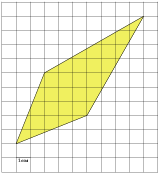
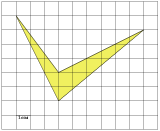
Задача №5 . Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
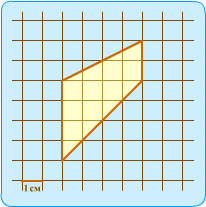 Ребята сначала предлагают свои решения.
Ребята сначала предлагают свои решения.
А теперь предлагаю рассмотреть один из способов решения. Вы не знаете формулы нахождения площади трапеции, но обладаете хорошим воображением. Способ сродни решению головоломки - как разрезать плоскую фигуру на части, чтобы из этих частей, используя каждую из них одинаковое число раз, сложить прямоугольник? Затем, просто посчитать количество клеточек внутри прямоугольника, и разделить на число повторов деталей заданной фигуры. Смотрите.
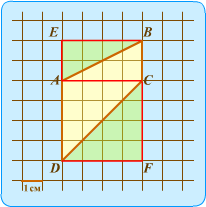
Проводим дополнительную линию AC и "разрезаем" трапецию на две части, как в решении вторым способом. Проводим дополнительные линии и строим вершины E и F, как в решении третьим способом. Убеждаемся в том, что получившиеся зеленые и желтые треугольники попарно равны (подсчетом клеточек на соответствующих сторонах). Значит, для построения прямоугольника детали заданной фигуры использованы 2 раза, один комплект желтый, второй - зеленый. Считаем общее количество клеточек в закрашенном прямоугольнике. Получается 24. Делим на 2. 24/2 = 12. Ответ: 12.
Рассмотрим еще один способ решения задачи. Способ требует тех же самых знаний, что и предыдущий, только немножко иного взгляда на картинку. Теперь мы будем не "разрезать" нашу трапецию на части, а "вырезать" её из прямоугольника, стороны которого проходят по линиям сетки через вершины заданной трапеции.
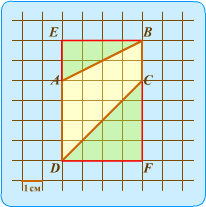
Проводим горизонтальные линии через вершины В и D, продолжаем вертикальные линии AD и ВС до пересечения с горизонтальными. Точки пересечения обозначим символами E и F. Получили прямоугольник DEBF со сторонами DE = 6 и DF = 4, его площадь 6×4 = 24. Чтобы получить искомую площадь трапеции, нужно из площади этого прямоугольника вычесть площади (зелёных) треугольников AEB и DFC.
SAEB = AE·EB/2 = 2·4/2 = 4 и SDFC = DF·FC/2 = 4·4/2 = 8.
Следовательно, площадь трапеции равна S = 24 − 4 − 8 = 12.
Рассмотрите задачи из открытого банка заданий ЕГЭ, предложите их решения.

Наше приключение подходит к концу. На следующем занятии мы продолжим решение задач на разрезание, перекраивание, нахождение площадей фигур на клетчатой бумаге, добавим еще фигуры на координатной плоскости. Я надеюсь, что мир наглядной геометрии вас увлек.
Предлагаю вам к следующему занятию выполнить одно из заданий:
найдите или придумайте сами задачу на разрезание фигур;
подберите и решите задачи из открытого банка заданий ЕГЭ по математике на нахождение площадей фигур, изображенных на клетчатой бумаге.
Используемые ресурсы:
http://davaiknam.ru/texts/997/996675/996675_html_2dd4ed2a.jpg
http://www.fabulantes.com/wp-content/uploads/2012/09/Newton.jpg
http://knoow.it/uploads/cache/pins/2012/10/mathematics-wikipedia-the-free-encyclopedia_213124562194258051-220x.jpeg
https://im1-tub-ru.yandex.net/i?id=201e70f7ce77e7dd669e1e374e7faa16&n=33&h=190&w=141
http://cs622529.vk.me/v622529214/3d2f6/IroRA9787Dc.jpg
http://soi.com.vn/wp-content/images/2011/11/urania-Johann-Heinrich-Tischbein-1782.jpg
http://sigils.ru/signs/img/zirkul.jpg


 Получите свидетельство
Получите свидетельство Вход
Вход












 Решение.
Решение. 
 Ребята сначала предлагают свои решения.
Ребята сначала предлагают свои решения.














 Внеклассное занятие по математике «Геометрия ножниц. Задачи на разрезание и складывание фигур» (0.67 MB)
Внеклассное занятие по математике «Геометрия ножниц. Задачи на разрезание и складывание фигур» (0.67 MB)
 0
0 4406
4406 661
661 Нравится
0
Нравится
0


