Глазачева Г.А.
учитель МАОУ «СОШ №2»
г.Первоуральск
Входная диагностика уровня знаний и умений учащихся
на начальном этапе обучения математике в 8 классе
Математику уже затем учить надо,
что она ум в порядок приводит.
М.В. Ломоносов, 1711-1765
русский учёный-естествоиспытатель, «универсальный человек»
Математика — королева и служанка наук.
Э.Т. Белл, 1883-1960
американский математик, писатель-фантаст
В курсе математики 8 класса можно выделить следующие основные содержательные линии: арифметика, элементы алгебры, наглядная геометрия.
Содержание линии «Арифметика» служит фундаментом для дальнейшего изучения учащимися математики и смежных дисциплин, способствует развитию не только вычислительных навыков, но и логического мышления, формированию умения пользоваться алгоритмами, способствует развитию умений планировать и осуществлять деятельность, направленную на решение различных задач, а также приобретению практических навыков, необходимых в повседневной жизни.
Содержание линии «Элементы алгебры» систематизирует знания о математическом языке, показывая применение букв для обозначения чисел и записи свойств арифметических действий, а также для нахождения неизвестных компонентов арифметических действий.
Содержание линии «Наглядная геометрия» способствует формированию у учащихся первичных представлений о геометрических абстракциях реального мира, закладывает основы правильной геометрической речи, развивает образное мышление и пространственные представления. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства [1].
Многие учащиеся не владеют или не могут овладеть вычислительными навыками, допуская различные вычислительные ошибки. Причинами невысокой вычислительной культуры учащихся могут быть: низкий уровень развития памяти и внимания, мыслительных и личностных качеств; отсутствие контроля со стороны родителей за выполнением домашнего задания; недостаточный уровень подготовки по математике на этапе начального общего образования и, как следствие, на этапе основного общего образования. Приступая к организации обучения математике в 8 классе, учителю необходимо в очередной раз определить у учащихся уровень остаточных знаний и умений, применяемых на базовом уровне при решении простейших арифметических, алгебраических и геометрических заданий.
С целью организации входной диагностики вычислительных умений и остаточных базовых знаний учащихся 8 класса по отдельным темам курса математики 5-6 класса, алгебры и геометрии 7 класса был разработан тест в 4-х вариантах на основе 9 из 13 моделей заданий ВПР-2024 [2].
На основе результатов теста учитель может: определить не только уровень вычислительных умений, но и уровень скоростных качеств учащихся; организовать коррекционную работу по ликвидации выявленных пробелов в базовых знаниях и умениях;
использовать дифференцированный подход в дальнейшем обучении.
Проверяемые предметные знания и умения: умение выполнять арифметические действия с рациональными числами устно или письменно, порядок их выполнения; знание и умение применять алгоритм решения линейного уравнения, раскрывать скобки, приводить подобные слагаемые; применять логические рассуждения, исходя из условия задачи; умение решать простейшие текстовые задачи на проценты из реальной жизни; умение перейти от одних единиц измерения скорости к другим; знание и умение применять понятия, связанные с линейной функцией: уравнение и график; знать и распознавать на рисунке геометрические понятия, применять их определение, свойства и признаки при решении текстовых задач.
В процессе выполнения теста учащиеся применяют: читательскую и математическую грамотность, навыки устного и письменного счета с рациональными числами,
теоретические знания на базовом уровне по некоторым темам курса математики 5-6 класса, алгебры и геометрии 7 класса.
Время выполнения теста: 35-45 мин.
Структура теста:
задания №1- 2 действия 1-й и 2й ступеней с обыкновенными дробями: приведение дробей к общему знаменателю, сокращение дроби – математика 5-6 класс;
задания №2- 2 действия 1-й и 2й ступеней с десятичными дробями – математика 5-6 класс;
задания №3 – решение линейного уравнения: раскрытие скобок, перенос слагаемых, приведение подобных, действия с положительными и отрицательными числами – алгебра 7 класс;
задания №4 – применение логических рассуждений, исходя из условия текстовой задачи: выбор номера верного утверждения - математика 5-6 класс;
задания №5 – текстовая задача на понимание скорости: переход к другим единицам измерения длины, времени, скорости - математика 5-6 класс;
задания №6 – решение текстовой задачи на проценты (распознавание и применение ключевой задачи на проценты: 1) сколько процентов составляет одна величина от другой, или 2) нахождение числа по величине его процентов) - математика 5-6 класс;
задания №7 – вычисление коэффициента в уравнении линейной функции по координатам точки, через которую проходит график этой функции - алгебра 7 класс;
задания №8 – знание и умение находить по рисунку на клетчатой бумаге геометрическую величину: 1) расстояние от точки до прямой, или 2) медиану (высоту) треугольника – геометрия 7 класс;
задания №9 – умение составить рисунок к геометрической задаче, отметить данные и искомую величину, обнаружить связь между ними, применить теоретические знания: 1) понятие внешнего угла, биссектрисы треугольника, свойство параллельных прямых, или 2) понятие высоты треугольника, признака угла 30 градусов в прямоугольном треугольнике – геометрия 7 класс.
Задания №№1-5, 7, 8 оцениваются 1 баллом; задания №№6,9 - 2 баллами, т.к. при выполнении требуется время на осознанное прочтение, установление причинно-следственных связей, выбор и применение теоретических знаний.
Максимальный балл: 11 баллов.
Критерии оценивания:
4-6 – «3» (с 36-55%) – «удовлетворительно»,
7-9 – «4» (с 64-82%) – «хорошо»,
10-11 – «5» (с 91-100%) – «отлично».
ТЕСТ
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | |
| 1. (1 балл) Найдите значение выражения и внесите полученный ответ в виде несократимой дроби в отведенное поле, используя в качестве дробной черты знак « / » : | ||||
|
|
|
|
| |
| 2. (1 балл) Найдите значение выражения и внесите полученный ответ в виде десятичной дроби в отведенное поле: | ||||
|
|
|
|
| |
| 3. (1 балл) Решите уравнение и внесите полученный числовой ответ в отведенное поле: | ||||
|
|
|
|
| |
| 4. (1 балл) Выберите верные утверждения, исходя из условия, и запишите их номера в отведенное поле без пробелов и запятых: | ||||
| Оля младше Алисы, но старше Иры. Лена не младше Оли. 1) Алиса старше Иры. 2) Среди указанных четырёх девочек Ира самая младшая. 3) Алиса и Ира одного возраста. 4) Алиса и Оля одного возраста. | Оля старше Светы, но младше Юли. Маша не старше Оли. 1) Среди указанных четырёх девочек нет никого старше Юли. 2) Маша и Юля одного возраста. 3) Юля старше Светы. 4) Юля и Оля одного возраста | Точилка стоит столько же, сколько карандаш и линейка вместе, а линейка дороже карандаша. 1) Точилка дороже карандаша. 2) Две линейки стоят дороже точилки. 3) Карандаш дороже линейки. 4) Линейка дороже точилки. | Тетрадь стоит столько же, сколько ручка и линейка вместе, а линейка дороже ручки. 1) Ручка дороже тетради. 2) Тетрадь дороже линейки. 3) Ручка дешевле линейки. 4) Две линейки стоят дешевле тетради. | |
| 5. (1 балл) Решите задачу и внесите полученный числовой ответ в отведенное поле: | ||||
| Самолёт летит со скоростью 324 км/ч. Сколько метров он преодолевает за одну секунду? | Самолёт летит со скоростью 954 км/ч. Сколько метров он преодолевает за одну секунду? | Самолёт летит со скоростью 522 км/ч. Сколько метров он преодолевает за одну секунду? | Самолёт летит со скоростью 792 км/ч. Сколько метров он преодолевает за одну секунду? | |
| 6. (2 балла) Решите задачу и внесите полученный числовой ответ в отведенное поле: | ||||
| Футболка в марте стоила 800 рублей. В июле стала стоить 600 рублей. На сколько процентов была снижена цена футболки? | Футболка в марте стоила 800 рублей. В июле стала стоить 680 рублей. На сколько процентов была снижена цена ? | Кофеварку уценили на 9%, при этом она стала стоить 7371 рубль. Сколько рублей стоила кофеварка до уценки? | Кофеварку уценили на 15%, при этом она стала стоить 5100 рублей. Сколько рублей стоила кофеварка до уценки? | |
| 7. (1 балл) Выполните задание и внесите полученный числовой ответ в отведенное поле: | ||||
| График функции проходит через точку с координатами (4; - 7). Найдите значение b. | График функции
проходит через точку с координатами (− 4; – 5). Найдите значение b. | График функции
проходит через точку с координатами (5; – 12). Найдите значение b. | График функции
проходит через точку с координатами (- 5; 12). Найдите значение b . | |
| 8. (1 балл) Выполните задание и внесите полученный числовой ответ в отведенное поле: | ||||
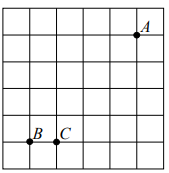
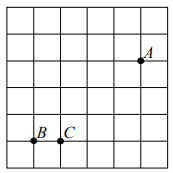
| На клетчатой бумаге с размером клетки 1×1 отмечены точки А, В и С. Найдите расстояние от точки A до прямой ВС.
| На клетчатой бумаге с размером клетки 1×1 отмечены точки А, В и С. Найдите расстояние от точки A до прямой ВС.
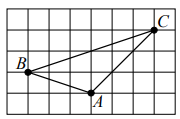
| На клетчатой бумаге с размером клетки 1×1 нарисован треугольник ABC. Найдите медиану к стороне BC.
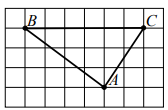
| На клетчатой бумаге с размером клетки 1×1 нарисован треугольник ABC. Найдите высоту к стороне BC.
| |
| 9. (2 балла) Решите задачу и внесите полученный числовой ответ в отведенное поле: | ||||
| Биссектриса внешнего угла при вершине В треугольника ABC параллельна стороне АС. Найдите величину угла САВ, если ∠ АВС =34 °. Ответ дайте в градусах.
| Биссектриса внешнего угла при вершине В треугольника ABC параллельна стороне АС. Найдите величину угла САВ, если ∠ АВС =40 °. Ответ дайте в градусах. | В прямоугольном треугольнике ABC с прямым углом C проведена высота CD. Найдите величину угла A, если DB = 8, а BC =16. Ответ дайте в градусах. | В прямоугольном треугольнике ABC с прямым углом C проведена высота CD. Найдите величину угла В, если СD = 6, а АC =12. Ответ дайте в градусах. | |
КЛЮЧ К ТЕСТУ
| Вариант 1 | Вариант 2 | Вариант 3 | Вариант 4 | |||||||
| № | ОТВЕТ | № | ОТВЕТ | № | ОТВЕТ | № | ОТВЕТ | |||
| 1 | 4/3 | 1 | 5/3 | 1 | 14/5 | 1 | 3/2 | |||
| 2 | 7,78 | 2 | 26,3 | 2 | 6,1 | 2 | 0,7 | |||
| 3 | х= 3 | 3 | х= 5 | 3 | х= 4,5 | 3 | х= -5 | |||
| 4 | 12 | 4 | 13 | 4 | 12 | 4 | 23 | |||
| 5 | 90 м/c | 5 | 265 м/c | 5 | 145 м/c | 5 | 220 м/c | |||
| 6 | 25 % | 6 | 15 % | 6 | 8100 руб. | 6 | 6000 руб. | |||
| 7 | b= -12,2 | 7 | b= 0,2 | 7 | b= 2,5 | 7 | b= -2,5 | |||
| 8 | 4 | 8 | 3 | 8 | 2 | 8 | 3 | |||
| 9 | 73 0 | 9 | 70 0 | 9 | 30 0 | 9 | 60 0 | |||
Источники информации
-
file:///C:/Users/User/Desktop/matematika_8_kl.pdf Рабочая программа по математике в 8 классе. Составитель: Коленченко О.Н. г.Владивосток
-
https://vprklass.ru/ ВПР КЛАСС : Варианты ВПР с ответами

 Получите свидетельство
Получите свидетельство Вход
Вход












 Входная диагностика уровня знаний и умений учащихся на начальном этапе обучения математике в 8 классе (тест) (68.79 KB)
Входная диагностика уровня знаний и умений учащихся на начальном этапе обучения математике в 8 классе (тест) (68.79 KB)
 0
0 190
190 6
6 Нравится
0
Нравится
0


