Урок в 9 классе по теме: «Преобразование графиков: симметрия относительно осей координат»
Учитель: Шарова С. Г., МБОУ «Гимназия» городского округа г. Урюпинск Волгоградской области
Тип урока: открытие нового знания.
Основные цели:
Метапредметные:
Тренировать умение фиксировать свое затруднение, выявлять причину его возникновения.
Тренировать умение ставить цель своей деятельности и планировать работу по реализации поставленной цели.
Тренировать умение работать в парах и группах.
Предметные:
Сформировать умение выполнять следующие преобразования графиков: симметрия относительно осей координат.
Сформировать умение применять данные преобразования графиков для построения графиков функций вида: y = f(–x), y = –f(x), y = –f(–x) из графика y = f(x).
Закрепить умение решать уравнения, содержащие знак модуля.
Ход урока
Мотивация к учебной деятельности
- Здравствуйте, ребята! Сегодня мы продолжим знакомство с преобразованиями графиков функций, которые позволяют строить графики более сложных функций оптимально.
- Как вы понимаете высказывание американского педагога Дайан Силверс Рейвич: «Человек, который знает «как», всегда найдёт работу, а человек, который знает «почему», будет его начальником». (слайд 2)
Возможный ответ: Перед человеком, задумывающимся о причинах тех или иных явлений, способов действий, открывается больше возможностей. Он может сделать или организовать что-то более продуктивно, более эффективно.
- Ребята, я вам желаю интересной работы на уроке: уверена, вы сегодня найдете интересные способы для достижения цели и будете пользоваться ими в дальнейшем осознанно.
- Подготовку к открытию нового начнем с проверки домашнего задания. Сейчас каждой группе будет предложен подробный образец выполнения задания из домашней работы. Организатор группы фиксирует все затруднения, возникшие у членов группы. В группах вы выявляете причины возникших затруднений.
- Не забудьте! При проверке домашнего задания вам нужно составить список эталонов, которыми пользовались при выполнении заданий.
2. Самостоятельная деятельность и организация учебного затруднения.
(Идет работа в группах)
Домашнее задание.
Задание №1.
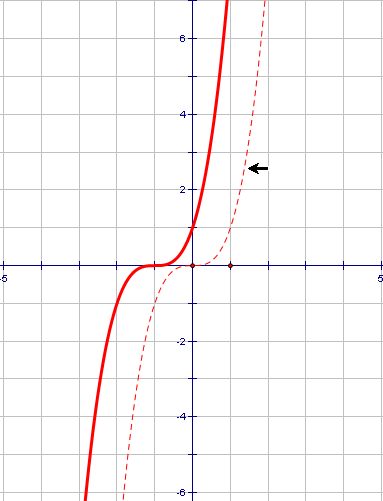
a). Построить график функции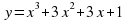 .
.
Решение. Для того чтобы построить график данной функции, необходимо преобразовать правую часть, воспользовавшись формулой 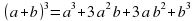 .
.
Получим 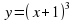 . Сдвинем график
. Сдвинем график 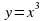 вдоль оси абсцисс на 1 единицу влево.
вдоль оси абсцисс на 1 единицу влево.

0
-1
b) Построить график функции 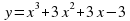
Решение. Для того чтобы построить график данной функции необходимо преобразовать правую часть, выделив куб суммы. Получим 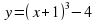 .
.
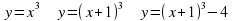 .
.
Сдвиг по оси абсцисс влево на 1 единицу и вниз по оси ординат на 4 единицы.


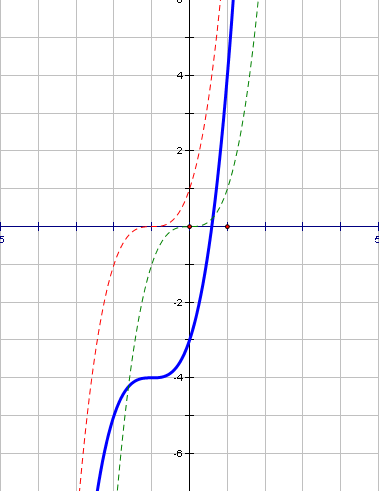
0
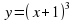
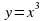
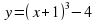
в) Построить график функции 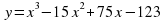 .
.
Решение. Для того чтобы построить график данной функции необходимо преобразовать правую часть, выделив куб разности:
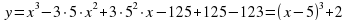 .
.
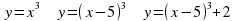 .
.
Сдвиг по оси абсцисс вправо на 5 единиц и вверх по оси ординат на 2 единичных отрезка.


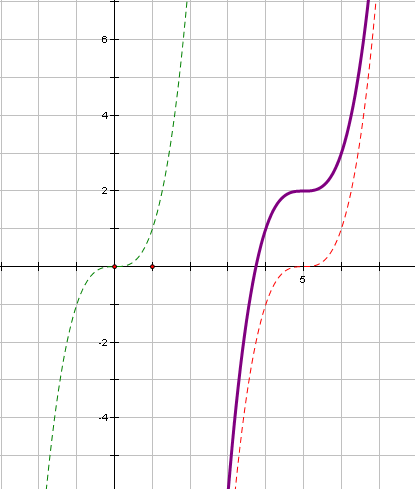
0
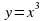
Задание №2.
Построить график функции
.
Построить график функции
.
Решение.
Для того чтобы построить график функции
, необходимо выполнить сдвиг вспомогательного графика функции
вдоль оси OY вверх на 3 единицы.
Для того чтобы построить график функции
, необходимо выполнить сдвиг вспомогательного графика функции
вдоль оси OX влево на 1 единицу, вдоль оси OY вверх на 3 единицы.
а)
б)
5
-1
0
Задание №3.
Построить график функции
.
Построить график функции
.
Решение.
Чтобы построить график
, увеличим ординаты вспомогательного графика
в 2 раза (k1), не меняя область определения ),то есть растянем график
от оси OX в 2 раза.
Чтобы построить график
, уменьшим абсциссы вспомогательного графика
в четыре раза (k1), не меняя область значения функции ), то есть сожмем график
к оси OY в 4 раза.
После проверки домашнего задания в группах.
Возможные ответы учащихся.
При выполнении заданий повторяли:
приемы построения графиков функций с помощью сдвигов вдоль осей координат.
Приемы построения графиков функций с помощью сжатия или растяжения вдоль осей координат.
-Задание на пробное действие.
- Ребята, при выполнении задания №3 вы работали с графиком функции .
- Как вы строили график данной функции?
| x | 0 | 1 | 4 | 9 |
| y | 0 | 1 | 2 | 3 |
Составили таблицу значений функции
4
1
0
Теперь я предлагаю вам следующее задание:
Постройте графики функций:
; б)
; в)
, преобразовав график
.
Учащиеся самостоятельно пытаются построить графики заданных функций. Время на выполнение заданий ограничено.
- Обсудите в группах, какие затруднения могут быть?
Одна из групп отвечает, остальные уточняют, дополняют.
Возможные варианты ответов:
Я не могу построить график данной функции.
Я не могу объяснить, что мой ответ верный.
Я не могу проанализировать, как изменится область определения и множество значений функций
и т. д.
3.Выявление места и причины затруднения.
-Посовещавшись в группах в течение 30 секунд, ответьте на вопрос:
Почему возникло затруднение?
Одна из групп отвечает, остальные уточняют, дополняют.
Возможные варианты ответов:
– Необходимо было построить графики функций, содержащие знак корня, применяя преобразования. Затруднение возникло в определении преобразований. Причина в том, что мы не знаем пока, какое преобразование можно применить в тех случаях, когда функция содержит знак минус перед данной функцией, знак минус перед аргументом данной функции и знак минус одновременно перед данной функцией и перед ее аргументом.
4. Построение проекта выхода из затруднения.
- Посовещавшись в группах в течение 30 секунд:
1) сформулируйте цель дальнейшей деятельности;
2) сформулируйте тему урока.
Одна из групп озвучивает результат обсуждения, остальные уточняют, дополняют при необходимости.
Возможный вариант ответа:
Цель: Узнать, какие преобразования графика функции у = f(x) необходимо выполнить, чтобы получить графики функций у = –f(x), у = f(–x), у = –f(–x).
Тема урока: «Преобразования графиков функций».
– Составьте в группах план ваших действий.
Учащиеся работают в группах, составляют план действий.
Возможный вариант ответа:
Выполнить задания, предложенные учителем,
Проанализировать результаты.
Сформулировать правило.
Сравнить его с эталоном.
5.Реализация построенного проекта
- Итак, вернемся к заданию
Постройте графики функций:
а); б)
; в)
, используя таблицу значений функции, и пронаблюдайте, как расположены построенные графики по отношению к графику
относительно осей координат, начала отсчета. Обобщите сделанные вами наблюдения и составьте правила построения таких функций. Сопоставьте свои выводы с выводами на слайдах.
Возможный вариант ответа:
а)
0
;
б)
0
в)
0
а) Преобразование y = f(x) y= –f(x) изменяет все ординаты точек графика на противоположные
при фиксированных значениях абсцисс. Область определения функции
D (f) = [0; +∞), а область значений E(f) = (–∞; 0].
Значит, график функции у = – f(x) можно получить из графика у = f(x) с помощью осевой симметрии относительно оси абсцисс.
Б) Преобразование y = f(x) y= f(–x) изменяет все абсциссы точек графика на противоположные
при фиксированных значениях ординат. То есть область определения функции
D (f) = (–∞; 0], а область значений E (f) = [0; +∞).
Значит, график функции у = f(–x) можно получить из графика у = f(x) с помощью осевой симметрии относительно оси ординат.
В) Последовательное применение рассмотренных выше двух преобразований:
y = f(x) y = – f (–x) меняет абсциссы и ординаты точек графика на противоположные. Область определения функции D (f) = (–∞; 0], а область значений E(f) = (–∞; 0].
Значит, график функции у = – f(–x) можно получить из графика у = f(x) с помощью центральной симметрии относительно начала координат.
Учащиеся сравнивают свои правила с эталоном на слайде:
Случаи преобразования графика функции
Симметрия относительно оси абсцисс
График функции у = – f(x) можно получить из графика у = f(x) с помощью осевой симметрии относительно оси абсцисс.
Симметрия относительно оси ординат
График функции у = f(–x) можно получить из графика у = f(x) с помощью осевой симметрии относительно оси ординат.
Симметрия относительно начала координат
График функции у = – f(–x) можно получить из графика у = f(x) с помощью центральной симметрии относительно начала координат
Случаи преобразования графика функции
Симметрия относительно оси абсцисс
График функции у = – f(x) можно получить из графика у = f(x) с помощью осевой симметрии относительно оси абсцисс.
Симметрия относительно оси ординат
График функции у = f(–x) можно получить из графика у = f(x) с помощью осевой симметрии относительно оси ординат.
Симметрия относительно начала координат
График функции у = – f(–x) можно получить из графика у = f(x) с помощью центральной симметрии относительно начала координат
– Удалось преодолеть затруднение?
− Что теперь необходимо сделать?
6. Первичное закрепление во внешней речи
- Выполните задание: постройте график функции у = f(–x), если f(x) =.
Работа выполняется фронтально.
Решение:
Для того чтобы построить график функции , можно преобразовать правую часть, выделив квадрат двучлена:
.
Для построения графика функции у = f(–x) необходимо построить график f(x) = и применить к нему следующее преобразование: симметрию относительно оси ординат: у = f(–x) =
.
-Выполните задание:
Постройте графики функций у = – f(x), у = – f(–x), если
Задание выполняется в парах, по вариантам. Проверка осуществляется по пробному образцу.
Пробный образец.
Для построения графиков функций у = – f(x), у = – f(–x) необходимо построить график и применить к нему следующие преобразования:
Симметрию относительно оси абсцисс: у = – f(x) =;
Симметрию относительно начала координат: у = – f(–x) =
Y
– f(–x) =
– f(x) =
x
После самопроверки проводится рефлексия: выясняется, есть ли ошибки, если есть, то проговаривается, как надо было выполнить задание.
7.Самостоятельная работа с самопроверкой по эталону
- Мы шли с вами по плану, предложенному вами:
Выполнить задания, предложенные учителем,
Проанализировать результаты.
Сформулировать правило.
Сравнить его с эталоном.
-Что дальше необходимо сделать?
- С какой целью будете выполнять самостоятельную работу?
Возможный вариант ответа:
Понять полностью ли разобрались в новой теме, нет ли затруднений.
Для самостоятельной работы учащимся предлагается задание:
Постройте графики функций у = –f(x), у = f(–x), у = –f(–x), если f(x)=
Учащиеся выполняют самостоятельную работу и проводят самопроверку по эталону для самопроверки.
Подробный образец.
f (x)= . Для построения графиков функций у = –f(x), у = f(–x), у = –f(–x) необходимо построить f (x) =
и применить к нему следующие преобразования:
симметрию относительно оси абсцисс: у = –f(x) =
;
симметрию относительно оси ординат: у = f(–x) =
;
симметрию относительно начала координат: у = –f(–x) =
.
–f(–x) =
f (–x) =
–f(x) =
f (x) =
X
Y
Проанализируйте в группах результаты выполнения самостоятельной работы.
Назовите, в каких местах и почему возникли затруднения.
Организаторы групп озвучивают результаты анализа работ.
8. Включение в систему знаний и повторение.
Решите уравнения:
;
;
;
;
.
Решение.
Не имеет решения, так как по определению
.
Уравнение
не имеет решения, так как левая часть равенства по определению модуля числа неотрицательна, а правая – по условию и определению модуля неположительна. При
выражение
.
=2
⇔⇔⇔
.
9. Рефлексия деятельности на уроке
- Ребята, что необходимо сделать в конце урока?
Возможный вариант ответа:
Проанализировать свою работу.
Группы работают с карточкой.
Определить новые знания, которые открыты на уроке.
Сформулируйте цель, которая стояла перед вами.
Определите, достигнута ли цель.
Перечислите средства и способы, которые вам помогли достичь цели.
Оцените деятельность группы и каждого участника группы на уроке.
Сформулируйте неразрешенные затруднения на уроке, если они есть.
Учащиеся обсуждают работу на уроке, организаторы озвучивают результаты анализа деятельности групп.
- А теперь каждый проанализируйте свою работу.
Учащиеся заполняют индивидуальные карточки
| Понятия и способы действий | Знаю | Получилось применить |
| Преобразование графика функции с помощью симметрии относительно оси абсцисс. |
|
|
| Преобразование графика функции с помощью симметрии относительно оси ординат. |
|
|
| Преобразование графика функции с помощью симметрии относительно начала координат. |
|
|
Домашнее задание
Постройте графики функций у = –f(x), у = f(–x), у = –f(–x), если:
,
,
.
Повторить эталоны.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Урок в 9 классе по теме: «Преобразование графиков: симметрия относительно осей координат» (199.69 KB)
Урок в 9 классе по теме: «Преобразование графиков: симметрия относительно осей координат» (199.69 KB)
 0
0 839
839 104
104 Нравится
0
Нравится
0


