Урок-семинар по математике в 11 классе по теме: «Производная функции. Исследование функции с помощью производной» разработала
Зезюлина Лариса Леонидовна, учитель математики МБОУ Витемлянская СОШ
Погарского района Брянской области.
Цели :
Общеобразовательные - проверка сформированности у учащихся определения производной, физического и геометрического смысла производной, устанавливать характер изменения функции по знаку производной, выявлять точки, подозрительные на экстремум, использовать понятии е производной для исследования свойств функции;
Развивающие – установить, могут ли учащиеся применять метод дифференциального исчисления для решения прикладных задач, установить , могут ли учащиеся выделять этапы в решении прикладных задач;
Воспитательные – проверить сформированность качеств знаний: прочность, глубина, оперативность мышления.
I
Вопросы к классу с комментариями учителя
1.Дайте определение производной и поясните ее физический смысл.
2.Точка движется по закону:
а) s(t) = t2
б) s(t) = 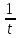
в) s(t) =t3
г) s(t) =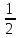 t + 1
t + 1
Укажите, какое из движений является равномерным, а какое равноускоренным
Найдите , по определению, производную функции f(х) = х2 – 4х
Как вы понимаете, что функция непрерывна в точке х0. Какая существует связь между непрерывностью функции в точке х0 и дифференцируемостью функции в этой точке.
Начертите схематически график функции, которая всюду непрерывна, но в точке х0 не имеет производной
Дифференцируемы ли следующие функции:
а) f(х) =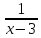 в точке х =3
в точке х =3
б) f(х) =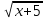 в точке х = -5
в точке х = -5
в) f(х) =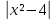 в точках х =-2, х = 2, х = 0
в точках х =-2, х = 2, х = 0
6. Напомнить основные свойства производной и правила нахождения производной сложной функции:
II
Задания вызванным ученикам.
В чем заключается геометрический смысл производной. Написать уравнение касательной.
Построить с исследованием график функции f(х) =
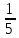 х2 -
х2 - 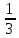 х3
х3
Заслушиваются ответы учеников
Устная работа класса
Касательная к графику функции f(х) =
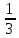 х3 – 2х2 + 3 параллельна оси абсцисс. Найдите абсциссы точек касания.
х3 – 2х2 + 3 параллельна оси абсцисс. Найдите абсциссы точек касания.Какой угол составляет с положительным направлением оси абсцисс касательная к графику функции f(х) =
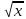 -
- 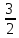 х + 3 в точке х0 = 1
х + 3 в точке х0 = 1Касательная к графику функции f(х) =3х2 -7 параллельна прямой у = 12х – 3. Найдите абсциссы точек касания.
Может ли касательная к графику функции:
- иметь более одной общей точки с графико м функции
- совпадать с графиком этой функции
5. Вопросы:
- верно ли, что если функция имеет производную в точке х0 , то она имеет и касательную в этой точке (да)
- Верно ли обратное утверждение (нет)
III
Задания вызванным ученикам.
- Дать геометрическую интерпритацию формулы Лагранжа;
- Найти координаты точки пересечения двух касательных к графику функции у= 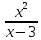 в точках с абсциссами х= 4 и х = -2.
в точках с абсциссами х= 4 и х = -2.
2. - Сформулировать достаточный признак возрастания ( убывания функции ) и доказать.
- Верно ли, что если функция возрастает на некотором промежутке, то ее производная положительна на этом промежутке.
- Найти наибольшее значение функции f(х) =- 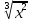 - х на промежутке
- х на промежутке 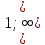 (-2)
(-2)
Устная работа класса
Какие из указанных функций убывают на множестве R :
f(х) =2х2 – 2х -3
f(х) = 4х -1
f(х) =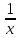
f(х) =-3х5
Начертите схематически график непрерывной функции, производная которой отрицательна на множестве R, за исключением двух точек, в которых производная равна нулю.
При каких значениях а функция f(х) =
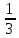 х3 + ах +3 возрастает на всей области определения (при а ≥0)
х3 + ах +3 возрастает на всей области определения (при а ≥0)
IV
Подведение итогов учителем по разобранному материалу:
Определение критических точек
Понятие о максимуме и минимуме функции
Теорема Ферма
Сформулировать достаточный признак экстремума
Верно ли, что если касательная к графику функции параллельна оси абсцисс в точках х1 и х2 , то х1 и х2 – точки экстремума.
V
Напоминание учителя о методах нахождения наибольшего и наименьшего значений функции на отрезке
Задания вызванным ученикам
- Найти наименьшее и наибольшее значения функции f(х) = х3 +х + 1 на отрезке 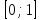
- Найти наибольшее значения функции f(х) =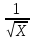 на промежутке
на промежутке 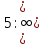
3. исследования функции с помощью производной дали следующие результаты

fᶦ + - +
-2 3
Как найти наибольшее значение функции на промежутке 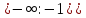 и ее наименьшее значение на отрезке
и ее наименьшее значение на отрезке 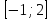 .
.
Итог урока
В заключении подводятся итоги урока и выставляются оценки учащимся, вызванным учителем, и тем, кто активно работал на уроке.
Если останется время, повторить методы построения графика функции с помощью производной.
Домашнее задание
Построить график функции f(х) = 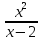 .
.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Урок-семинар по математике в 11 классе по теме: «Производная функции. Исследование функции с помощью производной» (20.23 KB)
Урок-семинар по математике в 11 классе по теме: «Производная функции. Исследование функции с помощью производной» (20.23 KB)
 0
0 700
700 26
26 Нравится
0
Нравится
0



