Получите свидетельство
Вход
1. Организационный момент
Здравствуйте, ребята! Рада Вас видеть! (Отметить отсутствующих)
Всё наше достоинство заключено в мысли, - писал французский математик и философ XVII века БлезПаскаль. Не пространство, не время, которых мы не можем заполнить, возвышает нас, а именно она, наша мысль. Будем же учиться правильно мыслить, изучая логику.
Сегодня мы продолжаем изучать тему «Логика». Запишите число, тему урока.
2. Постановка проблемы
Самым первым заданием я предлагаю вам заполнить бланки, лежащие у вас на партах.
(Приложение 1)
Я буду зачитывать утверждения. Вы должны поставить знак «+», если считаете, что утверждение верное, и знак «-», если считаете, что утверждение неверное.
| Любое логическое выражение либо истинно, либо ложно. |
| Сложное логическое выражение содержит высказывания, объединенные какой-то одной логической операцией. |
| Истинность сложного высказывания можно определить, зная истинность или ложность входящих в него высказываний. |
| Результатом операции отрицания над высказыванием «Пушкин – не гениальный русский поэт» является высказывание «Пушкин – гениальный русский поэт». |
| Высказывание «4 – простое число» истинно. Высказывание «4 – не простое число» ложно. |
| Высказывание «Тигр – это полосатый зверь или домашнее животное», полученное при помощи логического сложения, истинно. |
| Высказывание «Январь – последний зимний месяц и в нем всегда 31 день», полученное при помощи логического умножения, истинно. |
| Высказывание «День сменяет ночь тогда и только тогда, когда солнце скрывается за горизонтом» получено при помощи операции логического равенства. |
| Высказывание «Если число Х делится на 3, то оно делится и на 9», образованное при помощи операции логического следования, является истинным. |
| Даны высказывания «Учитель должен быть умным» и «Учитель должен быть справедливым». Объединение этих высказываний при помощи логической операции конъюнкции означает, что учитель должен быть одновременно и умным, и справедливым. |
Скажите мне, пожалуйста, сложно ли вам было определять истинность высказываний? А какие высказывания Вам были представлены? Простые или составные?
Вот сегодня на уроке мы научимся определять истинность составных высказываний, содержащих логические операции.
3. Актуализация знаний
1.Сформулируйте определение логика как науки .
Ответ. Логика - наука о законах и формах абстрактного мышления.
2.Какой вид логику мы изучаем на урок информатики?
Ответ: Математическую логику.
Кто является основателем математической логики и каков его вклад?
Ответ: Джорж Буль – создал азбуку математической логики, законы и орфографию.
Основной формой мышления являются высказывания.
Сейчас на слайде (слайд 2) видите предложения. Вы должны ответить являются ли они высказываниями?
Задание №1. Какие предложения являются высказываниями? Определить их истинность.
Число 6 – четное. (Да)
Чему равно расстояние от Земли до Марса? (Нет)
Все роботы являются машинами. (Да)
У каждой лошади есть хвост. (Да)
Внимание! Посмотрите направо. (Нет)
Кто отсутствует? (Нет)
Есть кошки, которые дружат с собаками. (Да)
Х2=0. (Да)
Электрон- элементарная частица. (Да)
10.Не нарушайте правила дорожного движения! (Нет)
Задание №2. Молодцы! Теперь решим другое упражнение. Вам нужно определить тип высказывания:
По типу высказывания бывают : 1. Общие (все, всякий, каждый, ни один);2. Частные (некоторые, большинство и т.п)
3. Единичные (все остальные) (Слайд 3)
«Все рыбы умеют плавать». Общее
Некоторые медведи – бурые. Частное.
Буква А – гласная. Единичное.
Некоторые мой друзья собирают марки. Частное.
Многие растения обладают целебными свойствами. Частное
Мой кот страшный забияка. Единичное
Не все книги содержат полезную информацию. Частное
Все ананасы приятны на вкус. Общее
Тигр – хищное животное. Общее
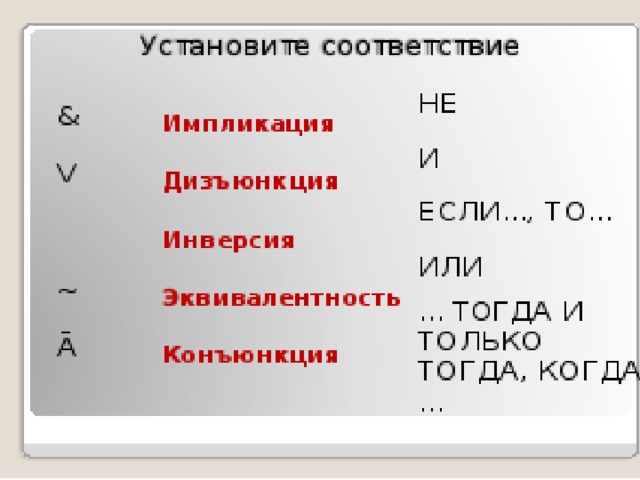
В математической логике не важен смысл высказывания, а важно только истинно оно или ложно. Поэтому простое высказывание обозначается латинской буквой. Сложное высказывание получается путем объединения простых высказываний союзами И, ИЛИ , НЕ , ЕСЛИ …., ТО…., ТОГДА И ТОЛЬКО ТОГДА, КОГДА. Перед вам логические операции. Необходимо установить соответствие между логическими операциями, их логическим обозначением и союзам или частицами.
Задание №3. (Слайд 4)
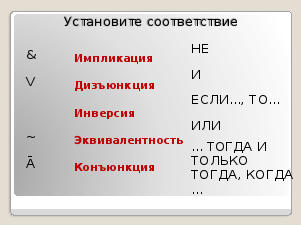
Теперь нам известно, что для построения сложного логического высказывания мы используем операции:
1. Инверсия
2.Конъюнкция.
3.Дизъюнкция.
4. Импликация (следование).
5.Эквивалентность.
Теперь составьте и запишите сложные высказывания из простых используя логические операции.
Запись логических выражений будем выполнять на доске и в тетради. Открыли тетради записали число.
Упр. №
Задание №4 (Слайд 5 и 6)
1.Часть туристов любят чай . Остальные туристы любят молоко. (А V В)
2. В кабинете есть учебники . В кабинете есть справочники. (А И В )
3. Любое из чисел X,Y,Z отрицательно. (ответ: ¬X V ¬Y V ¬Z.)
Теперь мы знаем как составлять сложные выражения. Рассмотрим различные виды записи лог. выражений.
Задание №5
На доске записано логическое выражение: F = X + Y * ¬Z
Записать данное выражение с помощью:
1.Союзов.
Ответ:F = X ИЛИ Y И (НЕ Z).
2.Операций используемых в программировании.
Ответ. F = X OR Y AND (NOT Z)
Задание №6. Найти значение данного выражения при значениях переменных Х=1;У=1; Z=0.
Для нахождения значения функции необходимо подставить значении переменных в формулу.
Ответ: F=1+1*( не 0)= 1+1*1=1.
Это единственное значение, которое может принять наша функция. (Нет).
От чего зависит значения функции? (От значений переменных X,Y, Z)
Из ранее изученного, нам известно, что для находили значение функции логической операции: инверсия, конъюнкция, дизъюнкция, инверсия, эквивалентность мы использовали таблицу Следовательно, тема нашего урока:
«ПОСТРОЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ ДЛЯ СЛОЖНОГО ЛОГИЧЕСКОГО ВЫРАЖЕНИЯ»
Запишем тему урока в тетрадь .
III. Объяснение нового материала.
Рассмотрим алгоритм построения таблицы истинности.
Давайте запишем определение таблицы истинности.
Чтобы построить такую таблицу, мы должны знать, сколько существует комбинаций всех возможных значений логических переменных. Для этого мы воспользуемся формулой:
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
Задание № 1. Построить (задача из учебника) стр. 172
Задача 2. Определить истинность следующего высказывания: «За окном светит солнце, и нет дождя».
Решение:
Нам дано сложное составное высказывание. Выделим из него простые высказывания:
А = «За окном светит солнце»
В = «За окном дождь»
Составим логическую функцию, соответствующую данному высказыванию.
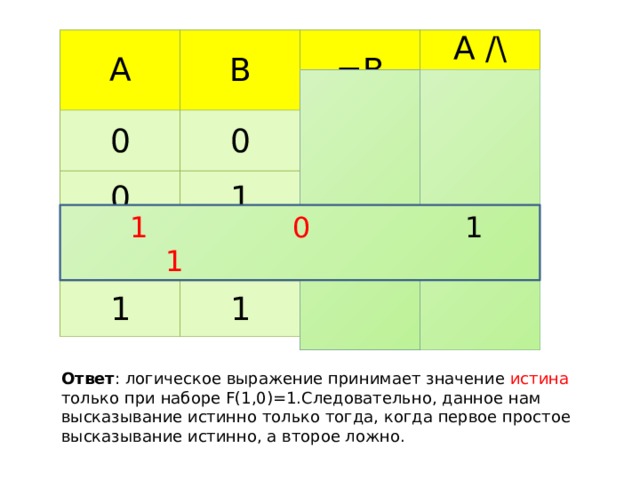
F(A, B) = A /\ ¬B
построим таблицу истинности для данной логической функции.
Ответ: логическое выражение принимает значение истина только при наборе F(1,0)=1.Следовательно, данное нам высказывание истинно только тогда, когда первое простое высказывание истинно, а второе ложно.
Задача 3. Определить истинность следующего высказывания: «Гости смеялись, шутили и не расходились по домам».
Решение:
Выделим из данного сложного высказывания простые высказывания:
А = «Гости смеялись»
В = «Гости шутили»
С = «Гости расходились по домам»
Составим логическую функцию, соответствующую данному высказыванию.
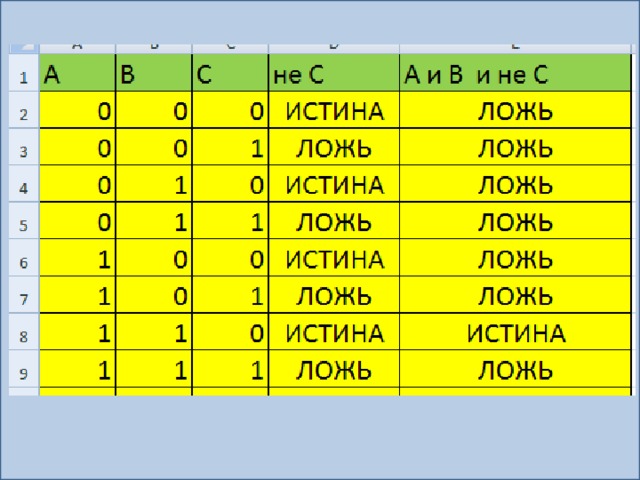
F(A, B, С) = A /\ B /\¬C
Построим таблицу истинности для данной логической функции.
Ответ: логическое выражение принимает значение истина только при наборе F(1,1,0)=1.Следовательно, данное нам высказывание истинно только тогда, когда первое и второе простые высказывания истинны, а второе ложно.
Вывод: Реальную задачу мы получаем в виде текста на естественном языке и, прежде чем приступить к ее решению, необходимо выделить простые высказывания, отношения между ними и перевести на язык формул (формализовать условие задачи, определяющее форму словесного высказывания).
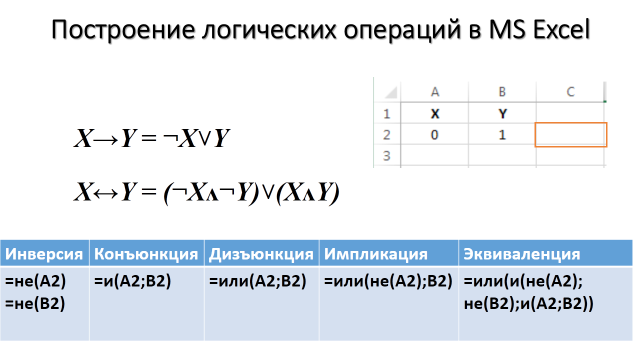
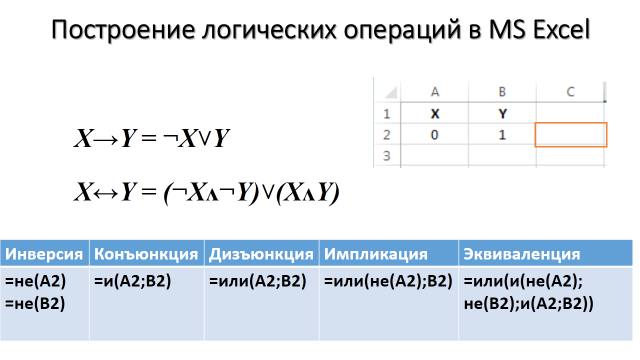
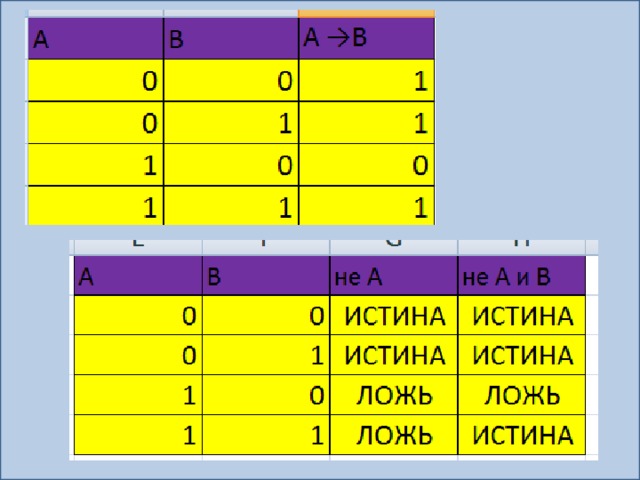
У вас должны получиться следующие таблицы истинности:
С помощью таблиц истинности докажите равносильность выражений 
Можно записать: 
в) Проверка правильности построения таблиц истинности
Садитесь за парты. Давайте проверим, правильно ли вы построили таблицы.
5. Закрепление
А если в выражении используются несколько логических операций? В каком порядке производить вычисления? Вспомним приоритет выполнения операций:
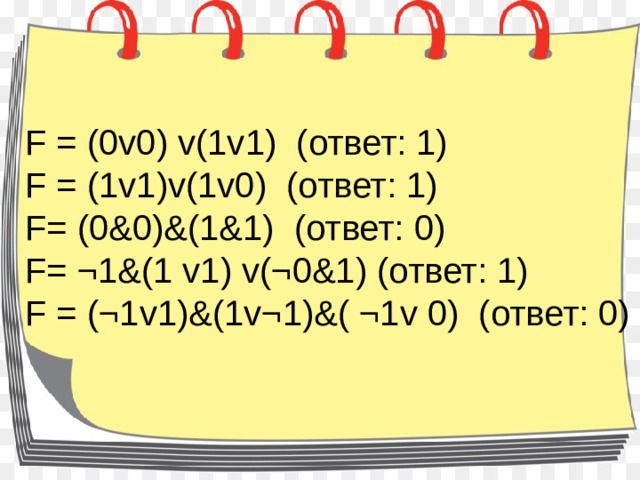
А теперь найдем значения логических выражений:
F = (0v0) v(lvl) (ответ: 1)
F = (lvl)v(lv0) (ответ: 1)
F= (0&0)&(1&1) (ответ: 0)
F= ¬1&(1 v1) v(¬0&1) (ответ: 1)
F = (¬1v1)&(1v¬1)&( ¬1v 0) (ответ: 0)
6. Рефлексия
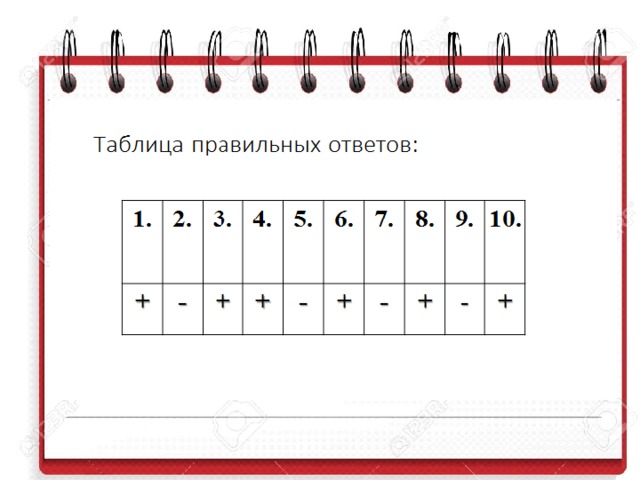
Теперь вернемся к самому первому заданию на уроке и попробуем его выполнить, зная таблицы истинности логических операций.
Проверьте себя и поставьте себе оценки.
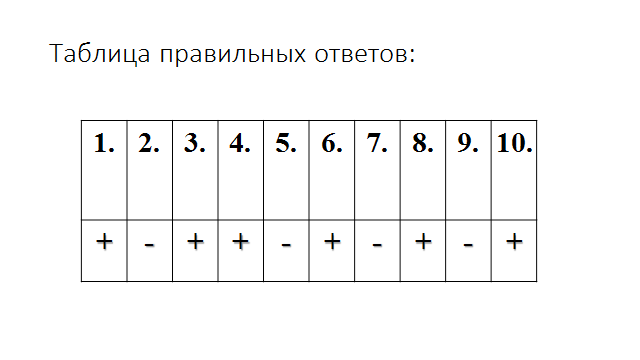
Если вы не допустили ни одной ошибки или исправили их до вывода правильных ответов – поставьте себе 5, если у вас 1-2 ошибки – поставьте 4, если 3 и больше поставьте 3.
Подведем итог нашего урока:
Что узнали нового? Что понравилось? Что вызвало затруднения?
Те, кому было очень интересно и те, кто разобрался в сегодняшней теме, поставьте себе в тетрадях улыбающийся смайлик. Те, кто считает, что ему нужно поработать над этой темой, поставьте подмигивающий смайлик. А те, кому было совершенно неинтересно и скучно, и те, совершенно ничего не понял, - грустный смайлик.
7. Домашнее задание
Возьмите карточки с домашним заданием.
Спасибо за урок, ребята
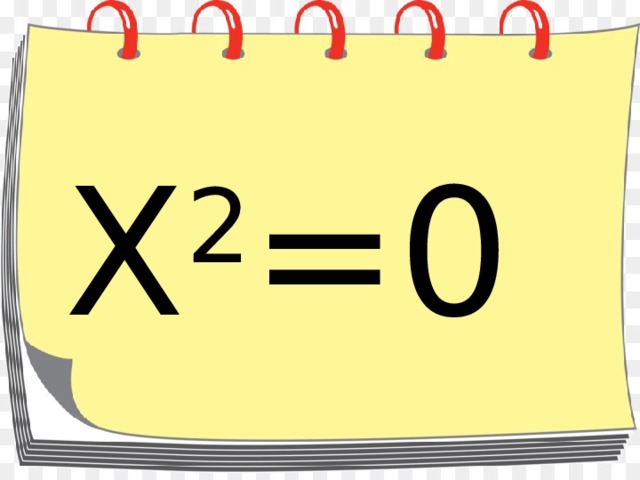
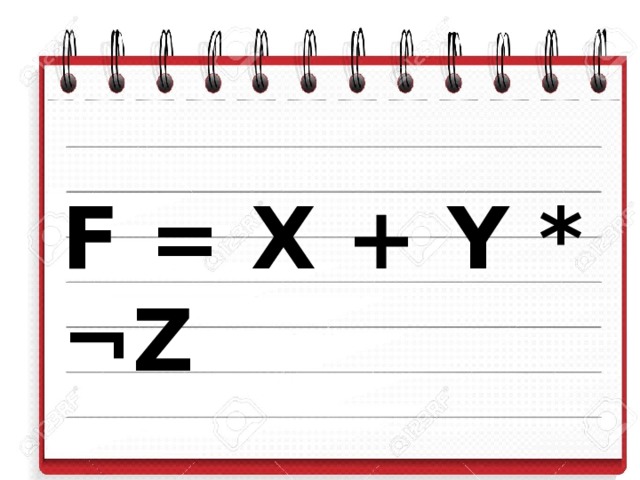
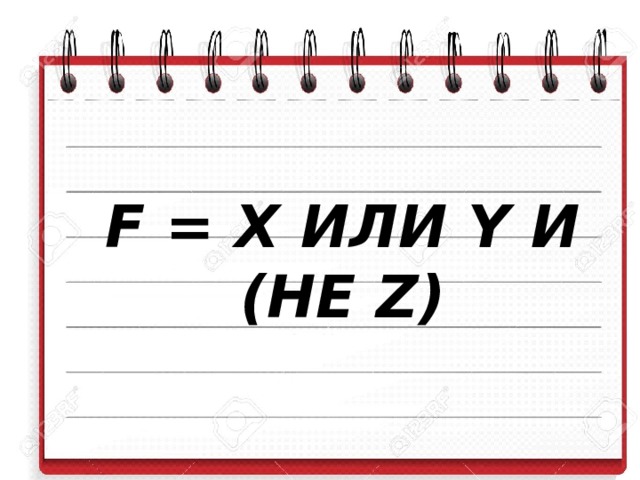
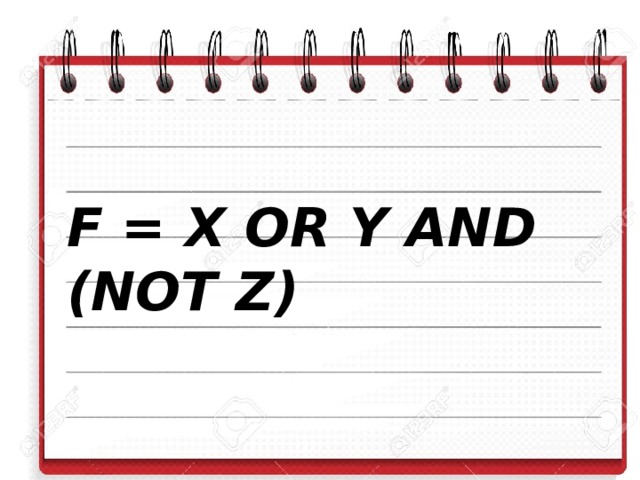
Урок по теме логика"Построение таблиц истинности сложного логического выражения" (2.8 MB)
0
869
57
Нравится
0
