Республика Бурятия
МО «Прибайкальский район»
МОУ «Таловская средняя общеобразовательная школа»
671253 Прибайкальский р-н, ст.Таловка
Телефон (830144) 59-1-04; 59-2-37; факс 59-1-04; e-mail talsosh2011@yandex.ru
ОТКРЫТЫЙ УРОК ПО МАТЕМАТИКЕ
9 КЛАСС
«АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ»
УЧИТЕЛЬ МАТЕМАТИКИ: НОВОСЕЛЬЦЕВА ЛЮДМИЛА ЕВГЕНЬЕВНА
МОУ «ТАЛОВСКАЯ СОШ», БУРЯТИЯ, ПРИБАЙКАЛЬСКИЙ РАЙОН, СТ. ТАЛОВКА
Тема урока: «Арифметическая прогрессия»
Тип урока: Урок изучения нового материала.
Цель урока: Формирование понятие арифметической прогрессии, формулы n-го члена, свойства членов арифметической прогрессии. Решение занимательных задач.
Задачи урока:
Образовательные – ввести понятия арифметической прогрессии; формулы n-го члена; характеристическое свойство, которым обладают члены прогрессий.
Развивающие – вырабатывать умения сравнивать математические понятия, находить сходства и различия, умения наблюдать, подмечать закономерности, проводить рассуждения по аналогии; сформировать умение строить и интерпретировать математическую модель некоторой реальной ситуации.
Воспитательные – содействовать воспитанию интереса к математике и ее приложениям, активности, умению общаться, аргументировано отстаивать свои взгляды.
Оборудование: презентация (Приложение 1)
Раздаточный материал: бумажные копии лекции, листочки с цифрами.
План урока:
Организационный момент
Устный счет
Изучение нового материала
Физминутка
Психологическая разгрузка
Подведение итогов урока
Рефлексия результативности
Домашнее задание
Ход урока
Организация начала урока
Учитель: «Здравствуйте, ребята! Сегодняшний урок я начну словами великого русского классика.
«О, сколько нам открытий чудных …
Готовит просвещенья дух,
И опыт – сын ошибок трудных,
И гений – парадоксов друг»
А.С. Пушкин
На сегодняшнем уроке мы продолжим изучать Числовые последовательности и Вы сможете самостоятельно сделать по-настоящему чудные открытия в данной области.
Устный счет
Скажите, где в повседневной жизни можно встретить числовые последовательности?
(Предполагаемые ответы: номера банковских счетов, домов на улице)
То есть числовой последовательностью можно назвать все те элементы природы, которые можно пронумеровать.
Перед Вами слайд.
Чему равен третий член первой последовательности? Последующий член? Предыдущий член?
Чему равна разность между вторым и первым членами? Третьим и вторым членами? Четвертым и третьим?
Сделайте вывод, какой будет разность между десятым и девятым членами первой последовательности?
Назовите два последующих члена последовательностей. Почему Вы так считаете?
(Ответы учеников)
Объедините некоторые последовательности по общему свойству. Сформулируйте это свойство.
(Предполагаемые ответы: первая, третья и четвертая последовательности обладают общим свойством. Каждый последующий член последовательности равен предыдущему, сложенному с одним и тем же числом. Это последовательности №1,3,4)
Числовые последовательности, обладающие этим свойством, называются Арифметическими прогрессиями. Дайте определение арифметической прогрессии.
(Ответы учеников)
Изучение нового материала
| Это тема сегодняшнего урока. На этом уроке мы узнаем ЧТО такое арифметическая прогрессия, ОТКУДА она возникла, КАКОЙ общий вид она имеет, и решим задачи ГДЕ они используются? Возьмите на краю стола напечатанные лекции (Приложение 2) и цветные карандаши (фломастеры). Выделяйте и вписывайте основные понятия и формулы по данной теме в лекциях. |
|
Определение арифметической прогрессии.
Основные определения и данные для арифметической прогрессии сведенные в одну таблицу:
| Определение арифметической прогрессии | Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом. |
| Разность арифметической прогрессии | Равна разности последующего и предыдущего члена прогрессии |
| Арифметическая прогрессия является возрастающей | Если разность арифметической прогрессии больше нуля |
| Арифметическая прогрессия является убывающей | Если разность арифметической прогрессии меньше нуля |
| Формула n-го члена арифметической прогрессии |
|
| Характеристическое свойство прогрессии | |
(Ответы учеников, учитель записывает их на доске
Арифметическая прогрессия: 4, 3, 2, 1, 0, -1. Чем отличается эта прогрессия от рассмотренных?
Она убывающая, потому разность в ней отрицательна.
(Ответ: Она убывающая)
А чему равна разность этой прогрессии?
(Ответ: разность отрицательна и равна (-1)
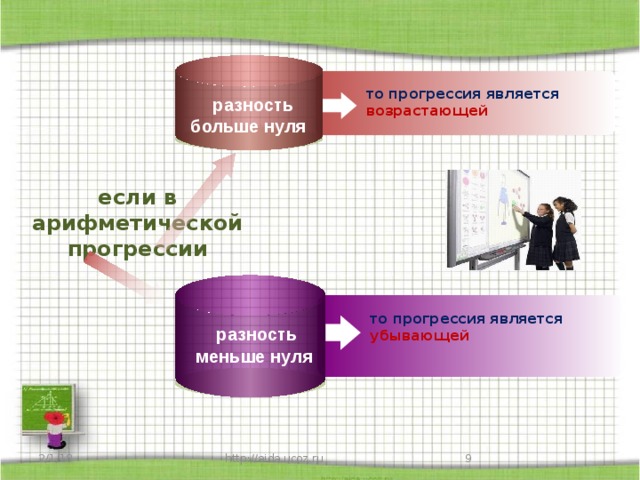
Итак, Если в арифметической прогрессии разность больше нуля, то прогрессия является возрастающей
Если в арифметической прогрессии разность меньше нуля, то прогрессия является убывающей
Впишите в свои конспекты, термины возрастающей и убывающей арифметической прогрессий.
Так как арифметические прогрессии – это разновидность числовых последовательностей, то все свойства последовательностей могут быть перенесены и на арифметические прогрессии. Какие свойства числовых последовательностей Вы знаете?
(Ответы учеников – конечность и бесконечность, монотонность)
Рассмотрим второй вопрос темы – ОТКУДА возникли числовые последовательности?
Числовые последовательности настолько уникальны и интересны, что интересовали людей с древних времен. Об этом свидетельствую огромное количество задач, дошедших до наших дней. Перед вами часть папируса Ахмеса (записан ок. 1650 года до н. э.); это первый источник древности, в котором описаны задачи на арифметические прогрессии. Задачи в нем имеют прикладной характер и связаны с практикой строительства, размежеванием земельных наделов и т. п. Слово прогрессия латинского происхождения и означает «движение вперед».
КАКОВ вид общего члена у арифметической прогрессии?
Как задать арифметическую прогрессию?
Достаточно задать ее первый член и разность.
И все последующие члены уже можно найти следующим образом – второй член равен первый член плюс разность, третий равен второй член плюс разность. А если надо найти - чему равен сто одиннадцатый член прогрессии, неужели придется искать все предыдущие члены?
Нет, ребята. «Дорогу осилит идущий, а математику – мыслящий». Так давайте же поразмыслим, как можно вывести общую формулу арифметической прогрессии.
(Наводящие вопросы: Чему равен второй член прогрессии? Чему равен третий член прогрессии? А если теперь вместо второго подставить первый плюс разность? Выведите общее свойство для
n-ного члена прогрессии.)
(Учащиеся приходят к выводу общей формулы n-ного члена арифметической прогрессии.)
Выделите и допишите формулу в своих конспектах.
Решим задачу, предложенную на слайде.
(К доске выходит учащийся, а остальные записывают ее в тетрадь.)
Обратите внимание на арифметическую прогрессию. 3, 7, 11, 15, 19, 23. Чему равен четвертый член этой прогрессии? (15) А чему равен предыдущий и последующий члены? (11 и 19) Выразите третий член через его последующий и предыдущий члены?
(Ответы учеников: (11+19)/2)
Рассмотрите пятый член, и попробуйте выразить его через предыдущий и последующий. Найдите аналогию. Сформулировать свойство.
(Предполагаемые ответы: каждый член прогрессии равен среднему арифметическому между предыдущим и последующим членами)
Это свойство называется характеристическим свойством арифметической прогрессии.
Если для каждого члена последовательности, начиная со второго, выполняется следующее условие, то эта последовательность будет являться арифметической прогрессией. Выделите это в своих конспектах.
Пользуясь этим свойством определите, какие из данных последовательностей являются арифметическими прогрессиями и определите разность этих прогрессий.
А сейчас давайте разберем ГДЕ используется арифметическая прогрессия. Решим задачу.
Задача. Найти количество всех трехзначных натуральных чисел, делящихся на 7.
Решение. Наименьшее трехзначное число, делящееся на 7 без остатка, есть 105, а наибольшее число – 994.
Задача. В арифметической прогрессии найти a10, если a25 − a20 = 10, и a16 = 13.
Психологическая разгрузка
| У Вас на столах лежат листы, на которых написаны цифры от 1 до 9. Теперь раскрасьте один ряд двумя разными цветами в любом порядке. Как я это сделала, показано на слайде. А пока Вы раскрашиваете, я расскажу про замечательного математика по фамилии Рамсей. Он жил в начале ХХ века. Им была создана теория, доказывающая, что в мире нет абсолютного хаоса. Что даже, казалось бы, самая неупорядоченная система имеет определенные математические закономерности. Вспомните, когда Вы смотрите на звезды, то может показаться, что расположены они в самом случайном порядке. Но еще в древности люди увидели там созвездия Рыб и Касеопеи, Льва и Ориона. И вот на ваших карточках казалось бы цифры раскрашены в случайном порядке. Но Рамсей доказал, что это не так, доказав следующий факт: Обратите внимание, что хотя бы три каких – либо числа одного цвета обязательно составляют арифметическую прогрессии. Запишите эти числа. |
|
Подведение итогов урока
И вспомним начало нашего урока, ребята. Удалось ли за сегодняшний урок сделать чудные открытия?
А какие открытия Вы для себя сделали?
(Предполагаемые ответы: Мы узнали что такое арифметическая прогрессия, как находится ее n-ный член, и историю появления прогрессий и т.п.)
А какие цели урока мы ставили перед собой?
Как Вы считаете, нам удалось достигнуть поставленных целей?
Спасибо за урок, ребята. Мне кажется, что Вы сегодня хорошо потрудились.
Рефлексия результативности
Ребята, а теперь сами оцените свою работу на уроке. Перед вами карточка с изображением горы. Если вы считаете, что хорошо усвоили на уроке, разобрались в понятии арифметической прогрессии, то нарисуйте себя на вершине горы. Если осталось что-то неясно, нарисуйте себя ниже, а слева или справа решите сами.
Передайте мне свои рисунки
Домашнее задание
Вашим домашним заданием будут четыре задачи ваших конспектов. Надеюсь, что у большинства решение задач не вызовет затруднений.
Подсказка в лекциях и в учебнике
| Определение арифметической прогрессии |
|
| Разность арифметической прогрессии |
|
| Арифметическая прогрессия является возрастающей |
|
| Арифметическая прогрессия является убывающей |
|
| Формула n-го члена арифметической прогрессии |
|
| Характеристическое свойство прогрессии | |
| Характеристическое свойство арифметической прогрессии | |
| Определение арифметической прогрессии |
| |
| Разность арифметической прогрессии |
| |
| Арифметическая прогрессия является возрастающей |
| |
| Арифметическая прогрессия является убывающей |
| |
| Формула n-го члена арифметической прогрессии |
| |
| Характеристическое свойство прогрессии | | |
| Характеристическое свойство арифметической прогрессии | | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |










| a1 | d | an | n |
| 10 | 4 |
| 5 |
| 5 | 2 | 19 |
|
| 2 |
| 156 | 12 |
| – 35 | 5 |
|
|
| d | an | n | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 4 | | 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 2 | 19 | | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | | 156 | 12 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| – 35 | 5 | | | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a1 | d | an | n |
| 10 | 4 |
| 5 |
| 5 | 2 | 19 |
|
| 2 |
| 156 | 12 |
| – 35 | 5 |
|
|
| a1 | d | an | n |
| 10 | 4 |
| 5 |
| 5 | 2 | 19 |
|
| 2 |
| 156 | 12 |
| – 35 | 5 |
|
|
| a1 | d | an | n |
| 10 | 4 |
| 5 |
| 5 | 2 | 19 |
|
| 2 |
| 156 | 12 |
| – 35 | 5 |
|
|
| a1 | d | an | n |
| 10 | 4 |
| 5 |
| 5 | 2 | 19 |
|
| 2 |
| 156 | 12 |
| – 35 | 5 |
|
|

 Получите свидетельство
Получите свидетельство Вход
Вход





























 Урок по теме "Арифметическая прогрессия" (909.25 KB)
Урок по теме "Арифметическая прогрессия" (909.25 KB)
 0
0 1554
1554 144
144 Нравится
0
Нравится
0


