Получите свидетельство
Вход
Классная работа 08.10.21.
Метод интервалов
Рассмотрим функцию:
Отсюда ясно, что :
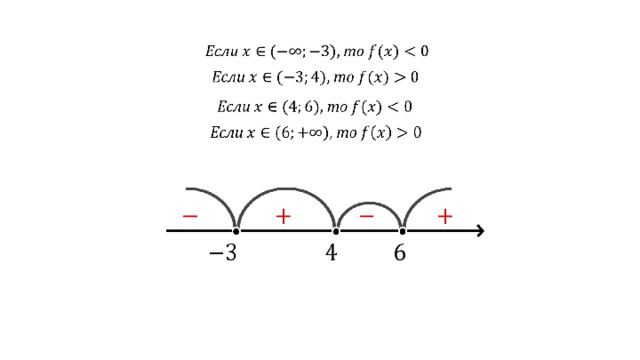
Пусть функция задана формулой:
В каждом из промежутков, на которые область определения
разбивается нулями функции, знак функции сохраняется,
а при переходе через нуль ее знак изменяется.
В каждом из промежутков, на которые область определения
разбивается нулями функции, знак функции сохраняется,
а при переходе через нуль ее знак изменяется.
Пример 1
Решим неравенство :
Решим неравенство:
Пример 2
Решим неравенство:
Решим неравенство:
Пример 3
Решим неравенство:
Пример 4
Решим неравенство:
![Пример 5 Решим неравенство: Ответ: (2; 6]](https://fsd.videouroki.net/html/2021/10/22/v_61720fefe7938/img12.jpg)
Пример 5
Решим неравенство:
Ответ: (2; 6]
Урок по алгебре 9 класс "Метод интервалов" С.М. Никольский (1.1 MB)
0
239
72
Нравится
0
