Учитель математики
высшей квалификационной категории
МОУ «Гимназия «19»
г.Саранск Республика Мордовия
Наумова Тамара Владимировна
Урок математики (5 класс)
«В мире геометрических фигур»
Цели урока:
Образовательные:
- повторить, закрепить и расширить начальные геометрические знания учащихся;
- проверить усвоение учащимися умения решать геометрические задачи с помощью уравнений.
Воспитательные:
- прививать интерес к изучению математики;
- воспитывать эстетический вкус, чувство коллективизма.
Развивающие:
- расширить кругозор учащихся, умение работать по заданному алгоритму;
- развивать моторику рук, ориентировку на плоскости и в пространстве, внимание.
Тип урока: комбинированный.
Оборудование:
Листы с печатной основой.
Доска с заранее подготовленным чертежом.
Модели различных многоугольников.
Схемы построения фигуры.
Различные фигурки, собранные способом оригами;
Чертежные инструменты.
Ход урока:
I. Организационный момент.
Добрый день, ребята, уважаемые гости!
Приятно видеть вас сегодня такими праздничными, ведь наш урок необычен, он проходит в рамках дней наук и посвящается математике. А правильнее будет сказать, одной из её частей – геометрии. Геометрия самая древняя наука. Даже термин математика возник гораздо позднее, чем геометрия. Ученые древности и средневековья, занимавшиеся в нашем понимании математикой, называли себя геометрами. Некоторые утверждения геометрии относят к древнейшим памятникам мировой культуры, которые старше самой известной в мире книге Библии.
Можно сказать, что геометрия, это не совсем та математика, с которой мы привыкли иметь дело. Геометрия – это предмет для тех, кому нравиться фантазировать, рисовать, рассматривать картинки, кто умеет наблюдать, замечать и делать выводы.
Один мудрец сказал: «Высшее проявление духа – это разум. Высшее проявление разума – это геометрия. Клетка геометрии – треугольник. Он так же неисчерпаем, как и Вселенная».
Сегодняшний урок мы посвящаем треугольнику, но не забудем и о геометрических фигурах, вспомним, что знаем о них, проверим свои знания, выполняя самостоятельные работы, закрепим свои знания в ходе необычной практической работы.
Работать на уроке будем, сочетая устную и письменную работы, индивидуальную и коллективную.
Будьте активными, чтобы в конце урока сделать себе подарки не только в виде новых знаний, но и высоких оценок!
II. Повторение изученного материала
- Начнём с повторения, какие фигуры изображены на рисунках? (Демонстрируются рисунки с лучом, отрезком, точкой, отрезком, треугольником, о котором говорится более подробно).
- Вспомним, глядя на плакат, из каких элементов состоит треугольник?
B
A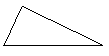 C
C
3 вершины (точки А, В, С)
3 стороны (отрезки АВ, ВС, АС)
3 угла (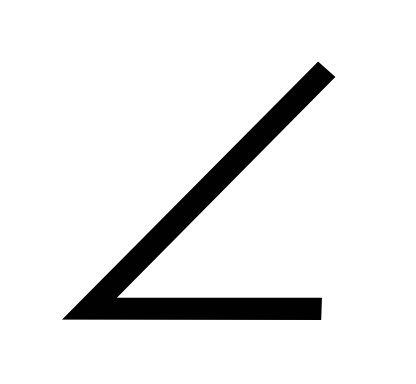 А,
А, 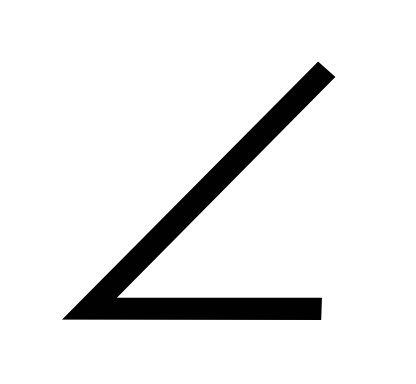 В,
В, 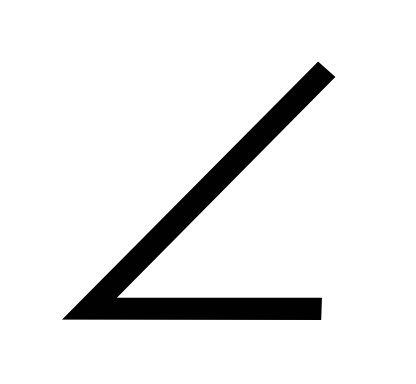 С)
С)
- Продолжите фразу:
- cторона АВ противолежит 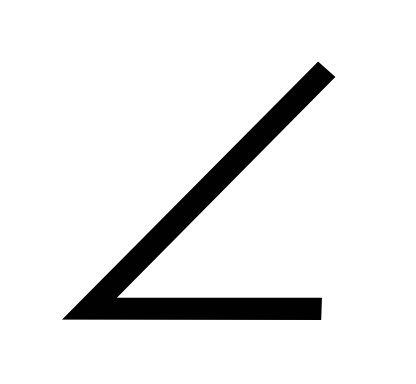 _____
_____
- 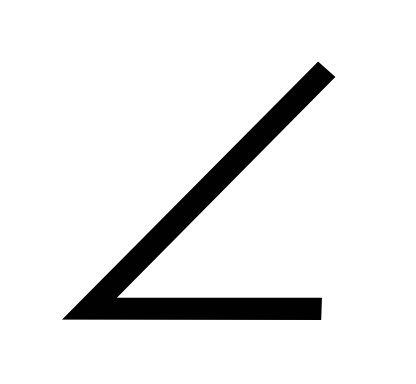 В противолежит стороне _____
В противолежит стороне _____
- С прилежит к сторонам _____
Треугольник иногда ещё называют «королём» геометрии. А королям посвящают оды и стихи. Послушаем одно из них (читает ученик, демонстрирует реечные модели).
Знает, братцы, каждый школьник
Про фигуру «Треугольник»,
Знает с ранних лет.
В геометрии обычной
Много есть фигур отличных,
А подобных нет!
Пусть фигура я простая,
Но конструкция такая
Стоит громких слов.
У меня характер твёрдый,
И держу я форму гордо
У своих углов.
Да, я жёсткая фигура,
Моя крепкая натура
Слабым - не родня.
И наука не молчала:
Все евклидовы «Начала»
Начались с меня.
Я всегда живу без скуки,
Со мной связано в науке
Множество имён:
Пифагор меня прославил,
Про меня задачи ставил сам Наполеон!
Учитель: В стихотворении прозвучало свойство жесткости треугольника. Часто ребята не воспринимают это свойство, а оно является основным для треугольника. Даже, если стержни, образующие треугольник, соединить шарнирно, то его невозможно изменить, в отличие от четырёхугольников и многоугольников с большим количеством сторон, где такое соединение допускает изменение формы многоугольника. За «жесткость» треугольник очень любят инженеры. Многие конструкции зданий, мостов состоят из треугольников.
III. Самостоятельная работа на заполнение пропусков.
Настало время проверить, как каждый из вас умеет работать с основными геометрическими фигурами. (Выполняется самостоятельная работа на листочках с печатной основой, время работы 5 мин).
IV. Повторение ранее изученного материала.
- Ребята, а каким способом мы научились решать задачи на последних уроках математики? (С помощью уравнений).
- Решением уравнений занимается сестра геометрии – алгебра, приступим к её изучению в 7-ом классе. Вспомним, какие задачи можно решать с помощью уравнений? (В которых есть несколько неизвестных величин и сказано, как они между собой связаны, а также есть условие, позволяющее составить равенство из этих величин, выраженных через Х).
- Перед выполнением второй самостоятельной работы устно решим следующую задачу: в треугольнике АВС сторона АС больше ВС на 8см, а сторона ВС меньше АВ на 10см. Найдите каждую сторону треугольника АВС, если его периметр равен 48 см. (Обсуждается ход решения, по ходу учитель заполняет рисунок на доске и записывает решение:
ВС=х см, АС=х+8 (см), АВ=х+10(см), Р=АВ+ВС+АС,
х+х+8+х+10=48,
3х + 18 =48,
3х=48-18,
3х=30,
х=30:3,
х=10.
ВС=10см, АВ=10+10=20(см), АС=10+8=18 (см).
- Как проверить, правильно ли решили задачу? (Сложить длины сторон, их сумма должна равняться 48 см).
V. Самостоятельная работа на листочках с печатной основой (5 мин)
- А сейчас каждый из вас решит подобную работу на листочках с печатной основой (в 2-ух вариантах), будьте внимательны, какую из сторон удобнее обозначить через х, решение краткое.
VI. Физкультминутка
- Много решали, умственно напрягались, пришло время для физкультминутки:
Раз, два – выше голова,
Три, четыре – плечи шире,
Пять, шесть – тихо сесть,
Семь, восемь – лень отбросим.
Практическая работа
- Продолжаем вспоминать, что знаем о геометрических фигурах. Часто встречались с квадратом, вспомним, что вы знаете о нем, его свойствах, опираясь на его бумажную модель.















Итак, квадрат обладает большим количеством свойств, все эти свойства в дальнейшем изучим подробнее и докажем их, а пока запомните, что все углы квадрата прямые и каждая диагональ квадрата делит его на два равных треугольника, называемых прямоугольными.
Следующий этап урок – практическая работа с элементами древней японской игры оригами, но, играя, мы будем учиться. Помните, как утверждают ученые: «Чем лучше работают руки, тем лучше думает голова».
- Возьмите модель треугольника на вашем столе. Разовьем вашу наблюдательность. Это треугольник получен из квадрата, значит какой у него есть угол? (Прямой).Запомните, что такой треугольник называется
прямоугольным. 
- А что можно сказать о сторонах угла, образующих прямой угол? (Они равны)
- А как это проверить, не имея под рукой масштабной линейки?
(Совместить стороны).
- Проверим это, действительно, они равны. Запомните, такой треугольник называют равнобедренным?
-Когда перегибали треугольник, что при этом получилось? (2 треугольника)
- Развернем его. Каждый полученный треугольник разделим еще на два равных треугольника, совмещая стороны острых углов с вершиной прямого угла. Зафиксируйте линии сгиба.
- Какую фигуру получили? (Квадрат). 
- Как называется отрезок, соединяющий две противоположные вершины? (Диагональ). У нас одна диагональ видна.
- Сколько всего диагоналей у квадрата? (Две).
- Работаем с моделью квадрата. Можно сказать, что у нас двойной квадрат. Один разбит на два равных треугольника, а другой нет. Переверните фигуры так, чтобы перед вами был сплошной квадрат и соединим нижнюю вершину с верхней. На какие фигуры разделился сплошной квадрат? Сделаем поворот модели на плоскости. У нас образовался кармашек.  Проверьте. Рассмотрим видимые прямоугольные треугольники нижнего квадрата. Вершины меньших прямоугольных треугольников заправим в кармашек.
Проверьте. Рассмотрим видимые прямоугольные треугольники нижнего квадрата. Вершины меньших прямоугольных треугольников заправим в кармашек.  Зафиксируем по одной линии.
Зафиксируем по одной линии.
- Сколько углов у полученной фигуры? (Пять).
- Обратимся к левой и правой вершинам исходного квадрата. Поместим их на линию кармашка.
- Какие при этом получились фигуры?  (снова треугольники). У нас есть еще прямые углы над линией кармашка. Вершины этих углов соединим с линией кармашка слева и справа.
(снова треугольники). У нас есть еще прямые углы над линией кармашка. Вершины этих углов соединим с линией кармашка слева и справа. 
- Итак, каждый раз перегибая треугольный лист бумаги, мы получали или треугольники или квадраты.
Зафиксируйте еще раз все линии сгиба и переверните фигуру. Что она вам напоминает?  (Сердце). А можно сказать, что это многоугольник и почему? (Да, состоит из непересекающихся отрезков и углов). Получили этот многоугольник методом оригами. О свойствах и видах многоугольников вы подробно узнаете в восьмом классе. А пока пусть эта фигура остается для вас сердцем, которое вы сделали кончиками своих пальцев, передавая ему частичку себя, своей души. Тем и уникально это древнее искусство. Из обыкновенного листа бумаги можно сделать множество полезных и забавных фигур.
(Сердце). А можно сказать, что это многоугольник и почему? (Да, состоит из непересекающихся отрезков и углов). Получили этот многоугольник методом оригами. О свойствах и видах многоугольников вы подробно узнаете в восьмом классе. А пока пусть эта фигура остается для вас сердцем, которое вы сделали кончиками своих пальцев, передавая ему частичку себя, своей души. Тем и уникально это древнее искусство. Из обыкновенного листа бумаги можно сделать множество полезных и забавных фигур.
Перед вами выставка работ, сделанных в этой технике вашими сверстниками прошлых лет, фигурки самые разные: и плоские и пространственные, но все они получались из квадратного листа бумаги. Хочу прочитать вам стихотворение, сочиненной моей бывшей ученицей:
Что такое оригами?
Задала вопрос я маме
И ответила она:
“Это целая страна!
Там чудесно оживают
Птицы, звери и цветы,
Там таинственно, как в сказке,
Все сбываются мечты”.
И тогда решила я -
Это чудо оригами
Буду я любить всегда.
V. Домашнее задание
Фигурки взять с собой, дома развернуть, снова собрать по имеющимся линиям и повторить алгоритм сборки данной фигуры на другой модели прямоугольного равнобедренного треугольника.
Подведение итогов и окончание урока
Наш урок подходит к концу. Давайте соединим наши руки со всеми бумажными сердечками воедино. Получим цепь наших сердец. Передадим через нее друг другу доброту, счастье, радость, успех, здоровье, все то, чем мы можем поделиться друг с другом, с нашими близкими и родными.
Спасибо за урок! Работали хорошо, особо хочу отметить … Оценки за этот урок узнаете после того, как я проверю ваши работы.
ПРИЛОЖЕНИЕ
СХЕМА ПОСТРОЕНИЯ ФИГУРЫ



Рис. 1 Рис. 2 Рис. 3



Рис.4 Рис.5 Рис. 6

 Получите свидетельство
Получите свидетельство Вход
Вход


 C
C 


















 Урок математики "В мире геометрических фигур" (66.5 КB)
Урок математики "В мире геометрических фигур" (66.5 КB)
 0
0 825
825 26
26 Нравится
0
Нравится
0









