Цели урока:
Обучающая – формирование у учащихся понимания вероятности, равновероятных событий, неравновероятных событий; вероятностного подхода к измерению информации;
Развивающая – развивать умение качественно оценивать поставленную задачу для правильного выбора способа решения задачи; развивать самостоятельность; логическое мышления учащихся.
Воспитательная – формировать интерес к предмету, навыки контроля и самоконтроля; чувство ответственности, деловые качества учащихся.
Оборудование: доска, маркер, карточки - памятки, справочный материал.
Тип урока: комбинированный: объяснение нового материала с выполнением практической работы.
Ход урока
I. Организационный момент.
II. Актуализация знаний.
Задача: Какое сообщение содержит большее количество информации?
В классе 32 ученика. Какое количество информации содержится в сообщении о том, что к доске пойдёт Коля Сидоров; (Отв. : 5 бит. )
Вася получил за экзамен оценку 4 (по 5 - бальной системе единицы не ставят). (Отв. : 2 бит. )
Сообщение о том, что из корзины с разноцветными шарами (все шары разного цвета) достали зелёный шар, содержит 4 бита информации. Сколько шаров было в корзине? (Отв. : 2 бит. )
В классе 30 человек. За контрольную работу по информатике получено 15 пятерок, 6 четверок, 8 троек и 1 двойка. Какое количество информации несет сообщение о том, что Андреев получил пятерку? Какое количество информации несет сообщение о том, что Андреев получил любую оценку?
Первые три варианта учащиеся решают без затруднения. События равновероятны, поэтому можно применить для решения формулу Хартли. Но третье задание вызывает затруднение. Делаются различные предположения. Роль учителя: подвести учащихся к осмыслению, что в четвертом варианте мы сталкиваемся с ситуацией, когда события неравновероятны. Не все ситуации имеют одинаковые вероятности реализации. Существует много таких ситуаций, у которых вероятности реализации различаются.
Сегодня на уроке мы должны ответить на вопрос: как вычислить количество информации в сообщении о неравновероятном событии.
III. Изучение нового материала.
Для вычисления количества информации в сообщении о неравновероятном событии используют следующую формулу: I=log2(1/p), заметим, что ранее мы использовали формулу Хартли следующего вида I=log2(N), на самом деле эти формулы не разные! Формула Хартли является частным случаем второй , для случая, когда вероятность исходов события оказывается одинаковой (в случае, например, если бы мы кидали монету и вероятность выпадет орел или решка была бы равновероятна).
Теперь вернемся к нашей формуле и разберем ее более подробно.
I – это количество информации, р – вероятность события.
Вероятность события выражается в долях единицы и вычисляется по формуле: р=K/N,
где К – величина, показывающая сколько раз произошло интересующее нас событие, N – общее число возможных исходов какого - то процесса.
Вернемся к нашей задаче.
Пусть К5 – это количество пятерок, К5=15
К4 – количество четверок, К4=6
К3 – количество троек, К3=8
К2 – количество двоек, К2=1
N – общее количество оценок, N = К5 +К4 + К3 +К2=15+6+8+1=30
Вычислим вероятность, что Андреев получил пятерку, которое при этом было получено.
Вероятность, что Андреев получил пятерку: р5=15/30=1/2=0, 5.
Вероятность, что Андреев получил четверку: р4=6/30=1/5=0, 2.
Вероятность, что Андреев получил тройку: р3=8/30=4/15=0, 27.
Вероятность, что Андреев получил четверку: р4=1/30=0, 03.
Обращаем внимание учащихся на то, что в сумме все вероятности дают 1.
Вычислим количество информации, содержащееся в сообщении, что Андреев получил пятерку: I5=log2(1/p5)= log2(1/0, 5)=log22=1 бит.
Затем, ученикам предлагается вычислить количество информации остальных оценок.
Вычислим количество информации, содержащееся в сообщении, что Андреев получил четверку: I4=log2(1/p4)= log2(1/0, 2)= log25=2, 32 бит.
Вычислим количество информации, содержащееся в сообщении, что Андреев получил тройку: I3=log2(1/p3)= log2(1/0, 27)= log23, 7=1, 9 бит.
Вычислим количество информации, содержащееся в сообщении, что Андреев получил двойку: I2=log2(1/p2)= log2(1/0, 03)= log233, 3=4, 9 бит.
Пояснение: если учащиеся не умеют вычислять значение логарифмической функции, то можно использовать при решении задач этого урока следующие приемы:
Ответы давать примерные, задавая ученикам следующий вопрос: «В какую степень необходимо возвести число 2, чтобы получилось число, стоящее под знаком логарифма?».
Применить таблицу из задачника - практикума под редакцией Семакина И. Г. и др.
При сравнении результатов вычислений получается следующая ситуация: чем меньше вероятность события, тем больше информации несет сообщение о нем, то есть вероятность получения двойки была самая маленькая, но при этом информационный объем по сравнению с другими самый большой. Это не случайность, а закономерность. Приведем еще примеры об исходах события с разной вероятностью и сравним их информативность. Вот, скажем сообщение об осадках в зимнем прогнозе погоды. Зимой бывает снег, бывает отсутствие осадков и, очень редко, бывает дождь (во время сильной оттепели). Дождь зимой маловероятен, поэтому зимой сообщение о дожде несет самую большую информацию.
Качественную связь между вероятностью события и количеством информации в сообщении об этом событии можно выразить так: чем меньше вероятность некоторого события, тем больше информации содержит сообщение об этом событии.
Вернемся к нашей задаче об оценках Андреева. Попробуем ответить на вопрос: сколько получим информации при получении любой оценки?
Ответить на этот вопрос нам поможет формула вычисления количества информации для событий с различными вероятностями, которую предложил в 1948 г. американский инженер и математик К. Шеннон.
Весь материал – смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход




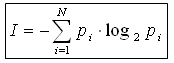

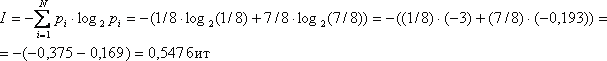









 Урок информатики "Измерение информации. Вероятностный подход" (0.19 MB)
Урок информатики "Измерение информации. Вероятностный подход" (0.19 MB)
 0
0 3323
3323 797
797 Нравится
1
Нравится
1


