Муниципальное бюджетное общеобразовательное учреждение
Средняя общеобразовательная школа № 4 имени П. И. Климука
Щёлковского муниципального района Московской области
Открытый урок - путешествие
«Математическое путешествие по стране Обыкновенная дробь»
5 класс
учитель математики
Корунова Н.В.
Математическое путешествие
по стране «Обыкновенная дробь».
Цели урока:
1) Обобщение и систематизация знаний, умений, навыков учащихся по пройденной теме «Обыкновенные дроби» по учебнику И.И. Зубаревой, 5 класс.
2). Развитие памяти, внимания, математической речи, логического мышления и самостоятельности.
3). Выработка интереса к предмету, воспитание чувства ответственности за коллектив, коммуникативных навыков.
Форма урока: игровая, урок – путешествие.
Здравствуйте, ребята. Садитесь.
Как вы думаете, ребята, зачем надо изучать математику? Ответ на этот вопрос вы найдёте, если узнаете, что означает, в переводе с греческого слово «математика».
«Математика» - знание, наука. Именно поэтому, с давних времён, считали, если человек был сведущ в математике, то это всегда означало высшую степень учёности.
Хочется, чтобы сегодня все ученики вашего класса показали, насколько они мудры, и на сколько сведущие люди в математике 5 класса.
Сегодня на уроке мы поговорим с вами об «Обыкновенных дробях» и обобщим знания по этой теме полученные на предыдущих уроках.
Урок будет необычный, мы отправимся с вами в путешествие по стране «Обыкновенная дробь» на паровозике из «Ромашково».
А девизом к нашему путешествию будут следующие слова:
Дроби всякие нужны,
Дроби всякие важны.
Дробь учи, тогда сверкнет тебе удача.
Если будешь дроби знать,
Точно смысл их понимать, станет лёгкой даже трудная задача.
Прежде, чем отправиться в путешествие, необходимо кое-что вспомнить.
Что такое обыкновенная дробь?
Обратимся к толковому словарю: «Дробь – это число, состоящее из частей единицы».
А что пишут в математической энциклопедии: «Дробь арифметическая – число, состоящее из одной или нескольких равных частей единицы».
Итак, что означает эта запись 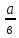 ? (записать на доске)
? (записать на доске)
1). а: в – это частное от деления двух натуральных чисел;
2). целое разделили на в частей и взяли а.
Какие бывают дроби? (дать определение).
правильные,
неправильные,
смешанные числа.
Решим задания на доске и в тетради.
Задание № 1.
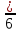 ,
, 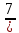 ,
, 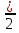 ,
, 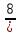 ,
, 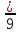 записать правильные дроби;
записать правильные дроби; 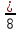 ,
, 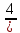 ,
, 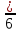 ,
, 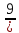 ,
, 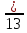 записать неправильные дроби;
записать неправильные дроби;
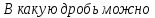 перевести смешанное число? (в неправильную)
перевести смешанное число? (в неправильную)
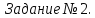 Представьте:
Представьте:
1) смешанное число в виде неправильной дроби: 1 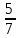 , 3
, 3 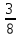 , 5
, 5 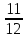 ;
;
2) дробь в виде смешанного числа: 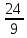 ,
, 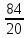 ,
, 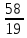 ;
;
Итак, я вижу, что вы готовы отправиться в путешествие.
Едут в страну знаний,
В дальние края
Умные ребята, верные друзья.
Включаем презентацию.
Внимание! Внимание! Паровозик из «Ромашково» отправляется от станции «Школьная» в путешествие по стране «Обыкновенна дробь». На каждой станции за правильное решение заданий вы будете получать по 1 букве слова, которое мы сложим в конце путешествия.
Станция «Решай-ка». (работаем в группах по 4 человека).
Задание № 3.
У Вити на Дне рождения было 5 друзей. Первому он отрезал 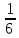 часть пирога, второму -
часть пирога, второму - 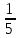 остатка, третьему -
остатка, третьему - 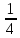 нового остатка, четвёртому -
нового остатка, четвёртому - 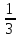 оставшемуся к тому времени куска пирога. Последний кусок Витя поделил с пятым другом пополам. Кому достался самый большой кусок пирога? ( поровну), сделать макет пирога, разрезанного на 6 частей.
оставшемуся к тому времени куска пирога. Последний кусок Витя поделил с пятым другом пополам. Кому достался самый большой кусок пирога? ( поровну), сделать макет пирога, разрезанного на 6 частей.
Покажите
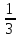 пирога (
пирога ( 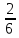 ),
),Покажите
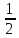 пирога (
пирога ( 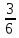 ),
),Покажите
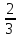 пирога (
пирога ( 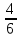 ).
).
Молодцы! Выбираем букву из слова, которое станет известно нам после путешествия, прикрепляем букву на доску магнитом.
Станция «Исторический музей дроби». (читают 2 ученика – экскурсоводы)
В самых древних, дошедших до нас письменных источниках – вавилонских глиняных табличках и египетских папирусах, - встречаются не только целые числа, но и дроби.
Дроби были нужны, чтобы выразить результат измерения длины, когда единица измерения не укладывалась в измеряемой величине целое число раз. Тогда вводили новую, меньшую единицу измерения. Названия этих новых единиц измерения и стали первыми названиями дробей.
Интересная система дробей была в Древнем Риме. Единицу веса, которую называли асс, делили на 12 долей единицы веса. Двенадцатая доля веса называлась унцией. А путь, время и другие величины сравнивались с весом. Например, римлянин мог сказать, что он прошёл 7 унций пути или прочёл 5 унций книги. При этом, имелось ввиду, что пройдено 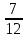 пути или прочитано
пути или прочитано 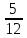 книги. В Древней Греции придумали записывать дроби с помощью числителя и знаменателя, только греки записывали знаменатель – сверху, а числитель – внизу.
книги. В Древней Греции придумали записывать дроби с помощью числителя и знаменателя, только греки записывали знаменатель – сверху, а числитель – внизу.
Впервые в привычном для нас виде дроби стали записывать индусы около 1500 лет назад, но они не использовали черту между числителем и знаменателем. Черту стали употреблять только в XVI веке. Дроби в Древней Руси называли долями, позднее «ломаными числами». В старых руководствах находили следующие названия дробей на Руси:
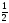 – половина, полтина,
– половина, полтина, 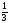 – треть,
– треть,
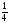 – четь,
– четь, 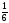 – полтреть,
– полтреть,
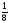 – полчеть,
– полчеть, 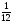 – полполтреть,
– полполтреть,
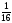 – полполчеть,
– полполчеть, ![]() – полполполтреть (малая треть),
– полполполтреть (малая треть),
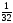 – полполполчеть (малая четь),
– полполполчеть (малая четь), ![]() – пятина,
– пятина,
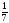 – седьмина,
– седьмина, 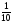 – десятина.
– десятина.
Выбираем букву и отправляемся к следующей станции.
Станция «Сравнилово».
Задание № 4.
Сравни дроби, не приводя к общему знаменателю, сказать правило.
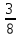 и
и 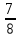 ,
, 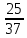 и
и 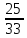 , 2
, 2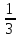 и 2
и 2 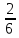 ,
, 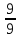 и
и ,
и
,
и
.
Выбираем ещё одну букву неизвестного слова.
Физкультминутка.
Отправляемся дальше в наше путешествие, но вот неприятность – поломка.
Математическая поломка.
Устраните «неисправность» примеров:
Задание №5.
3
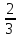 + 5
+ 5 = 8
;
5 – 4
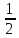 = 1
= 1 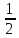 ; Ответы: 1) 9
; Ответы: 1) 9 , 2)
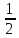 , 3) 5
, 3) 5 .
3
+ 1
= 4
;
Выбираем букву.
Станция «Задачкино».
Решите задачи. Задание № 6.
Почтальону Печкину надо доставить 24 письма. Он уже доставил
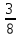 всех писем. Сколько ему ещё осталось доставить? (15 писем )
всех писем. Сколько ему ещё осталось доставить? (15 писем )Суточная норма витамина Е составляет 15 мг, это только
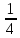 суточной нормы витамина С. Сколько мг витамина С необходимо употреблять в сутки? (60мг)
суточной нормы витамина С. Сколько мг витамина С необходимо употреблять в сутки? (60мг)
Из «Арифметики» Л.Н.Толстого:
Муж и жена брали деньги из одного сундука, и ничего не осталось. Муж взял всех денег, а жена 690 рублей. Сколько было денег в сундуке? (2300 рублей)
Кролик решил на огороде длиной 10 м и шириной 4 м посадить капусту и морковь. Под морковь он занял
площади этого огорода, а остальное – капустой. Какая площадь огорода засеяна капустой?
(15 кв.м)
Задача Пифагора. На вопрос, сколько у него учеников, Пифагор ответил: Половина моих учеников изучают математику, четверть – природу, седьмая часть – проводит время в молчаливых размышлениях, а остальную часть составляют 3 девы. Сколько всего учеников у Пифагора? (28 учеников )
Выбираем букву.
Станция «Тестовая». (с помощью шифра найти буквы, соответствующие правильному ответу, сложить из них слово)
Тест 1.
Найти:
от 36. ( 11, 52 , 28, 21 )
Найти число , если
его равны 20. ( 65, 50, 8, 200 )
Представьте число в виде неправильной дроби 1
.
( ,
,
)
Представьте дробь
в виде смешанного числа.
( 73, 11 , 12
, 73
)
Вычислить
+
( 1
,
,
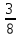 , 1
, 1 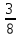 )
)Вычислить
: 3 ( 2,
,
,
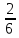 )
) Вычислить
* 5 (
,
1
,
)
Тест 2.
Найти
от 40 . ( 64 , 35, 25, 45)
Найти число, если
его равны 36. ( 81, 16, 18, 8)
Представить число в виде неправильной дроби 1
.
( ,
,
,
)
Представьте дробь
в виде смешанного числа.
( 29, 109, 14 , 14
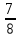 )
)
Вычислить
+
. (
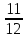 ,
, ,
,
)
Вычислить
: 7 . (
,
,
)
Вычислить
* 3. (
,
,
,
)
Проверить тест, если правильно решили, то получим слова МОЛОДЕЦ и ОТЛИЧНО.
Выбираем букву.
Итак, мы возвращаемся на станцию «Школьная» и на этом наше путешествие заканчивается. Но мы не зря совершили наше путешествие, потому что приобрели ЗНАНИЯ (складываем на доске получившееся слово из добытых букв).
В заключение, хотелось бы привести слова Льва Николаевича Толстого. Он говорил, что «человек подобен дроби, числитель которой есть то, что человек представляет собой, а знаменатель – то, что он думает о себе. Чем большего мнения о себе человек, тем больше знаменатель, а значит, тем меньше дробь».
Дополнительные вопросы, если останется время:
Если дробь равна своему числителю, то чему равен её знаменатель?
Дробь равна своему знаменателю, а чему равен её числитель?
Задание на дом: придумать сказку про обыкновенные дробь.
Приложение.
3

 Получите свидетельство
Получите свидетельство Вход
Вход






























 Урок-игра по математике"Путешествие по стране Обыкновенная дробь" (9.57 MB)
Урок-игра по математике"Путешествие по стране Обыкновенная дробь" (9.57 MB)
 0
0 3703
3703 469
469 Нравится
0
Нравится
0


