Урок алгебры в 9 классе по теме:
«Графический способ решения систем уравнений».
Урок-игра «Восхождение на пик Знаний».
Цель игры: повысить познавательную активность учащихся, привитие интереса к
математике, способствовать развитию внимания, взаимопомощи,
чувства товарищества.
Цель урока: систематизировать и обобщить изученный материал, развивать навыки
решения систем уравнений графически.
Правила игры.
Игровое поле представляет собой рисунок с горным пейзажем и тремя маршрутами восхождения, на которых отмечены привалы, пронумерованные от 1 до 3. Перед началом игры формируются три команды, выбираются капитаны команд. Команды находятся на исходных позициях - базах. Выполнив первое задание, команда может начать движение по маршруту. В случае, если команда быстро и успешно продвигается по маршруту от привала к привалу, то учитель может объявить «спуск снежной лавины», предложив команде коллективно решить сложную задачу. Если эта задача решена, то команда может идти дальше. В противном случае она должна остаться на привале пока не придут «спасатели» (члены другой команды).
Выигрывает та команда, которая правильно выполнит все задания и достигнет «пика Знаний».
Учитель подводит итоги, выставляет оценки отдельно отвечающим учащимся. Капитан команды ведёт маршрутный лист команды, в котором оценивает работу каждого члена команды.
| Маршрутный лист команды №1. |
| |||||||
| № | Список команды | Устно | №1 | №2 | №3 | №4 | Итог | |
| 1 | Бессонов М. | 4 | 5 | 4 | 4 | 3 | 4 | |
| 2 | Петров С. |
|
|
|
|
|
| |
| 3 | Колупаев А. |
|
|
|
|
|
| |
| 4 | Кошман Т. |
|
|
|
|
|
| |
| 5 | Румянцев В. |
|
|
|
|
|
| |
Первый этап - формирование команд, получение маршрутных заданий.
Команда №1 –учащиеся со слабыми способностями.
Команда №2 – учащиеся с хорошими способностями.
Команда №3 – учащиеся с повышенным уровнем знаний.
Второй этап - устные упражнения.
1 команда работает с раздаточным материалом (записать решение системы по рисунку)
|
|
|
|
2 команда работает с математическим лото. Нужно поставить в соответствие систему и
рисунок.
|
|
|
|
|
|
|
|
Карточки для ответов.
|
|
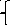
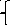
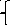
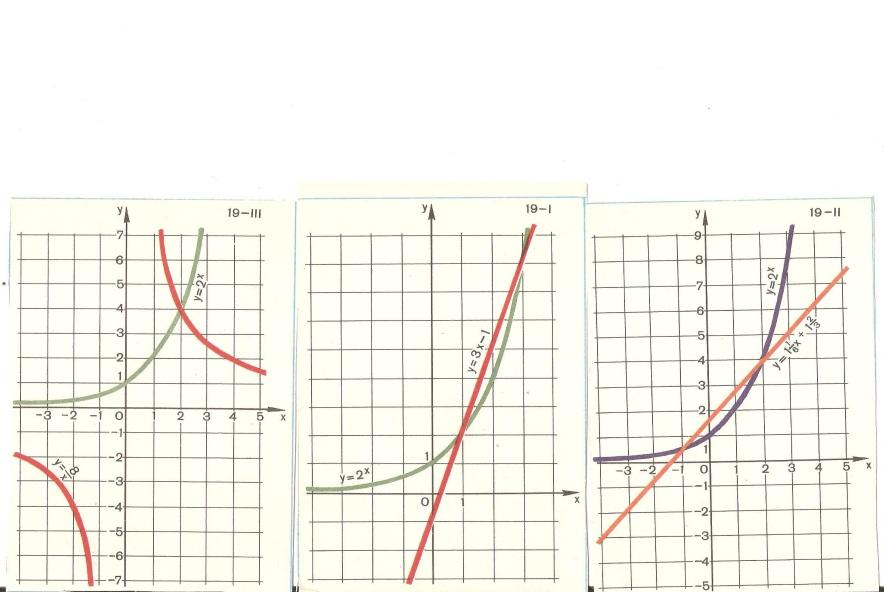
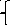 3 команда должна найти ошибки в чертежах, соответствующих системам.
3 команда должна найти ошибки в чертежах, соответствующих системам.
а ) у = х2, б) у = х2, г) у = -6/х, д) у = х2,
х + у = 3. (х -2)2 + у2=4. у =х. у = х3,

Третий этап- восхождение по пик Знаний.
Привал №1.
Решить системы уравнений графическим способом.
 1 команда 2 команда 3 команда.
1 команда 2 команда 3 команда.
 у = -12/х х у = 2 у= х2 – 2х + 1
у = -12/х х у = 2 у= х2 – 2х + 1
у= 5 – 2х 2х – у = 3 у= 2/х
Ответ. 1). (-1,5; 8); (4; -3) 2). (2; 1); (-0,5; -4) 3) ( 2; 1)
Привал №2.
Решить системы уравнений графическим способом.
1 команда 2 команда 3 команда.
 у – х2 =0 у= х2-6х +8 у= х2 +4х -5
у – х2 =0 у= х2-6х +8 у= х2 +4х -5
у – х =0 ху = 12 ху = -6
Ответ. 1) (0;0), (1;1) 2) ≈(4,8; 2,3) 3)≈(-5,2; 1,2)
Привал №3.
Решить системы уравнений графическим способом.
 1 команда 2 команда 3 команда.
1 команда 2 команда 3 команда.
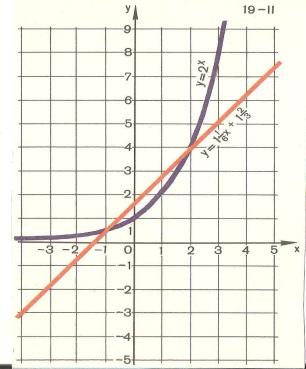
 х – у =2 у= -х2 =6 х2 – 3у = -9
х – у =2 у= -х2 =6 х2 – 3у = -9
у – х2 =2 х2 + у2 = 49 х +у =3
Ответ. 1)решений нет 2) ≈(-3,5; -6) , ≈(3,5 ; -6) 3) (-3; 6), (0; 3)
Привал №4 (общий). Кроссворд.
|
|
|
| 7 | |||||||||||||||||||||||||||||||||||||
|
| 1 |
|
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||
| 6 |
|
|
|
| ||||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||
| 2 |
|
|
|
|
|
|
|
|
|
| 8 |
|
| |||||||||||||||||||||||||||
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||||
|
|
|
| ||||||||||||||||||||||||||||||||||||||
| 3 |
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||
| 4 |
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||||||||
|
|
|
|
|
|
| |||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||
|
|
| 5 |
|
|
|
|
| |||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||
По горизонтали.
1.График функции у=х2. (Парабола)
2.Поверхность, которая получается вращением параболы вокруг её оси.(Параболическая)
3.Что представляет собой график функции х2+ у2= R2. (Окружность)
4.Точка пересечения параболы со своей осью.(Вершина)
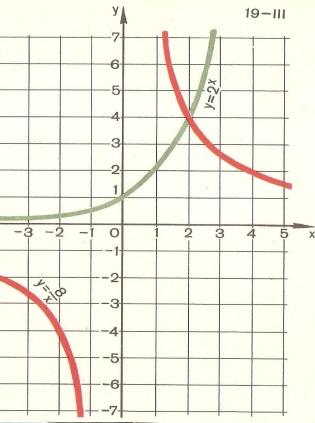
 5.Сколько решений имеет система х2+ у2= 16
5.Сколько решений имеет система х2+ у2= 16
У = х2 – 5 ? ( Четыре)
По вертикали.
4. Направление ветвей параболы у= 3х2. (Вверх).
6.Множество точек плоскости, координаты которых удовлетворяют равенству у=f (х).
(График)
7.Способ решения уравнения или системы. (Графический).
8.Название многочлена второй степени с одной переменной. (Квадратный)
Привал № 5. (Повторение)
Решить уравнение.
1 команда 2 команда. 3 команда.
х2 + х – 210 = 0 х2+ 3х – 88 = 0 7 х2 – 19х +10 =0
Ответ. 1) -15; 14 2) -11; 8 3) 5/7; 2
Привал №6. ( Сообщения учащихся о кривых)
Древнегреческие геометры знали лишь несколько линий, отличных от прямой и окружности. Большинство из них они изучили в связи с тремя знаменитыми задачами древности : об удвоении куба, о трисекции угла и о квадратуре круга.
Геометр Менехм, живший в 4 веке до н.э., описал конические сечения, т.е. кривые, получающиеся при пересечении конуса плоскостью. Он получил три различные кривые в зависимости от того, какой конус он рассекал. Полученные кривые позднее назвали эллипсом, параболой, гиперболой.
Рене Декарт в 1638г придумал новую кривую, уравнение которой имеет вид
х3 + у3 - 3 аху = 0 , а 0.
Её сейчас называют декартовым листом. Через полстолетия Х.Гюйгенс и Иоганн Бернулли установили формулу фигуры симметричную относительно осей координат.
| х|3 + |у|3 -3 а|ху| = 0
Галилей и Декарт изучали циклоиду – кривую, описываемую точкой обода колеса, катящегося по прямой дороге. Та кривая состоит из бесконечного числа арок, каждая из которых соответствует полному обороту колеса. Уравнение одной арки циклоиды имеет вид ________
х= r ∙ arcos r – у _ √ 2 rу - у2
r
Архимед построил особую спираль, определив её на языке механики как траекторию точки, совершающей равномерное и поступательное движение по лучу, который в это время равномерно вращается вокруг своего начала. Уравнение логарифмической спирали в полярных координатах имеет вид: r = аφ
Задания при «сходе снежных лавин».
1) х2 + у2 =16, 2) у + х + х2 =0 3) (х -2)2 + у2=9 4) у=- х2 +4
х – у = 4 х – у = 10 у= х2 – 4х +4 у =|х |
Подведение итога урока. Награждение победителей.

 Получите свидетельство
Получите свидетельство Вход
Вход



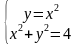
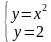
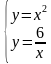
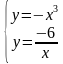
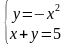
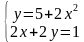
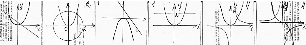









 Урок алгебры в 9 классе по теме: «Графический способ решения систем уравнений». Урок-игра «Восхождение на пик Знаний». (413.21 KB)
Урок алгебры в 9 классе по теме: «Графический способ решения систем уравнений». Урок-игра «Восхождение на пик Знаний». (413.21 KB)
 0
0 200
200 23
23 Нравится
0
Нравится
0


