Цель деятельности учителя.
Создать условия для закрепления знаний учащихся в ходе решения задач и их практического применения, развития логического мышления, формирования исследовательских умений и навыков, личностных, коммуникативных, регулятивных и познавательных УУД.
Дидактические цели урока.
Образовательные: повторить понятия «касательная к окружности», «вписанный прямой угол», «хорда», совершенствовать умения и навыки применять знания об окружности при решении задач, отработать навыки построения, чтения геометрических чертежей
Развивающие: развивать творческую инициативу, умение применять приемы анализа, сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию, развивать устную речь, развивать элементы геометрического мышления, воспитать интерес к оперированию геометрическими понятиями
Воспитательные: воспитывать умение высказывать свою точку зрения, слушать других, принимать участие в диалоге, формировать способность к позитивному сотрудничеству, содействовать формированию внимания, самостоятельности и аккуратности в действиях и выкладках, воспитанию активной творческой личности, умеющей видеть, ставить и решать нестандартные проблемы.
Ход урока.
1 этап. Организационный этап.
Психологическая установка на урок
Приветствие, постановка цели и задач урока. Мотивация учебной деятельности учащихся. Снятие эмоционального напряжения, создание атмосферы открытости и доверительности, направление взаимодействия субъектов педагогического процесса в сторону сотрудничества и позитивного восприятия друг друга.
2 этап. Актуализация опорных знаний и способов действий.
Проверка уровня теоретических знаний, выявление пробелов в знаниях и способах деятельности учащихся
Математический диктант с последующей проверкой
1. Назовите координаты центра, найдите радиус:

а) (х-3) 2+(у-4) 2=16 г) х2+4х+4+у2=25 д) х2+у2=49 е) (х-18) 2 + (у+4) 2 = -36
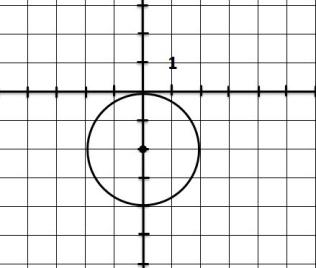
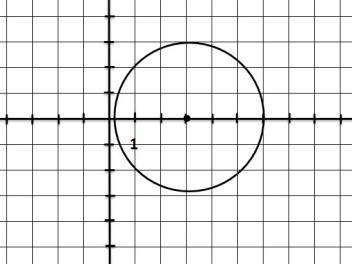
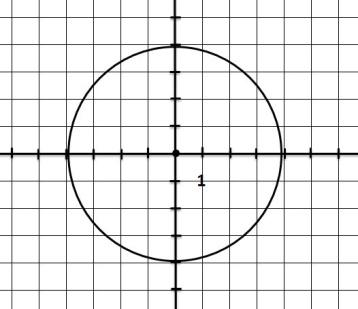
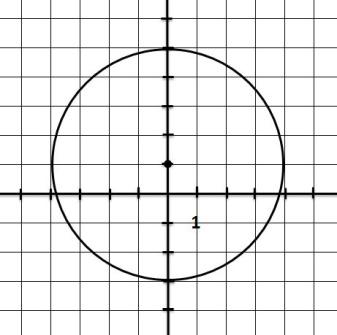
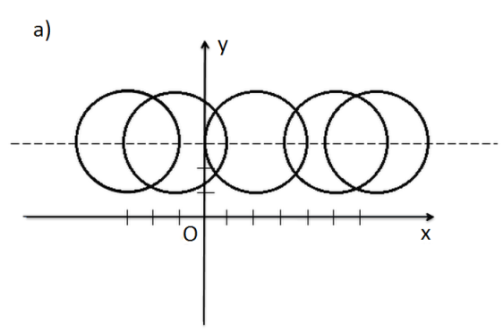
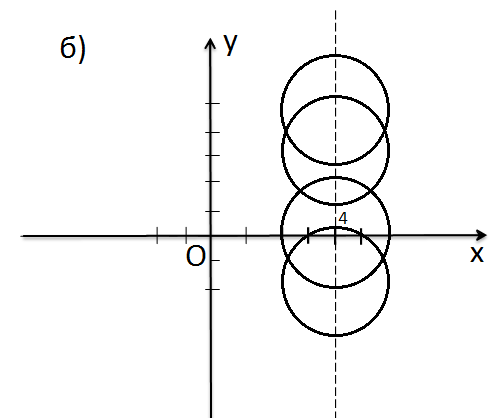
2. найдите по чертежу координаты центра окружности и радиус 3.напишите уравнение окружности с центром в точке (-2;2) и R=11
4. как называется хорда, проходящая через центр окружности?
5. как называется геометрическая фигура, состоящая из множества всех точек плоскости, равноудаленных от данной точки?
Обсуждение результатов математического диктанта, результатов индивидуальной работы по карточкам.
3 этап. Решение задач.
Совершенствование навыков решения задач.
1. Найдите координаты центра окружности, если АВ - диаметр, где А (2;3), В(6;3)
2. Вычислите радиус окружности
3. напишите уравнение окружности, построить окружность
4. найдите точки пересечения окружности с осями координат
5. Укажите, не пользуясь чертежом, какие из точек М(1;7) ; Р(5;2) и А(2;3) лежат:
а) вне круга, ограниченного данной окружностью;
б) на окружности;
в) внутри круга, ограниченного данной окружностью.
Проверьте по чертежу.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



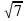 )2=1,44 в) (х+10)2+(у +
)2=1,44 в) (х+10)2+(у +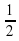 )2 = 5
)2 = 5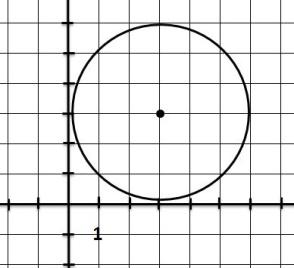
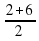 =4; в=
=4; в=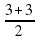 =3; С(4;3)–центр окружности
=3; С(4;3)–центр окружности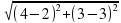 =2
=2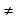 -12;
-12;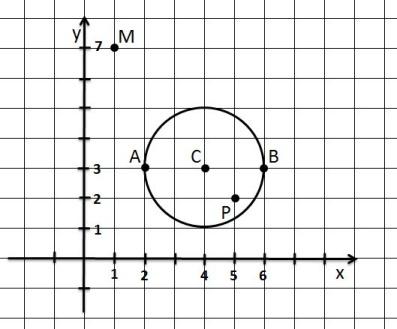
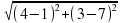 =5
=5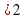
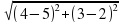 =
=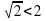
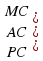 R, то точка
R, то точка 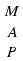 лежит
лежит 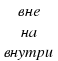
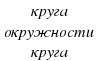









 Уравнение окружности. Решение задач (технологическая карта) (0.36 MB)
Уравнение окружности. Решение задач (технологическая карта) (0.36 MB)
 0
0 1237
1237 171
171 Нравится
0
Нравится
0