Умножение вектора на число

Умножение вектора на число. Гомотетия.

• Прочитать § 4 до задачи 1.
• Ответить на вопросы:

• Что называется произведением ненулевого вектора на число?
• Как найти координаты вектора ka?
• Какими свойствами обладает произведение вектора на число?

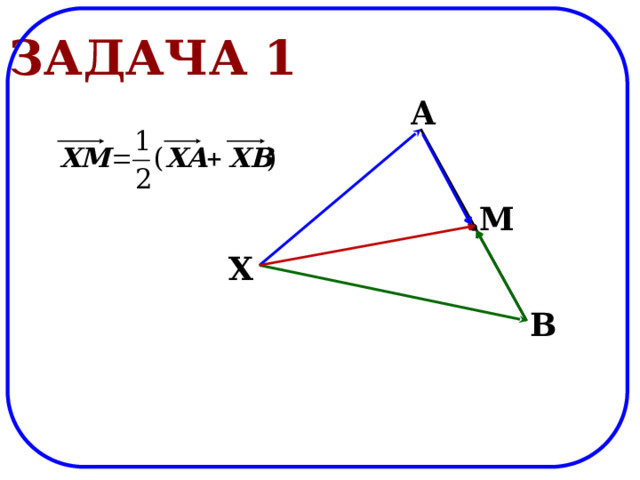
Задача 1

A

M

X

B

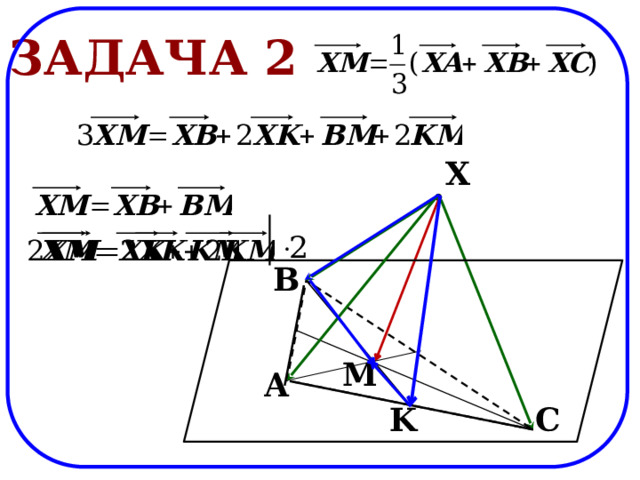
Задача 2

X

B

M

A

C

K

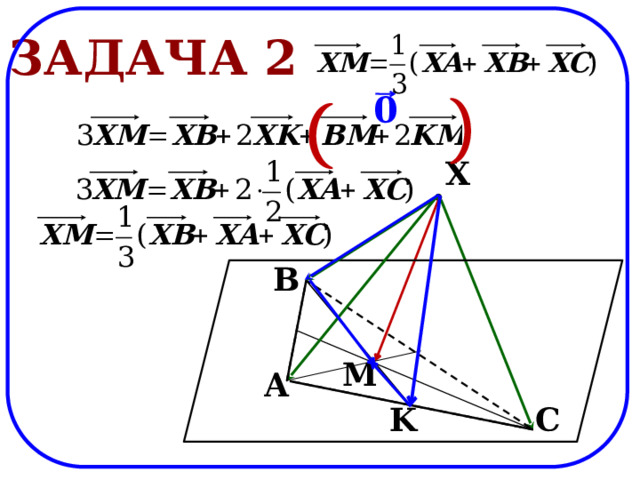
Задача 2

0

X

B

M

A

K

C

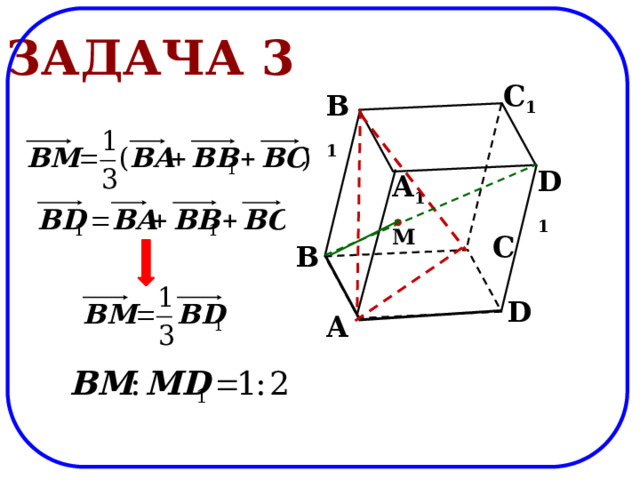
Задача 3

C 1

B 1

D 1

A 1

M

C

B

D

A

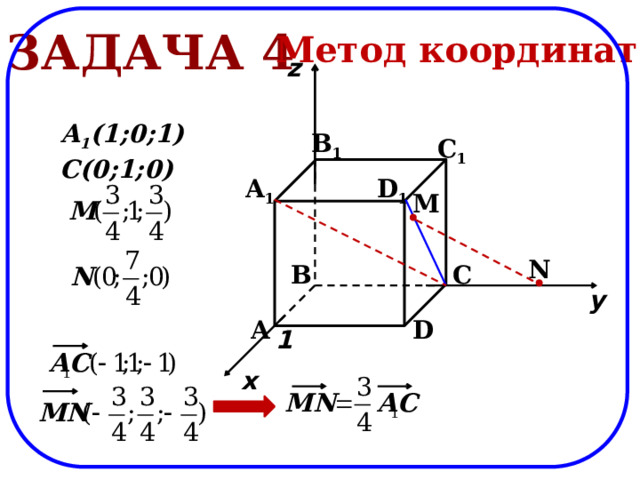
Задача 4

Метод координат

z

A 1 (1;0;1)

B 1

C 1

C(0;1;0)

D 1

A 1

M

N

C

B

y

A

D

1

x

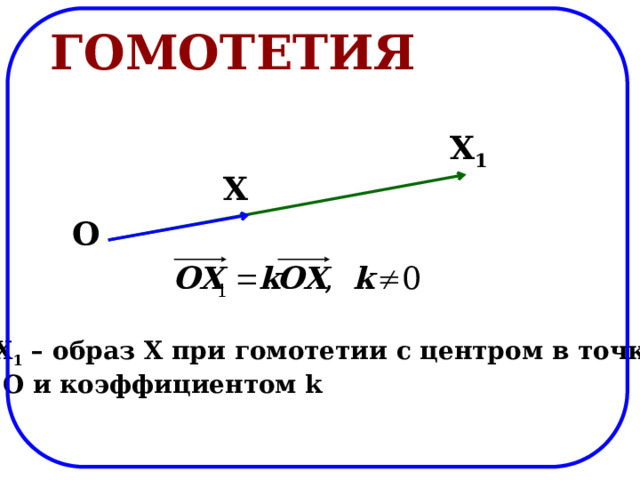
Гомотетия

X 1

X

O

X 1 – образ X при гомотетии с центром в точке

O и коэффициентом k

X 1

X

O

Свойства гомотетии

Образом прямой является данная прямая, если центр гомотетии лежит на этой прямой, и прямая, параллельная данной, если центр гомотетии не лежит на этой прямой.

Образом плоскости является данная плоскость, если центр гомотетии принадлежит этой плоскости, и плоскость, параллельная данной, если центр гомотетии не принадлежит этой плоскости.

Свойства гомотетии

Образом отрезка является отрезок.

Образом угла является угол, равный данному.

Площадь многоугольника изменяется в k 2 раз, где k – коэффициент гомотетии.

Решение задач:

№№ 1, 2, 3, 4, 6, 8, 10, 12, 14.

Решение задач:

№№ 5, 7, 9, 11, 13, 15.