Угол между прямой и плоскостью. Теорема о трёх перпендикулярах

Угол между прямой и плоскостью. Теорема о трёх перпендикулярах

Вопросы:

1. Угол между прямыми равен 90 º . Как называются такие прямые?

/перпендикулярные/

2. Верно ли утверждение: « Прямая называется перпендикулярной плоскости, если она перпендикулярна некоторой прямой, лежащей в этой плоскости » ?

/да/

3. Сформулируйте признак перпендикулярности прямой и плоскости.

/Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости./

4. Как определяется расстояние от точки до прямой на плоскости

/как длина перпендикуляра, поведенного из точки к данной прямой./

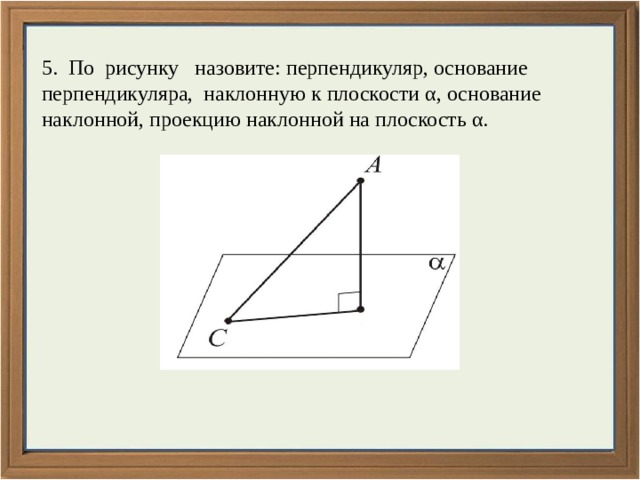
5. По рисунку назовите: перпендикуляр, основание перпендикуляра, наклонную к плоскости α, основание наклонной, проекцию наклонной на плоскость α.

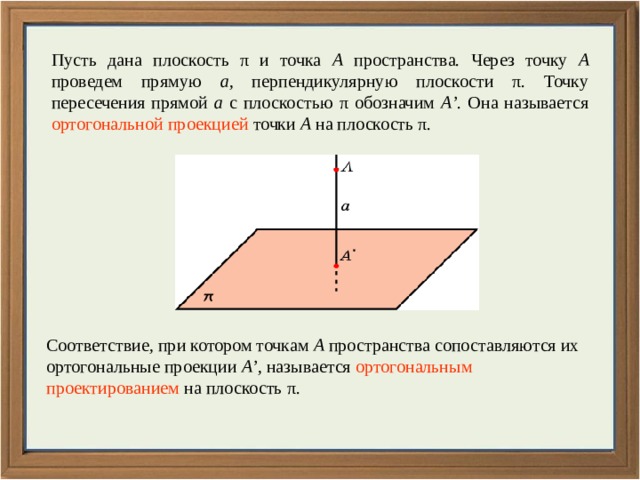
Пусть дана плоскость π и точка A пространства. Через точку A проведем прямую a , перпендикулярную плоскости π. Точку пересечения прямой a с плоскостью π обозначим A’ . Она называется ортогональной проекцией точки A на плоскость π.

Соответствие, при котором точкам A пространства сопоставляются их ортогональные проекции A’ , называется ортогональным проектированием на плоскость π.

Свойство 1. Если прямая перпендикулярна плоскости проектирования, то ее ортогональной проекцией является точка. Если прямая не перпендикулярна плоскости проектирования, то ее ортогональной проекцией является прямая.

Свойство 2. Ортогональное проектирование сохраняет отношение длин отрезков, лежащих на одной прямой. В частности, при ортогональном проектировании середина отрезка переходит в середину соответствующего отрезка.

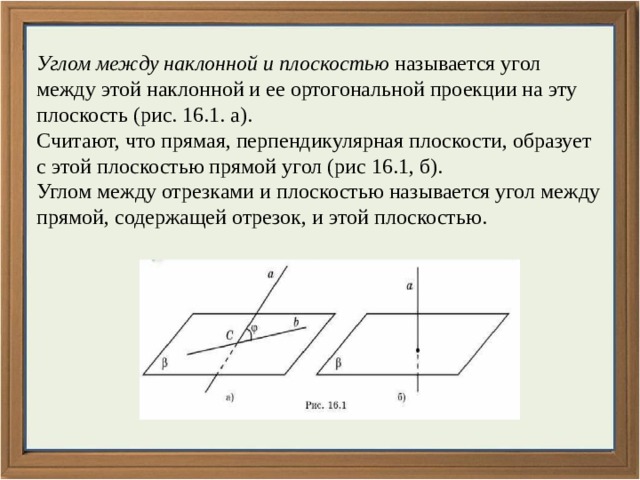
Углом между наклонной и плоскостью называется угол между этой наклонной и ее ортогональной проекции на эту плоскость (рис. 16.1. а).

Считают, что прямая, перпендикулярная плоскости, образует с этой плоскостью прямой угол (рис 16.1, б).

Углом между отрезками и плоскостью называется угол между прямой, содержащей отрезок, и этой плоскостью.

Теорема о трех перпендикулярах

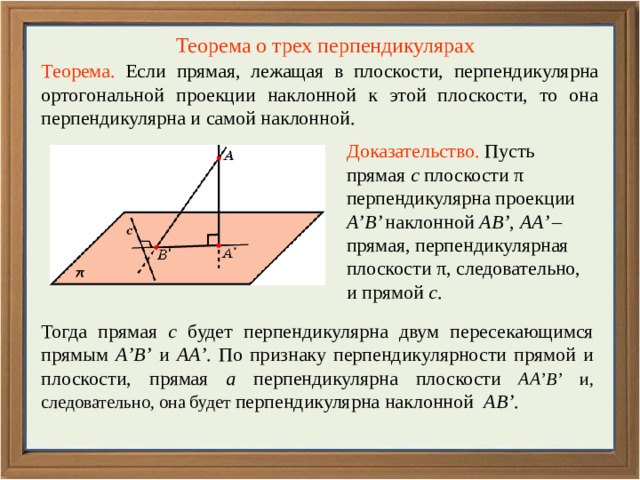
Теорема. Если прямая, лежащая в плоскости, перпендикулярна ортогональной проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной.

Доказательство. Пусть прямая c плоскости π перпендикулярна проекции A’B’ наклонной AB’ , AA’ – прямая, перпендикулярная плоскости π, следовательно, и прямой c .

В режиме слайдов ответ появляется после кликанья мышкой.

Тогда прямая c будет перпендикулярна двум пересекающимся прямым A’B’ и AA’ . По признаку перпендикулярности прямой и плоскости, прямая а перпендикулярна плоскости АA’В’ и, следовательно, она будет перпендикулярна наклонной АВ’ .

Верно и обратное. А именно, если прямая, лежащая в плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и ортогональной проекции этой наклонной. Попробуйте доказать это самостоятельно.

Пример. Докажите, что в кубе ABCDA l B l C l D J прямые АС и BD 1 перпендикулярны (рис. 15.5).

Решение. Ортогональной проекцией прямой BD 1 на плоскость ABC является прямая BD (рис. 15.6). Прямая АС перпендикулярна BD, следовательно, она перпендикулярна BD 1 .