Учебно-практическая работа "Правильные многогранники"

УЧЕБНО-ПРАКТИЧЕСКАЯ РАБОТА ПО МАТЕМАТИКЕ ПРАВИЛЬНЫЕ МНОГОГРАННИКИ

Выполняли:

Валерия Рахманова

Костырко Марина

Попова Алиса

6 Б класса

Выполнили:

Рахманова Валерия

Костырко Марина

Попова Алиса

учащиеся 6 «Б» класса

МАОУ «СОШ №2»

Г.Первоуральск

Учитель:

Глазачева Галина

Александровна

ЦЕЛЬ РАБОТЫ

• Изготовить из бумаги развёртки и склеить модели 5 правильных многогранников.

• Исследовать по изготовленной модели каждого многогранника форму его граней и их число, число вершин и рёбер, а так же их число при одной вершине.

Задачи

1) Изучить учебный материал по данной теме на стр.210-211 учебника и расширить знание о правильных многогранниках за его пределами :

• определение, виды, элементы правильного многогранника;
• история возникновения правильных многогранников;
• в каком виде можно встретить модели правильных многогранников в окружающем мире.

2) Построить бумажные развертки и склеить многогранники , исследуя формы и число их элементов на основе этого наблюдения заполнить таблицу, запечатлеть на фото результаты практической работы.

3) Обобщить , систематизировать и представить результаты данной работы в виде электронной презентации

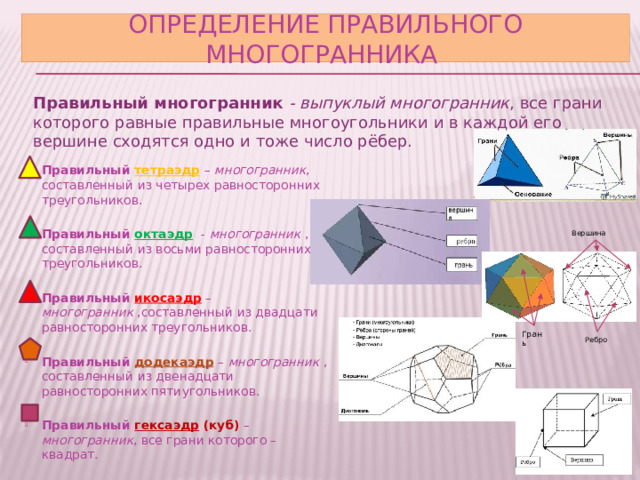
Определение Правильного многогранника

Правильный многогранник - выпуклый многогранник , все грани которого равные правильные многоугольники и в каждой его вершине сходятся одно и тоже число рёбер.

• Правильный тетраэдр – многогранник , составленный из четырех равносторонних треугольников.

• Правильный октаэдр - многогранник , составленный из восьми равносторонних треугольников.

• Правильный икосаэдр – многогранник ,составленный из двадцати равносторонних треугольников.

• Правильный додекаэдр – многогранник , составленный из двенадцати равносторонних пятиугольников.

• Правильный гексаэдр (куб) – многогранник , все грани которого –квадрат.

Вершина

Грань

Ребро

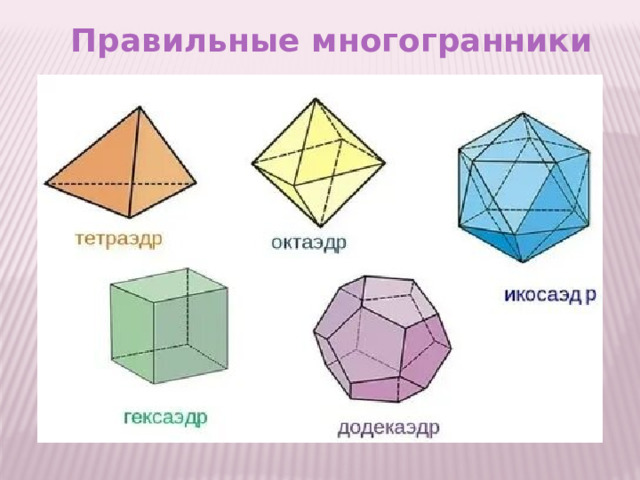
Правильные многогранники

История возникновения правильных многогранников

Правильные многогранники были известны людям с древнейших времён. Их вырезанные изображения можно найти на каменных шарах в Шотландии. В игральных костях, которыми пользовались люди на заре цивилизации, уже можно было рассмотреть формы правильных многогранников.

Довольно подробно правильные многогранники были изучены древнегреческими учёными. По некоторым источникам честь их открытия принадлежит Пифагору. Другие же источники утверждают, что Пифагору были знакомы только тетраэдр, куб и додекаэдр , а открытие октаэдра и икосаэдра принадлежит Теэтету Афинскому , современнику Платона.

В XVI веке немецкий астроном Иоганн Кеплер пытался найти связь между пятью известными на тот момент планетами Солнечной системы, исключая Землю, и правильными многогранниками. В своей книге «Тайна мира», вышедшей в 1596 году, он изложил свою модель Солнечной системы.

Где встречаются правильные многогранники

1) Икосаэдро -додекаэдровая структура Земли. Ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов.

2)Правильные многогранники в живой природе . Например, скелет одноклеточного организма феодарии по форме напоминает икосаэдр .

3)В технике . Тетраэдр , выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм мостов.

Практическая часть

Фоторепортаж

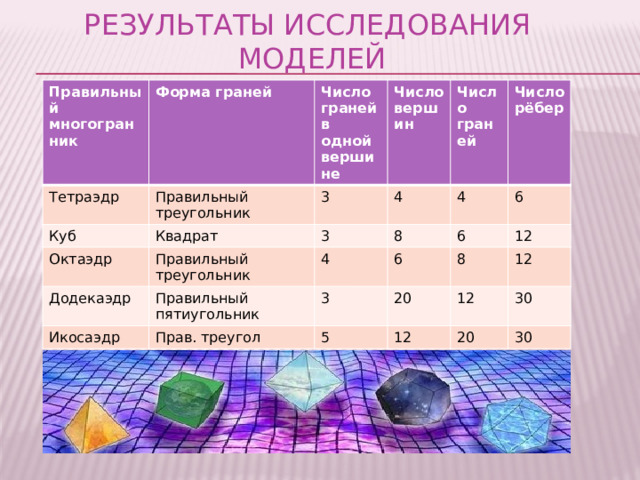
Результаты исследования моделей

Правильный многогранник

Форма граней

Тетраэдр

Правильный треугольник

Число граней в одной вершине

Куб

Квадрат

Октаэдр

Число вершин

3

Число граней

3

4

Правильный треугольник

Додекаэдр

4

4

Число рёбер

8

Икосаэдр

Правильный пятиугольник

6

6

6

3

Прав. треугол

8

12

20

5

12

12

12

30

20

30

Выводы

• Цель достигнута. Удачное изготовление развёртки и склеивание многогранников.
• Задачи выполнены.Изученный учебный материал был нами усвоен.Мы познакомились с историей возникновения правильных многогранников.
• Трудности возникли со склейкой фигур и созданием таблицы.
• Нам очень понравился процесс создания презентации . Мы получили удовольствие от совместной работы.

Эту тему я считала

… Многогранник правильный—

Особого рода

Лишь геометрической,

И, представьте, связан

А теперь её я знаю

Тесно он с природой.

С точки исторической.

Биологи и химики

Древнегреческий мыслитель

Об этом в книге написал.

Дружат с этой темой,

Географы, геологи               

Многогранники учёный

Гадают над проблемой.

Со стихиями связал.

Куб — Земля, октаэдр — воздух,

В теме «Многогранники»

Столько есть секретов.

Икосаэдр — вода,

Заслуживает тема,

А тетраэдр — огонь,

Чтоб говорить об этом!

Ты попробуй его тронь!

Этот с виду очень важный,

Додекаэдр зовётся.     

Вселенную он представляет,

Где ещё такой найдётся!...

Автор материала в стихах

Болотнева Наталья Васильевна

https://infourok.ru/stihotvorenie-dlya-uroka-geometrii-v-starshih-klassah-1541220.html