Учебно-методическое пособие по теме "Системы счисления"

26

Государственное бюджетное образовательное учреждение
средняя общеобразовательная школа 562
Красногвардейского района

КОДИРОВАНИЕ ИНФОРМАЦИИ

г. Санкт-Петербург

2017

Кодирование информации (учебно-методическое пособие для учителей и учащихся)

Автор: Дершевич О. М., учитель информатики и ИКТ ГБОУ СОШ 562 Красногвардейского района г. Санкт-Петербурга

Содержание

Системы счисления 3

Позиционные системы счислени

4

Двоичная система счисления 5

Метод разностей 6

Связь 8-ричной системы счисления с двоичной 7

Связь 16-ричной системы счисления с двоичной 8

Перевод дробных чисел 10

Задания для самостоятельного решения 12

Методическое пособие рассмотрено и одобрено на заседании методиче­ского объединения учителей технического направления ГБОУ СОШ 562, протокол № 1 от 30.08.2017 г.

1. Системы счисления

Система счисления – это совокупность приёмов и правил изображения чисел цифровыми знаками.

Позиционные системы – это системы, в которых значение числа зависит не только от начертания цифры, но и от её положения в кодовой комбинации.

В непозиционных системах значение числа не зависит от положения цифры в кодовой комбинации.

Смешанная система содержит элементы как позиционной, так и непозиционной систем (римская система счисления)

Системы счисления

Позиционные Непозиционные Смешанные

1. Чёрточки и палочки

2. Древнерусская запись чисел

3. Алфавитная нумерация у славян

Пример записи числа в Древней Руси: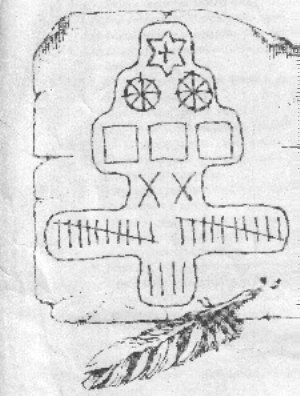

1232 руб 24 коп

Алфавитная нумерация у славян:

Например, TKД = 324

В смешанной Римской системе счисления используются следующие символы:

I	V	X	L	C	D	M
1	5	10	50	100	500	1000

Например 1998=MCMXCVIII

Задание1. Запишите по правилам Древней Руси:

2143 руб и 13 коп;

113 руб и 61 коп;

Задание 2. Запишите, используя алфавитную нумерацию славян числа:

523, 841.

Задание 3. Запишите римскими цифрами числа:

2007, 18 и год своего рождения.

1. Позиционные системы счисления

В десятичной системе счисления 10 – называется основанием системы. Любое число можно представить следующим образом:

159=1*10²+5*10¹+9*10⁰

Формула представления чисел в позиционных системах счисления:

N = a_nb^n-1+ a_n-1b^n-2 + …+ a₁b⁰

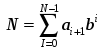
a_i – количество единиц в разряде i,

N – количество разрядов числа,

b – основание системы счисления.

Задание 4.

Разложить по степеням основания системы счисления следующие числа:

1247₁₀=

1247₈=

Задание 5.

Представить заданные числа в десятичной системе счисления:

312₄=

514₆=

222₃=

Задание 6.

Перевести заданные числа из десятичной в другие системы счисления.

Например, 159₁₀=1114₅

159 155	5
	31 30	5
4		6 5	5
	1		1
		1

Перевести числа:

186₁₀=?₅

93₁₀=?₄

Задание 7.

Перевести заданные числа из десятичной в другие системы счисления.

161₁₀=?₈

150₁₀=?₇

60₁₀=?₂

Задание 8.

Перевести заданные числа из других систем счисления в десятичную.

140₁₀=?₄

58₁₀=?₈

37₁₀=?₇

1. Двоичная система счисления

«В своей бинарной арифметике Лейбниц видел прообраз творения. Ему представлялось, что единица представляет божественное начало, а нуль – небытие и что высшее существо создаёт всё сущее из небытия точно таким же образом, как единица и нуль в его системе выражает числа»

П. С. Лаплас

1. Выписать в тетрадь степени двоек.

2⁰ 2¹ 2² 2³ 2⁴ 2⁵ 2⁶ 2⁷ 2⁸ 2⁹ 2¹⁰

1 2 4 8 16 32 64 128  256 512 1024

2. Преимущества двоичной системы:

1) минимальный алфавит

2) простота технической реализации (вкл./выкл.)

3) высокая помехоустойчивость (можно дать больший разброс электрического тока)

4) простота арифметических действий

Таблица умножения:

0*0=0

0*1=0

1*0=0

1*1=1

1. Недостатки: быстрый рост числа разрядов (длинные числа).

Арифметические действия в двоичных системах .

1+0=1 10 – 1=1

1+1=10 100 – 1=11

1+1+1=11

1+1+1+1=100

Задания.

111100 + 10111 =

111 0011 – 1011 =

101101 x 1010 =

10110 :11 =

1. Метод разностей

Задание. Перевести число 1579 из 10-тичной в 2-ичную систему.

Используем метод разностей. Рассмотрим ближайшую степень двойки: 1024 (2¹⁰). Остаток: 1579 – 1024 = 555

	Ближайшая степень двойки	Остаток
1579	1024 = (210)	1579 – 1024 = 555
555	512 = (29)	555 – 512 = 43
43	32 = (25)	43 – 32 = 11
11	8 = (23)	11 – 8 = 3
3	2	1

10	9	8	7	6	5	4	3	2	1	0
1	1	0	0	0	1	0	1	1	0	0

Ответ: 11000101100

Задания.

Перевести числа из 10 –тичной в 2 –ичную систему:

1. 345

2. 654

3. 45

4. 1269

5. 810

Двоично-десятичный код

Двоично-десятичный код предназначен для кодирования десятичных чисел последовательностью нулей и единиц. Наиболее часто двоично-десятичный код применяется для ввода в машину исходных данных, записных в десятичной системе счисления. После ввода в ЭВМ двоично-десятичный код самой машиной переводится в двоичную систему счисления.

Пример

1) 0101 0111 0011,0100₁₀ =573,4_2-10

5 7 3 4

2)362,89₁₀ = 11 0110 0010,1000 1001_2-10

3 6 2 8 9

1. Связь восьмеричной системы счисления с двоичной

Восьмеричная цифра	Двоичное число
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

Правило перевода числа, представленного в 8 системе в двоичную:

каждую цифру восьмеричной записи следует заменить её двоичным представлением (соответствующей двоичной триадой).

475₈ = 100 111 101, так как 100 = 4, 111 = 7, 101 = 5.

317₈ = 011 001 111

Правило перевода числа, представленного в 2 системе в восьмеричную:

в двоичной записи числа нужно выделить триаду (справа налево) и заменить каждую триаду восьмеричной цифрой. В случае необходимости слева добавить нули.

1010110 = 001 010 110 = 126₈

11 110 100 =364₈

Задания.

1. Перевести числа 345, 3366, 277 из 8-ричной в 2-ичную систему счисления.

1. Перевести числа 1001111001, 1000110111, 10101 из 2-ичной в 8-ричную систему счисления.

1. Связь шестнадцатеричной системы счисления с двоичной

Назначение 16-ричной системы аналогично 8-ричной – для компактной записи двоичных кодов чисел и команд. Содержимое ячеек памяти (это 8-разрядные двоичные числа) представляются в 16-ричной системе в виде всего двухразрядных чисел.

В 16-ричной системе используются буквы латинского алфавита A,B,C,D,E,F, для обозначения соответственно чисел 10,11,12,13,14 и 15.

Правило перевода числа, представленного в 16-системе в двоичную и обратно:

каждую 16-ричную цифру нужно заменять соответствующей двоичной тетрадой.

Примеры:

15 = F

31 = 1F

167 = A7

6C = 0110 1100

11111011111 = 0111 1101 1111 = 7DF

Десятичные цифры	Шестнадцатеричная запись	Двоичная запись
0	0	0000
1	1	0001
2	2	0010
3	3	0011
4	4	0100
5	5	0101
6	6	0110
7	7	0111
8	8	1000
9	9	1001
10	A	1010
11	B	1011
12	C	1100
13	D	1101
14	E	1110
15	F	1111

Задания.

1. Перевести числа 3D5, F33, 27A из 16-ричной в 2-ичную систему счисления.

1. Перевести числа 1001111001, 1000110111, 10101 из 2-ичной в 16-ричную систему счисления.

Перевод чисел из систем счисления с основанием 2^N
в двоичную систему счисления и обратно.

Общее правило: каждую цифру данного числа нужно заменить её n-значным эквивалентом в 2-ичной системе счисления.

Обратно: Данное двоичное число разбить справа налево на группы по n цифр в каждой и рассмотреть каждую группу как n-разрядное двоичное число, чтобы записать её соответствующей цифрой в заданной системе счисления.

Задания. Рассмотреть примеры с 4-ричной системой счисления.

1. Перевод дробных чисел из одной системы счисления в другую

Перевод дробных чисел в десятичную систему.

Дробные числа в десятичной системе представляются так:

0,375₁₀=3* 1/10 + 7 * (1/10)² + 5 * (1/10)³

В восьмеричной системе так:

0,375₈= 3 * 1/8 + 7 * (1/8)² + 5 * (1/8)³

0,2754₈= 2 * 1/8 + 7 * (1/8)² + 5 * (1/8)³ + 4 * (1/8)⁴

Но 1/8 = 0,125₁₀.

Отсюда следует, что 0,2754₈= 2 * 0,125 + 7 * 0,125² + 5 * 0,125⁴=

= 0,250 +0,109375 +0, 009765625 + 0,0009765625=0,3701171875₁₀

II

Перевод дробных чисел из десятичной системы в другую.

Задание 1. Пусть дана десятичная дробь 0,423828125, которую нужно перевести в восьмеричную систему.

Чтобы найти первую после запятой цифру восьмеричную дроби, нужно узнать, сколько восьмых содержится в заданном числе. Для этого можно поступить так: предварительно умножить заданное число на восемь и узнать, сколько целых содержится в полученном произведении. Так как

0,423828125 * 8= 3,390625000,

то целая часть произведения содержит 3 единицы, а стало быть, само данное число содержало 3 восьмых. Иначе говоря, первой после запятой восьмерично цифрой числа будет цифра 3. Аналогично рассуждая, получаем другие цифры.

0,│456 0546875

│ *8

3,│6484375000

│ *8

5,│1875000

│ *8

3,│5000

│ 8

4,│0

Задание 2. Перевести число 0 ,65625₁₀ в шестнадцатеричную систему счисления.

0, │65625

│ *16

10 │ 50000

(А) │ *16

8 │ 00000

0,65625₁₀ = 0,А8₁₆

Правило перевода:

1) последовательно умножать данное число и получаемые дробные части произведений на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа;

2) полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.

При переводе смешанных чисел отдельно переводятся целые и дробные части:

124,8₁₀=174,2₈

Задания.

1. Переведите числа из десятичной системы счисления в восьмеричную:

1) 0,43 2) 37,41 3) 2936 4) 481,625

2. Переведите числа из десятичной системы счисления в шестнадцатеричную:

1) 0,17 2) 43,78 3) 25,25 4) 18,5

1. Задачи для самостоятельного решения

1.

Вычисление суммы чисел х=1D₁₆ и у=72₈.

Результат перевести в двоичную систему исчисления.

1. 10001111₂

2. 1100101₂

3. 1010111₂

4. 101011₂

2.

Как представить число 83₁₀ в двоичной системе?

1. 1001011₂

2. 1100101₂

3. 1010011₂

4. 101001₂

3.

Вычислите сумму двоичных чисел Х и У, если

х=1010101₂
у=1010011₂

1. 10100010

2. 10101000

3. 10100100

4. 10101000

4.

Количество значащих нулей в двоичной записи

126₁₀=?

1. 1

2. 2

3. 3

4. 0

5.

В какой системе счисления 2+2=11?

6.

В какой системе счисления 10-нечётное?

7.

Задача «Автобиография математика»

Я окончил курс университета 44 лет отроду.

Спустя год, 100-летним молодым человеком, я женился на 34-летней девушке.
Незначительная разница в возрасте, всего 11 лет, способствовала тому, что мы жили одними интересами. Спустя немного лет, у меня уже была семья из 10 детей. Жалованье я получал всего 200 рублей. Из которых 1/10 приходилась отдавать сестре. Так что мы с детьми жили на 130 рублей в месяц. В какой системе счисления ведется повествование?

Используемая литература

1. Информатика, 10-11, Л. З. Шауцукова, «Просвещение», 2004

2. Информатика. Базовый курс, 9 кл., И. Семакин, БИНОМ, 2015