"Центральные и вписанные углы"

Учитель: Краснова Т.Н.

Класс: 8

Тема: Решение задач по теме «Центральные и вписанные углы»

Тип урока:

Урок применения предметных знаний, умений и навыков.

Цель: отработать навыки решения задач на применение понятий вписанного и центрального углов, на применение теоремы о вписанном угле и её следствий.

Задачи:

Обучающие: решать задачи на нахождение градусной меры угла, дуги; решать задачи из ОГЭ; выполнять тест.

Развивающие: реализация принципов связи теории и практики, развивать способности анализировать, проводить наблюдения, развитие познавательного интереса, творческой самостоятельности мышления учащихся, развитие математической речи.     

Воспитательные:  активизация самостоятельности познавательной деятельности учащихся; формирование умений осуществлять взаимоконтроль, самоконтроль; формирование навыков коллективной работы, развитие чувства ответственности за свои знания.

Планируемые результаты: владение изученным материалом, умение применять теоретический материал при решении практических задач.

Формы деятельности: парное обучение, групповое обучение

Методы и приёмы: сочетание словесных, наглядных и практических, репродуктивных и проблемно-поисковых; работа под руководством учителя и самостоятельная работа учащихся.

Педтехнологии: ИК - технологии, сотрудничества, проблемное.

Оборудование: компьютер, мультимедийный проектор, карточки с заданиями.

Ход урока

1. Организационный этап

Задачи этапа: включить учащихся в учебную деятельность

Здравствуйте. Рада видеть вас в хорошем настроении. Сегодня мы в очередной раз отправимся в увлекательный мир математики. (Слайд № 2)

Хочется напомнить народную мудрость "Ум без догадки - гроша не стоит", т.к. при решении геометрических задач нужна смекалка, умение рассуждать, анализировать, а это невозможно без знаний и вдохновения. Вдохновения вам на протяжении всего урока.

Откройте тетради, запишите дату, классная работа.

- Что изучали на прошлом уроке?

Ответ: Мы изучили: - понятие центрального и вписанного угла;

- свойства центрального угла;

- свойства вписанного угла и следствия из него.

А сегодня цель урока?

- научиться применять понятие вписанного и центрального углов, теорему о вписанном угле и её следствий при решении задач.

Для достижения этой цели, какие задачи поставим.

- повторить теоретический материал;

- решение задач на нахождение градусной меры угла, дуги;

- решение задач на связь центральных и вписанных углов.

- решать задачи из ОГЭ; (т.к такие задачи есть в ОГЭ)

- выполним тест. (Слайд № 3)

- Сформулируйте тему урока.

Запишите тему урока «Центральные и вписанные углы. Решение задач»

- Не забывайте оценивать себя.

У вас есть маршрутный лист. После выполнения каждого задания и его проверки, вы подсчитываете и заносите результат в таблицу, в конце урока их суммируете. Выполнять все задания нужно дружно, быстро и спокойно, чтобы не мешать другим.

1. Актуализация знаний

Задачи этапа: повторить теоретический материал, подготовить учащихся к решению задач.

- Внимание на экран. На какие группы вы бы разделили углы (Слайд № 4)

Понятие угол и окружность появилось много веков назад. Инженеры и математики древности пользовались этими понятиями при построении различных архитектурных сооружений. Так же эти понятия использовались при навигации на море и на суше. В наше время понятие и свойство центральных и вписанных углов используется в науке и технике. Например, невозможно представить себе без этих понятий современную инженерную графику и машиностроение. В астрономии для вычисления параллакса.

1. Устная работа

*Теоретические вопросы

Вопросы: (вначале проговаривают в парах друг другу, затем кто-то говорит вслух)

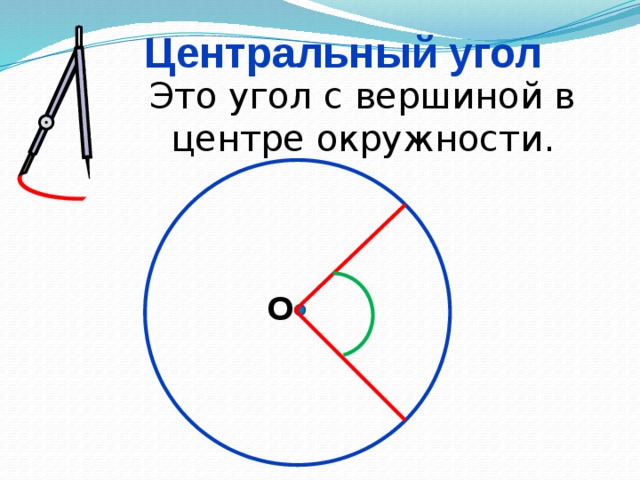
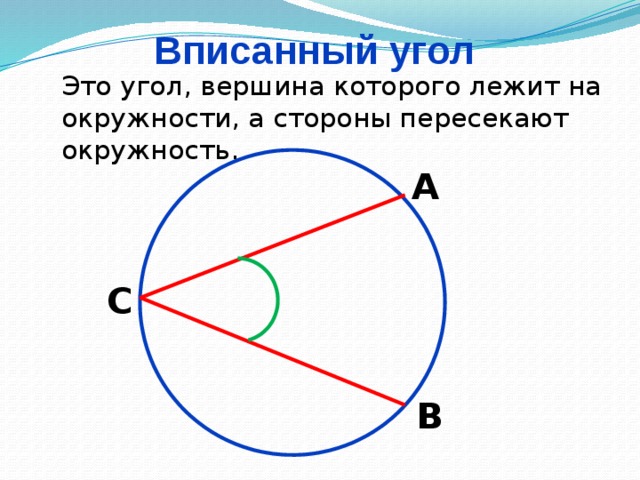
• Какой угол называется центральным? (Слайд №5)

• Каким соотношением связаны центральный  угол и дуга, на которую он опирается?

• Дайте определение вписанного угла треугольника. (Слайд № 6, 7)

• Какая теорема выражает его свойство? (взаимопроверка)

*Устные упражнения (по слайдам)

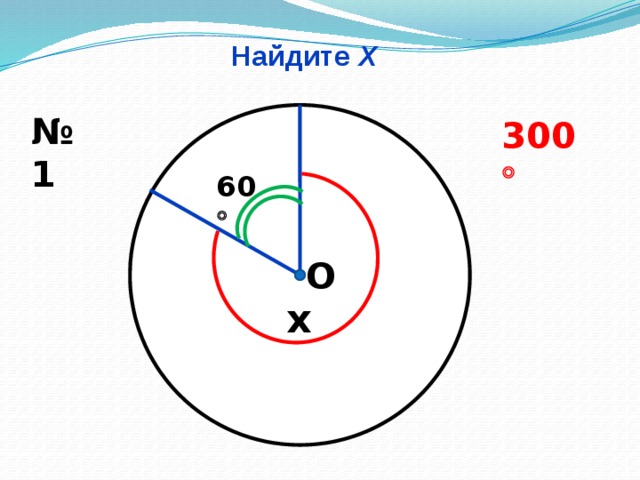
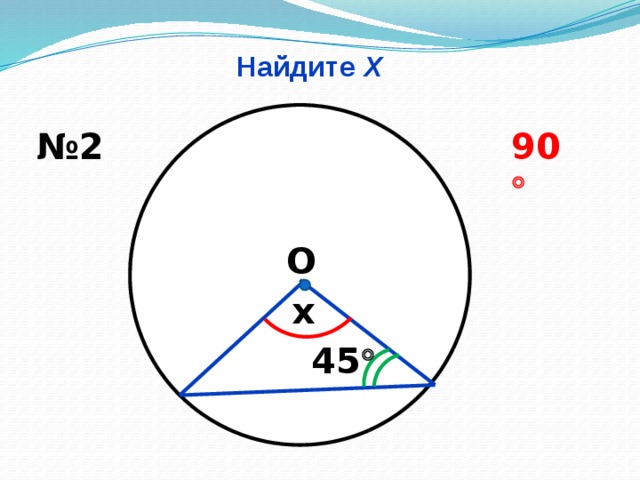
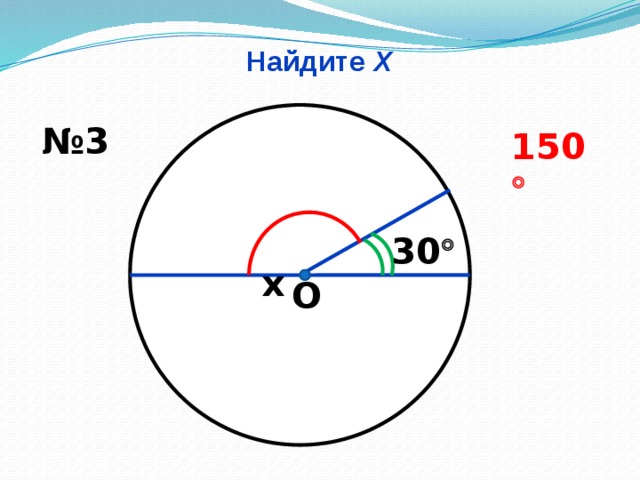
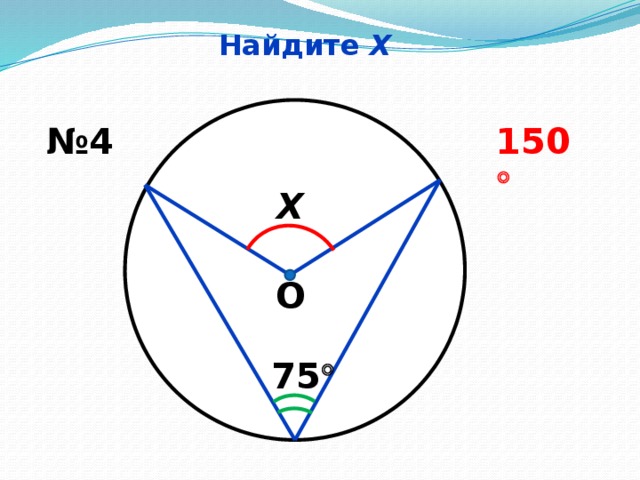
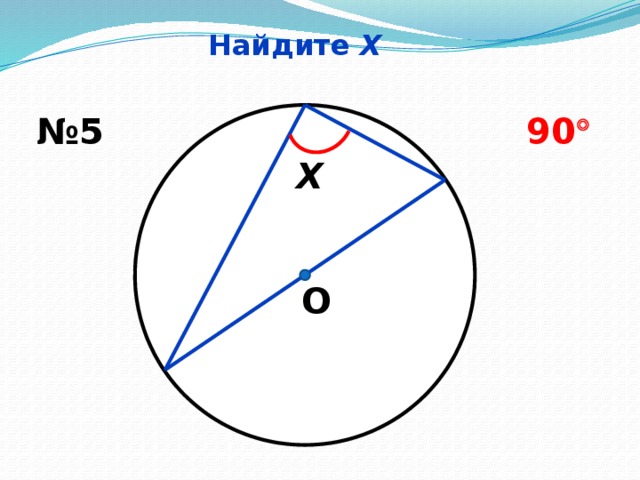
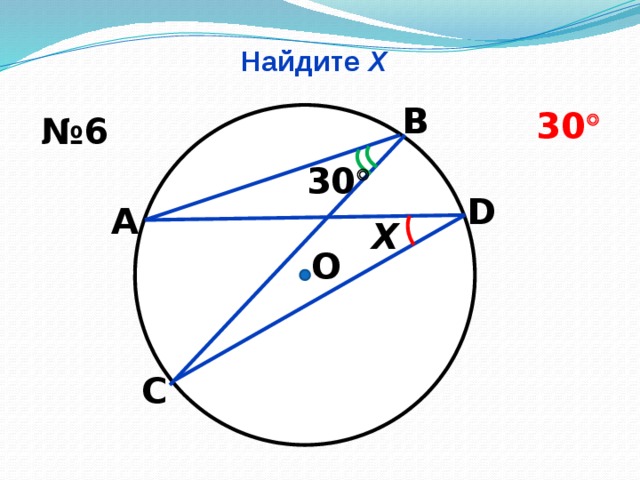
Найдите Х (Слайд № 8, 9, 10, 11, 12.13)

Учащиеся на слайдах видят только рисунок. Используя данные рисунка, учащиеся находят неизвестное. И только после выполнения задания учитель проектирует на экран правильные ответы, учащиеся комментируют решение.

III Закрепление

Задачи этапа: применить опорные знания на практике; прививать навыки самоконтроля.

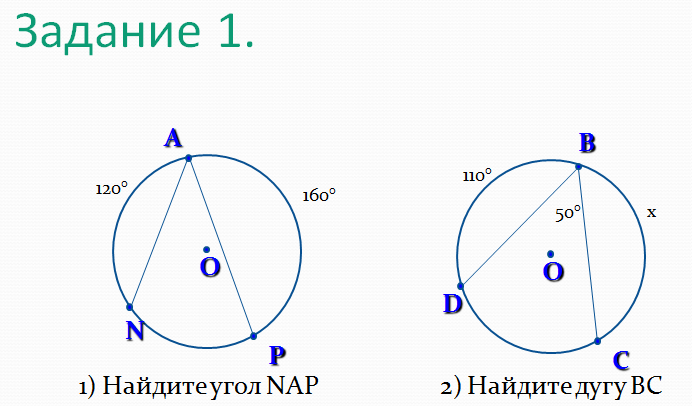
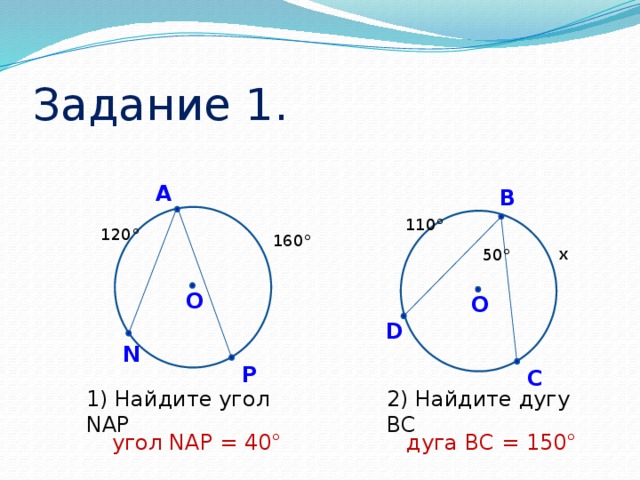
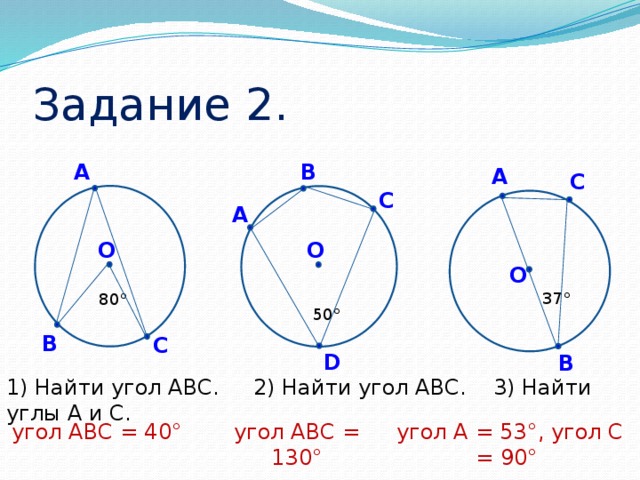
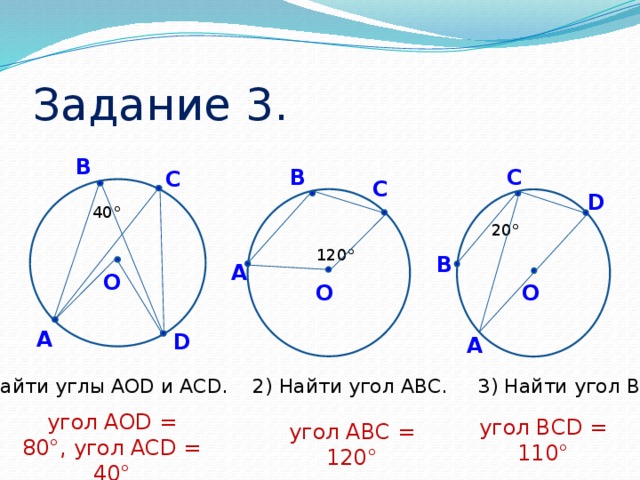
Задание 1 (самостоятельно, взаимопроверка) (Слайд № 15)

*Возьмите раздаточный материал, найдите задание №1. Посмотрите, какая задача поставлена перед вами. (Приложение 1)

*Задание выполняем на раздаточном материале.

*Проверяем

*Подведите итоги, поставьте в маршрутный лист баллы. (за каждый правильный 1 балл)

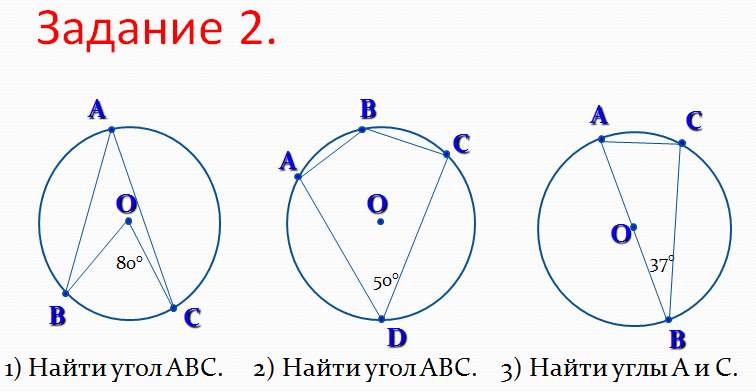
Задание 2 (в парах, самопроверка) (Слайд № 16)

Задание 3 (в группах, самопроверка) (Слайд № 17)

Задание 4 (запись в тетрадях и на доске)

(учебник стр 174 № 660) (Слайд № 18)

IV «Готовимся к ОГЭ»

Задачи этапа: проверить на основе сопоставления с эталоном свое умение применять теоретический материал при решении задач (ОГЭ).

Всем вам предстоит в скором будущем сдавать экзамен. В модуле «Геометрия» встречаются задачи на вписанные и центральные углы.

*Возьмите раздаточный материал «Готовимся к ОГЭ» (Приложение 2)

*Задание выполняем на раздаточном материале.

*Проверяем (самопроверка, на карточках)

*Подведите итоги, поставьте в маршрутный лист баллы. (2 задания оцениваем в общий балл, за решение более двух заданий дополнительная оценка).

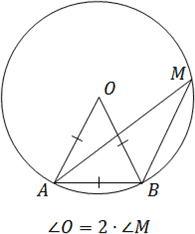
Задача №1.

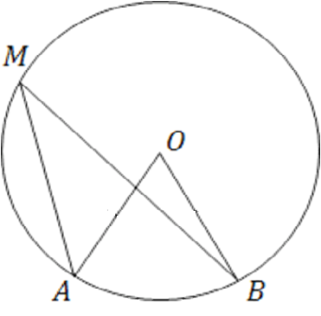
Точка О – центр окружности, угол АМВ =25⁰. Найдите величину угла AOB.

Задача №2.

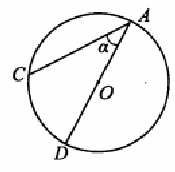
Найдите величину вписанного угла, опирающегося на дугу CD, величина которой равна 5/18 дуги всей окружности.

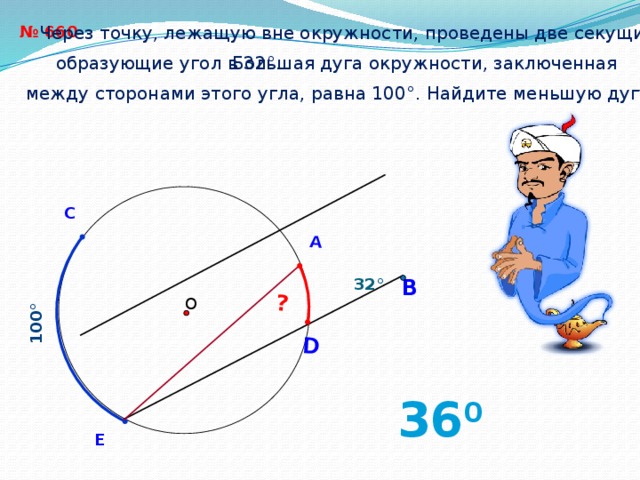
Задача №3.

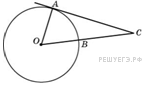Найдите угол АСО, если его сторона АС касается окружности, О – центр окружности, а меньшая дуга окружности АВ, заключенная внутри этого угла, равна 64 . Ответ дайте в градусах.

Задача №4.

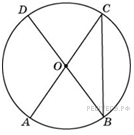В окружности с центром О  ,АС  и ВД – диаметры. Центральный угол АОД равен 110. Найдите вписанный угол АСВ. Ответ дайте в градусах.

Задача № 5

Найдите острый вписанный угол, опирающийся на хорду, равную радиусу окружности.

Задача №6

Центральный угол на 36° больше вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол.

Задача 7 (Слайд № 19)

Укажите номера верных утверждений:

1. Вписанный угол, опирающийся на диаметр, прямой.

2. Вписанным называется угол, вершина которого лежит в окружности.

3. Вписанный угол измеряется величиной дуги, на которую он опирается.

4. Центральным называется угол, вершина которого лежит в центре окружности.

5. Вписанный и центральный углы, опирающиеся на одну и ту же дугу равны.

 V Рефлексия. (Слайд № 20)

Задачи этапа: оценить собственную деятельность на уроке; зафиксировать неразрешенные затруднения как направления будущей учебной деятельности.

- Ребята, теперь посмотрим, как мы с вами потрудились.

-Справились с задачами, которые ставили на уроке?

Ответы: после теоретического повторения мы решали устные задачи, связанные с градусной мерой дуги, градусной мерой центрального угла; решали задачи на связь градусной меры центрального и вписанного угла, на применение следствий вписанного угла; применяли знания при решении задач из ОГЭ.

- Посчитайте свои баллы. Поднимите руки те, кто за урок получает «5», «4», «3».

Выставление оценок. (работают с листом самоконтроля)

VI. Домашнее задание (Слайд № 21)

- № 662

- Творческое задание «Эрудит» (составить кроссворд на тему «Вписанные и центральные углы»)

- Вы разработчики ОГЭ по математике. Вам необходимо составить задачу по теме «Центральные и вписанные углы».

Сдайте листы самооценки вместе с карточками.

Всем спасибо за урок. До свидания.

Приложение 1

Приложение 2

«Готовимся к ОГЭ»

Задача №1.

Точка О – центр окружности, угол АМВ =25⁰. Найдите величину угла AOB.

Задача №2.

Найдите величину вписанного угла, опирающегося на дугу CD, величина которой равна 5/18 дуги всей окружности.

Задача №3.

Найдите угол АСО, если его сторона АС касается окружности, О – центр окружности, а меньшая дуга окружности АВ, заключенная внутри этого угла, равна 64 . Ответ дайте в градусах.

Задача №4.

В окружности с центром О  ,АС  и ВД – диаметры. Центральный угол АОД равен 110. Найдите вписанный угол АСВ. Ответ дайте в градусах.

Задача № 5

Найдите острый вписанный угол, опирающийся на хорду, равную радиусу окружности.

Задача №6

Центральный угол на 36° больше вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол.

Задача №1.

Точка О – центр окружности, угол АМВ =25⁰. Найдите величину угла AOB.

Решение.

АМВ = 25 - вписанный угол, опирается на ᴗ АВ, = ᴗ АВ = 50.

АОВ – центральный угол, опирается на ᴗ АВ,= АОВ = 50.

Ответ: АОВ = 50.

_______________________________________________________________________

Задача №1.

Точка О – центр окружности, угол АМВ =25⁰. Найдите величину угла AOB.

Решение.

АМВ = 25 - вписанный угол, опирается на ᴗ АВ, = ᴗ АВ = 50.

АОВ – центральный угол, опирается на ᴗ АВ,= АОВ = 50.

Ответ: АОВ = 50.

__________________________________________________________

Задача №1.

Точка О – центр окружности, угол АМВ =25⁰. Найдите величину угла AOB.

Решение.

АМВ = 25 - вписанный угол, опирается на ᴗ АВ, = ᴗ АВ = 50.

АОВ – центральный угол, опирается на ᴗ АВ,= АОВ = 50.

Ответ: АОВ = 50.

Задача №2.

Найдите величину вписанного угла, опирающегося на дугу CD, величина которой равна 5/18 дуги всей окружности.

Решение.

Градусная мера окружности- 360; 360: 18*5 = 100 - дуга СD;

САD - вписанный угол, опирается на ᴗ СD, =  САD = 50 (по свойству)

Ответ: САD = 50.

______________________________________________________

Задача №2.

Найдите величину вписанного угла, опирающегося на дугу CD, величина которой равна 5/18 дуги всей окружности.

Решение.

Градусная мера окружности- 360; 360: 18*5 = 100 - дуга СD;

САD - вписанный угол, опирается на ᴗ СD, =  САD = 50

Ответ: САD = 50.

________________________________________________________

Задача №2.

Найдите величину вписанного угла, опирающегося на дугу CD, величина которой равна 5/18 дуги всей окружности.

Решение.

Градусная мера окружности- 360; 360: 18*5 = 100 - дуга СD;

САD - вписанный угол, опирается на ᴗ СD, =  САD = 50

Ответ: САD = 50.

Задача №3.

Найдите угол АСО, если его сторона АС касается окружности, О – центр окружности, а меньшая дуга окружности АВ, заключенная внутри этого угла, равна 64 . Ответ дайте в градусах.

Решение.

АС – касательная к окружности, =  ОАС = 90 (по свойству);

АОВ – центральный угол, опирается на ᴗ АВ,= АОВ = 64;

ΔАОС – прямоугольный треугольник ,= АСО = 90- 64 = 26.

Ответ: АСО = 26.

__________________________________________________________

Задача №3.

Найдите угол АСО, если его сторона АС касается окружности, О – центр окружности, а меньшая дуга окружности АВ, заключенная внутри этого угла, равна 64 . Ответ дайте в градусах.

Решение.

АС – касательная к окружности, =  ОАС = 90 (по свойству);

АОВ – центральный угол, опирается на ᴗ АВ,= АОВ = 64;

ΔАОС – прямоугольный треугольник ,= АСО = 90- 64 = 26.

Ответ: АСО = 26.

__________________________________________________________

Задача №3.

Найдите угол АСО, если его сторона АС касается окружности, О – центр окружности, а меньшая дуга окружности АВ, заключенная внутри этого угла, равна 64 . Ответ дайте в градусах.

Решение.

АС – касательная к окружности, =  ОАС = 90 (по свойству);

АОВ – центральный угол, опирается на ᴗ АВ,= АОВ = 64;

ΔАОС – прямоугольный треугольник ,= АСО = 90- 64 = 26.

Ответ: АСО = 26.

Задача №4.

В окружности с центром О, АС  и ВД – диаметры. Центральный угол АОД равен 110. Найдите вписанный угол АСВ. Ответ дайте в градусах.

Решение.

 АОD = 110 - центральный, опирается на ᴗ АD, = ᴗ АD = 110;

ВD – диаметр ,= ᴗ DАВ = 180, = ᴗ АВ = 180 - 110 = 70;

АСВ – вписанный, опирается на ᴗ АВ = 70, = АСВ = 35(по св)

Ответ: АСВ = 35

_________________________________________________________

Задача №4.

В окружности с центром О, АС  и ВД – диаметры. Центральный угол АОД равен 110. Найдите вписанный угол АСВ. Ответ дайте в градусах.

Решение.

 АОD = 110 - центральный, опирается на ᴗ АD, = ᴗ АD = 110;

ВD – диаметр ,= ᴗ DАВ = 180, = ᴗ АВ = 180 - 110 = 70;

АСВ – вписанный, опирается на ᴗ АВ = 70, = АСВ = 35(по св)

Ответ: АСВ = 35

_______________________________________________________

Задача №4.

В окружности с центром О, АС  и ВД – диаметры. Центральный угол АОД равен 110. Найдите вписанный угол АСВ. Ответ дайте в градусах.

Решение.

 АОD = 110 - центральный, опирается на ᴗ АD, = ᴗ АD = 110;

ВD – диаметр ,= ᴗ DАВ = 180, = ᴗ АВ = 180 - 110 = 70;

АСВ – вписанный, опирается на ᴗ АВ = 70, = АСВ = 35(по св)

Ответ: АСВ = 35

Задача № 5

Найдите острый вписанный угол, опирающийся на хорду, равную радиусу окружности.

  Решение.

АВ – хорда, АВ = r, ΔАВС- равносторонний. А =О = В = 60;

АОВ – центральный угол, опирается на ᴗ АВ,= ᴗ АВ = 60;

АМВ – вписанный, опирается на ᴗ АВ = 60, = АМВ = 30.

Ответ: АМВ = 30

________________________________________________________

Задача № 5

Найдите острый вписанный угол, опирающийся на хорду, равную радиусу окружности.

  Решение.

АВ – хорда, АВ = r, ΔАВС- равносторонний. А =О = В = 60;

АОВ – центральный угол, опирается на ᴗ АВ,= ᴗ АВ = 60;

АМВ – вписанный, опирается на ᴗ АВ = 60, = АМВ = 30.

Ответ: АМВ = 30

_________________________________________________________

Задача № 5

Найдите острый вписанный угол, опирающийся на хорду, равную радиусу окружности.

  Решение.

АВ – хорда, АВ = r, ΔАВС- равносторонний. А =О = В = 60;

АОВ – центральный угол, опирается на ᴗ АВ,= ᴗ АВ = 60;

АМВ – вписанный, опирается на ᴗ АВ = 60, = АМВ = 30.

Ответ: АМВ = 30

Задача №6

Центральный угол на 36° больше вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол.

Решение.

АОВ – центральный, опирается на ᴗ АВ;

АСВ – вписанный, опирается на ᴗ АВ

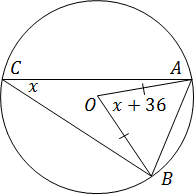
Пусть АСВ = х, тогда центральный АОВ = х+36. С другой стороны, центральный угол в 2 раза больше вписанного.

Значит  АОВ = 2АСВ, значит х+36=2х, х=36

Ответ: 36.

________________________________________________________

Задача №6

Центральный угол на 36° больше вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол.

Решение.

АОВ – центральный, опирается на ᴗ АВ;

АСВ – вписанный, опирается на ᴗ АВ

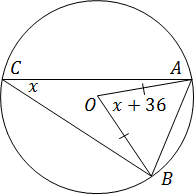
Пусть АСВ = х, тогда центральный АОВ = х+36. С другой стороны, центральный угол в 2 раза больше вписанного.

Значит  АОВ = 2АСВ, значит х+36=2х, х=36

Ответ: 36.

Лист самооценки ...........................................................

17

Краснова Т.Н., учитель математики,

БОУ «Мартюшевская СОШ»

Центральные

8 класс

и вписанные углы

Решение задач

Л.С. Атанасян Геометрия 7-9

• Как сформулируем цель урока?

Цель : отработать навыки решения задач на применение понятий вписанного и центрального углов, на применение теоремы о вписанном угле и её следствий.

Задачи:

• Повторить теоретический материал;
• Решать задачи на нахождение градусной меры угла, дуги;
• Решать задачи из ОГЭ;
• Выполним тест.

На какие группы вы бы разделили углы?

1

2

3

6

4

5

Вопросы

• Какой угол называется центральным?
• Каким соотношением связаны центральный угол и дуга, на которую он опирается?
• Дайте определение вписанного угла.
• Свойство вписанного угла.

Взаимооценка

Центральный угол

Это угол с вершиной в центре окружности.

О

Вписанный угол

Это угол, вершина которого лежит на окружности, а стороны пересекают окружность.

А

С

В

Найдите Х

№ 1

300 

60 

О

x

Найдите Х

№ 2

90 

О

x

45 

Найдите Х

№ 3

150 

x

30 

О

Найдите Х

№ 4

150 

Х

О

75 

Найдите Х

№ 5

90 

Х

О

Найдите Х

В

30 

№ 6

30 

D

А

Х

О

С

Решение

задач

Задание 1.

А

В

110°

120°

160°

x

50°

О

О

D

N

P

С

1) Найдите угол NAP

2) Найдите дугу ВС

угол NAP = 40°

дуга ВС = 150°

Задание 2.

B

А

А

C

C

А

О

О

О

37°

80°

50°

B

C

D

B

1) Найти угол АВС. 2) Найти угол АВС. 3) Найти углы А и С.

угол АВС = 40°

угол АВС = 130°

угол А = 53°, угол С = 90°

Задание 3.

B

C

B

C

C

D

40°

20°

120°

B

A

О

О

О

A

D

A

1) Найти углы АОD и ACD. 2) Найти угол АВС. 3) Найти угол ВСD.

угол АОD = 80°, угол ACD = 40°

угол ВСD = 110°

угол АВС = 120°

100 °

D

?

А

№ 660

Через точку, лежащую вне окружности, проведены две секущие,

Большая дуга окружности, заключенная

образующие угол в 32 °.

между сторонами этого угла, равна 100 °. Найдите меньшую дугу.

С

32 °

В

О

36 0

E

Укажите номера верных утверждений:

• Вписанный угол, опирающийся на диаметр, прямой.
• Вписанным называется угол, вершина которого лежит в окружности.
• Вписанный угол измеряется величиной дуги, на которую он опирается.
• Центральным называется угол, вершина которого лежит в центре окружности.
• Вписанный и центральный углы, опирающиеся на одну и ту же дугу равны.

Задачи:

• Повторить теоретический материал;
• Решать задачи на нахождение градусной меры угла, дуги;
• Решать задачи из ОГЭ;
• Выполним тест.

Домашнее задание.

• п. 70-71; № 662.

• Творческое задание «Эрудит»
• 1) Составить кроссворд на тему «Вписанные и центральные углы»
• 2) Составить задачу по теме «Центральные и вписанные углы»

Спасибо за урок.

До скорой встречи в увлекательном мире математики.