| ФИО педагога: | Ахметгареева А.А. | |
| Дата: |
| |
| Класс: 9 | Количество присутствующих: | Количество отсутствующих: |
| Раздел: | 9.3А Тригонометрия | |
| Тема урока: | Тригонометрические функции и их свойства | |
| Цели обучения в соответствии | 9.2.4.6 объяснять с помощью единичной окружности чётность (нечётность), периодичность, монотонность и промежутки знакопостоянства тригонометрических функций | |
| Цели урока | объясняет с помощью единичной окружности чётность (нечётность), периодичность тригонометрических функций | |
Ход урока
| Этап урока/ Время | Действия педагога | Действия ученика | Оценивание | Ресурсы |
| Начало урока 3 мин | 1.Организационный момент Приветствует учащихся, проверяет готовность к уроку, желает успеха. 2.ЭМН Проводит аутотренинг «Я знаю! Я умею! Я решу!» | Готовится к уроку, настраивается на совместную плодотворную деятельность, участвует в аутотренинге |
|
|
| 3. Озвучивание темы урока. Целеполагание. Учитель объявляет тему урока и цели обучения. Совместно с учащимися формулируются цели урока. Далее учитель озвучивает критерии оценивания. Критерии оценивания: объяснять с помощью единичной окружности четность (нечетность), периодичность тригонометрических функций; использовать свойства четности, периодичности тригонометрических функций при решении заданий. | Узнает тему урока, участвует в постановке цели урока, определяет для себя критерии оценивания.
| Словесная оценка учителя |
| |
| Середина урока 33 мин.
| 4. Актуализация знаний. 1) Мозговой штурм. - Какие функции называются тригонометрическими? - Чему равно значение sin300? - Чему равно значение cos600? - Чему равно значение tg900? - Чему равно значение ctg 450? - Какая окружность называется единичной? - В какой четверти находится угол равный 1500? - В какой четверти находится угол равный -2780? - В какой четверти находится угол равный 3860? Используя свойства четности тригонометрических функций, найти значения выражения: sin(-100); tg(-200); cos(-450); сtg(-500).
| Отвечает на поставленные вопросы, участвует в обсуждении. Выполняет формативные задания, осуществляет самооценивание Проводит коррекцию знаний. | Словесная оценка учителя. Самооценивание
| Дидактический материал
|
| 5. Закрепление изученного материала. 1) Четность тригонометрических функций.
Пример1. Используя свойства четности тригонометрических функций, найти значения выражения: sin(-200); tg(-600); cos(-450); сtg(-300). Решение: sin(-200)= cos(-450)= cos450= сtg(-300)=
Вычислить: 1) Решение: 1) 2)
|
Коллективная работа
Выполняют предложенные задания
Записывает примеры в тетрадь
Индивидуальная работа | Словесная оценка учителя.
Обратная связь
ФО |
прилож | |
| Конец урока 4 мин. | 6. Итог урока – Какую цель мы ставили в начале урока? – Проанализируйте свою работу на уроке. - В чем было затруднение? Что осталось непонятным? | Подводит итог урока, анализирует свою деятельность на уроке, определяет достижение поставленных целей. |
|
|
| 7.Постановка домашнего задания | Записывают д/з |
| дневник. | |
| 8.Рефлексия «Рефлексивный ринг» Я научился… У меня получилось… Было трудно… Я смог … Я понял, что… | Высказывают свое мнение о уроке. |
|
|

 Получите свидетельство
Получите свидетельство Вход
Вход



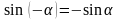 ;
; 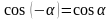 ;
; 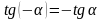 ;
; 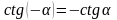 .
. 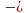 sin200; tg(-600)=
sin200; tg(-600)= 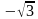 ;
;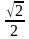 ;
; 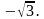
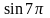 ; 2)
; 2) 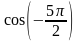
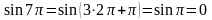 .
.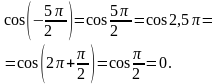









 Тригонометрические функции и их свойства. Краткосрочное планирование. (63.7 KB)
Тригонометрические функции и их свойства. Краткосрочное планирование. (63.7 KB)
 0
0 257
257 16
16 Нравится
0
Нравится
0


