Тригонометрическая и показательная форма комплексного числа

Тригонометрическая форма комплексного числа

Геометрическое изображение комплексных чисел

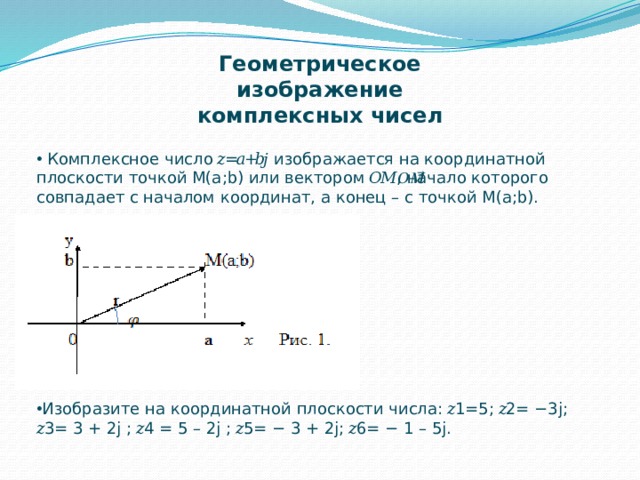
• Комплексное число 𝑧=𝑎+𝑏𝑗 изображается на координатной плоскости точкой М(a;b) или вектором 𝑂𝑀⃗, начало которого совпадает с началом координат, а конец – с точкой М(a;b).

• Изобразите на координатной плоскости числа: 𝑧1=5; 𝑧2= −3j;

𝑧 3= 3 + 2j ; 𝑧4 = 5 – 2j ; 𝑧5= − 3 + 2j; 𝑧6= − 1 – 5j.

Модуль и аргумент комплексного числа

• Определение . Модулем комплексного числа называется абсолютная величина вектора, соответствующего этому числу.

Модуль числа z = a + bj обозначается |𝑧| или |𝑎+𝑏𝑗| или r.

На основании теоремы Пифагора (см. рис.1) получается формула

• Например, комплексное число z = 8 − 6 j имеет модуль равный 10, так как |𝑧|=√82+(−6)2=√64+36=√100=10.

Определение. Аргументом комплексного числа 𝑧≠0 называется величина угла между положительным направлением оси Оx и вектором, соответствующим этому числу (см. рис. 1).

Аргумент обозначается 𝜑, arg z или arg (𝑎+𝑏 𝑗).

Аргумент комплексного числа 𝑧=𝑎+𝑏𝑗 определяется неоднозначно , т.е. одному комплексному числу соответствует бесконечное множество аргументов.

Правило нахождения аргумента комплексного числа

1. Найти tg 𝜶 =|𝒃𝒂|.

2. Найти 𝜶=arctg|𝒃𝒂|.

3. Выяснив, в какой четверти лежит вектор, соответствующий числу, найти аргумент 𝝋.

Если 𝝋 ∈ 1 четверти, то 𝝋 = 𝜶

𝝋 ∈ 2 четверти, то 𝝋=𝟏𝟖𝟎- 𝜶

𝝋 ∈ 3 четверти, то 𝝋=𝟏𝟖𝟎+ 𝜶

𝝋 ∈ 4 четверти, то 𝝋 = 𝟑𝟔𝟎- 𝜶

Примеры:

Найти модуль и аргумент комплексного числа.

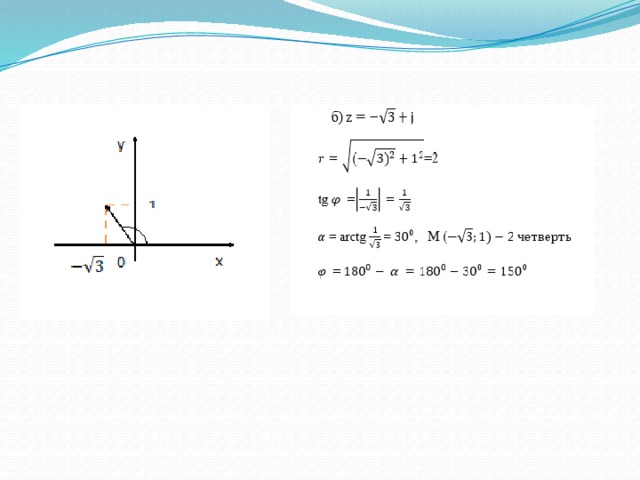
Тригонометрическая форма комплексного числа

Пусть дано комплексное число 𝑧=𝑎+𝑏𝑗. Из ∆ ОМА можно выразить действительные числа а и b через модуль r и аргумент 𝜑 числа z следующим образом: 𝑎=𝑟cos𝜑,𝑏=𝑟sin𝜑.

Таким образом, комплексное число можно записать в виде 𝑧=𝑟(cos𝜑+j sin𝜑), где r – модуль комплексного числа, 𝜑 - один из его аргументов.

Представление комплексного числа z в виде z = r (𝐜𝐨𝐬𝝋+𝐣 𝐬𝐢𝐧𝝋) называется тригонометрической формой записи комплексного числа.

Правило перехода от алгебраической формы записи

комплексного числа к тригонометрической

Для того чтобы перейти от алгебраической формы записи к тригонометрической нужно :

1. Найти модуль комплексного числа по формуле: r=√𝒂𝟐+𝒃𝟐

2. Найти один из аргументов комплексного числа, пользуясь правилом нахождения аргумента.

3. Записать комплексное число в тригонометрической форме .

Примечание

Модули и аргументы действительных чисел и чисто мнимых чисел надо находить непосредственно исходя из их геометрического изображения, а не используя приведенное выше правило (тем более, что для чисто мнимых чисел это правило вообще нельзя применять).

Чтобы перейти от тригонометрической формы записи обратно к алгебраической форме нужно найти значения sin𝜑 и cos𝜑 при данном аргументе и умножить на модуль .

Например: 𝑧=3(cos120°+𝑗sin120°)=3∗(−12+√32𝑗)=−32+3√32𝑗

1. Умножение

2. Деление

3. Возведение в степень

4. Извлечение корня из комплексного числа .

Изобразить на координатной плоскости числа:

1. 𝑧 = 5; 4. z = 5 – 2j; 7. 𝑧=3(cos40°+𝑗sin40°)

2. 𝑧 = −3𝑗; 5. Z = − 3 + 2j; 8. 𝑧=5(cos120°+𝑗sin120°)

3. z = 3 + 2j; 6. z = − 1 – 5j. 9. 𝑧=2(cos330°+𝑗sin330°)

Записать в тригонометрической форме комплексные числа:

10. 𝑧=1+𝑗. 11. 𝑧=−2+2𝑗. 12. 𝑧=√3+𝑗. 60. 𝑧=−3+3𝑗.

13. 𝑧=2√2−2𝑗√6; 14. 𝑧=− √3𝑗. 15. 𝑧=−10. 64. 𝑧=6𝑗.