Получите свидетельство
Вход
Треугольники и их элементы
1. 
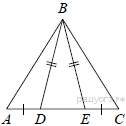На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.
2. Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1 равны.
3. В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1CB1 и ACB подобны.
4. В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.
5. Окружности с центрами в точках E и F пересекаются в точках C и D, причём точки E и F лежат по одну сторону от прямой CD. Докажите, что CD ⊥ EF.
6. Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1 равны.
7. 
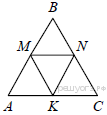В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
8. На стороне 
треугольника 
отмечены точки 
и 
так, что 
. Докажите, что если 
, то 
.
9. На медиане 
треугольника 
отмечена точка . Докажите, что если 
, то 
.
10. Докажите, что биссектрисы углов при основании равнобедренного треугольника равны.
11. Два равносторонних треугольника имеют общую вершину. Докажите, что отмеченные на рисунке отрезки 
и 
равны.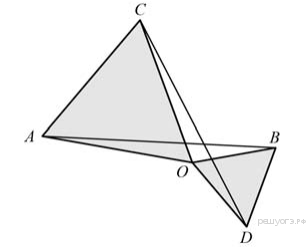
12. Два равных прямоугольника имеют общую вершину 
(см. рис.). Докажите, что площади треугольников 
и 
равны.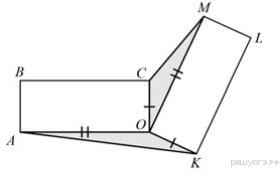
13. В параллелограмме 
проведены высоты 
и 
. Докажите, что 
подобен .
14. Докажите, что у равных треугольников и биссектрисы, проведённые из вершины 
и 
, равны.
15. В треугольнике угол 
равен 36°, — биссектриса. Докажите, что треугольник 
— равнобедренный.
16. В остроугольном треугольнике ABC угол B равен 60°. Докажите, что точки A, C, центр описанной окружности треугольника ABC и точка пересечения высот треугольника ABC лежат на одной окружности.
17. Окружность касается стороны AB треугольника ABC, у которого ∠C = 90°, и продолжений его сторон AC и BC за точки A и B соответственно. Докажите, что периметр треугольника ABC равен диаметру этой окружности.
18. На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
19. На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
20. В остроугольном треугольнике ABC точки A, C, центр описанной окружности O и центр вписанной окружности I лежат на одной окружности. Докажите, что угол ABC равен 60°.
21. В остроугольном треугольнике ABC угол B равен 60° . Докажите, что точки A, C, центр описанной окружности треугольника ABC и центр вписанной окружности треугольника ABC лежат на одной окружности.
22. Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке K. Докажите, что треугольники KAB и KCD подобны.
23. Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.
24. В треугольнике ABC с тупым углом ACB проведены высоты AA1 и BB1. Докажите, что треугольники A1CB1 и ACB подобны.
25. Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке K. Докажите, что треугольники KAB и KCD подобны.
26. В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.
27. В треугольнике ABC с тупым углом BAC проведены высоты BB1 и CC1. Докажите, что треугольники AB1C1 и ABC подобны.
28. В треугольнике на его медиане 
отмечена точка 
так, что . Найдите отношение площади треугольника к площади треугольника
29. В остроугольном треугольнике проведены высоты 
и 
. Докажите, что углы 
и 
равны.
Треугольники и их элементы (задание № 24) (133.88 KB)
0
1135
52
Нравится
0
