Тренировочный вариант к экзамену по математике в 9 классе

ВАРИАНТ 1 Часть 1

Модуль «Алгебра»

№1Найдите значение выражения .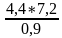

№2В таблице даны результаты забега мальчиков 8 класса на дистанцию 60 м. Зачёт выставляется при условии, что показан результат не хуже 10,5 с.

Укажите номера дорожек, по которым бежали мальчики, получившие зачёт.

1) только I 2) только II 3) I, IV 4) II, III

№3 Между какими числами заключено число ?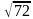

1) 24 и 26 2) 8 и 9 3) 71 и 73 4) 4 и 5

№4Какое из данных ниже чисел является значением выражения ?

1) 8 2) 1024 3) - 8 4)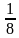

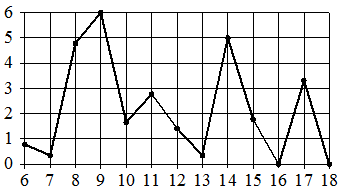№ 5 На рисунке жирными точками показано суточное количество осадков, выпадавших в Петрозаводске с 6 по 18 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода в Петрозаводске не выпадало осадков.

№6 Найдите корень уравнения (x−5)² =(x+10)².

№7 Товар на распродаже уценили на 20%, при этом он стал стоить 940 рублей. Сколько рублей стоил товар до распродажи?

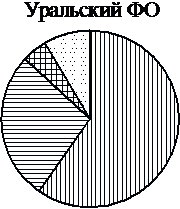
№ 8 На диаграмме показано распределение земель Уральского федерального округа по категориям. Определите по диаграмме, земли каких категорий занимают более 25% площади округа.

*Прочие земли — это земли поселений; земли промышленности и иного специального назначения; земли особо охраняемых территорий и объектов

1) Земли лесного фонда 2) Земли сельскохозяйственного назначения

3) Земли запаса 4) Прочие земли

В ответ запишите номера выбранных вариантов ответов без пробелов, запятых и других дополнительных символов.

№9 Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,2. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.

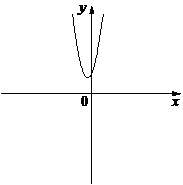
№10 На рисунках изображены графики функций вида y=ax²+bx+c. Установите соответствие между знаками коэффициентов a и c и графиками функций.

КОЭФФИЦИЕНТЫ А) a0 Б) a0, c0 В) a0, c

ГРАФИКИ

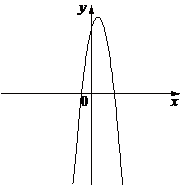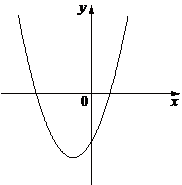1) 2) 3)

В таблице под каждой буквой укажите соответствующий номер.

№11 Геометрическая прогрессия (b_n) задана условиями: b₁=−7, b_n+1=3b_n.

Найдите сумму первых пяти её членов.

№12 Найдите значение выражения 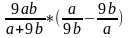при a = 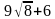, b =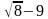

№13 Центростремительное ускорение при движении по окружности (в м/​с²) вычисляется по формуле a=ω²R, где ω — угловая скорость (в с⁻¹),

R — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 0,5с⁻¹, а центростремительное ускорение равно 2,25м/​с². Ответ дайте в метрах.

№14Укажите неравенство, решением которого является любое число.

1) x²−560 2) x²+560

3) x²−56²+56

Модуль «Геометрия»

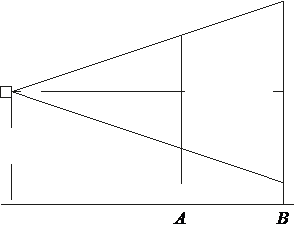№ 15 Проектор полностью освещает экран A высотой 140 см, расположенный на расстоянии 210 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 380 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.

№ 16 Катеты прямоугольного треугольника равны 18 и 24. Найдите высоту, проведённую к гипотенузе.

№17 Периметр треугольника равен 50, одна из сторон равна 20, а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.

№ 18 Найдите площадь параллелограмма, изображённого на рисунке.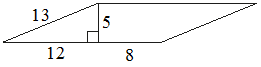

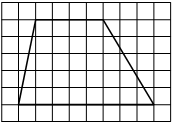
№19 На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

№20 Какое из следующих утверждений верно?

1) Площадь трапеции равна произведению основания трапеции на высоту.

2) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.

3) Существует прямоугольник, диагонали которого взаимно перпендикулярны.

В ответ запишите номер выбранного утверждения.