Типы дополнительных построений в треугольнике при решении задач

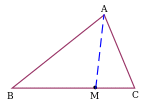
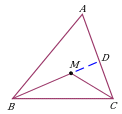
Проведение отрезка, соединяющего вершину треугольника с некоторой точкой на противоположной стороне.

Дополнительное построение позволяет воспользоваться неравенством треугольника для ∆ABM и ∆ACM.

Частные случаи дополнительных построений I типа

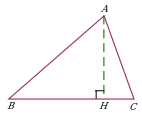
Проведение высоты в произвольном треугольнике.

Дополнительное построение позволяет использовать:

1. тригонометрические функции острых углов прямоугольного треугольника;

2. свойства наклонных.

См. задачу 1

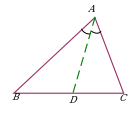
Проведение биссектрисы, высоты, медианы в равнобедренном треугольнике.

Дополнительное построение позволяет использовать равенство треугольников ∆ABD и ∆ACD.

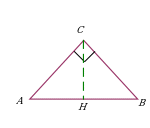
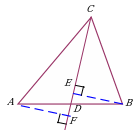
Проведение высоты в прямоугольном треугольнике.

Данное дополнительное построение позволяет использовать:

1. подобие треугольников ∆ABC и ∆ACH; ∆ABC и ∆CBH; ∆ACH и ∆CBH, и в частности, свойства средних пропорциональных отрезков в прямоугольном треугольнике ∆ABC;

2. теорему Пифагора.

Проведение биссектрисы в произвольном треугольнике

Данное дополнительное построение позволяет использовать свойства биссектрисы треугольника ∆ABC.

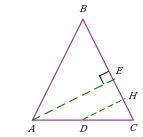
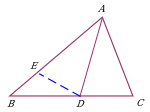
Проведение высоты к боковой стороне в равнобедренном треугольнике.

Дополнительное построение позволяет воспользоваться подобием треугольников ∆AEC и ∆DHC, где DH – средняя линия треугольника ∆AEC.

См задачу 2

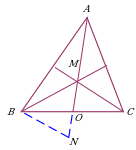
Удвоение отрезка.

Дополнительное построение позволяет рассмотреть свойства треугольника ∆BMN, стороны которого равны двум третям медиан треугольника ∆ABC.

Частные случаи дополнительных построений II типа.

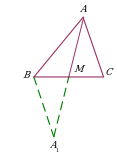
Удвоение медианы.

Дополнительное построение позволяет использовать равенство треугольников ∆AMC и ∆A₁MB.

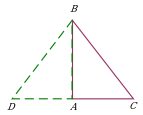
Удвоение катета прямоугольного треугольника.

Дополнительное построение позволяет использовать свойства равнобедренного треугольника ∆BCD.

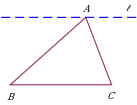
Проведение прямой, параллельной противолежащей стороне.

Дополнительное построение позволяет использовать свойства углов при параллельных прямых и BC и секущей AB.

См.

- теорему о сумме внутренних углов треугольника

- теорему о пересечении высот треугольника

- задачу 3

Частные случаи дополнительных построений III типа.

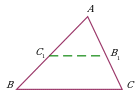
Проведение прямой через точку в треугольнике, параллельной одной из сторон.

Дополнительное построение позволяет использовать подобие треугольников ∆ABC и ∆AC₁B₁.

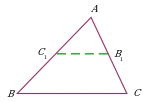
Проведение средней линии треугольника.

Дополнительное построение позволяет использовать:

1. свойства средней линии треугольника;

2. подобие треугольников ∆ABC и ∆AC₁B₁.

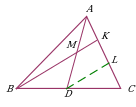
Проведение параллельной прямой до пересечения со стороной в точке.

Дополнительное построение позволяет использовать подобные треугольники ∆AKM и ∆ALD.

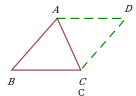
Проведение прямых, параллельных сторонам треугольника.

Дополнительное построение позволяет использовать:

1. равенство треугольников ∆ABC и ∆ADC;

2. равенство площадей треугольников ∆ABC и ∆ADC.

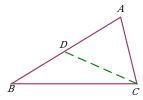
Откладывание отрезка, равного данному.

Дополнительное построение позволяет использовать:

1. равенство треугольников ∆ADE и ∆ADC;

2. свойство внешнего угла AED треугольника ∆BDE.

Частные случаи дополнительных построений IV типа.

Откладывание отрезка, равного меньшей стороне.

Дополнительное построение позволяет использовать:

свойства равнобедренного треугольника ∆ACD.

V тип дополнительных построений: на продолжении одной из сторон треугольника отложить отрезок, равный другой стороне.

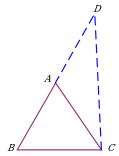
На продолжении одной из сторон треугольника отложить отрезок, равный другой стороне.

Дополнительное построение позволяет использовать:

1) свойство равнобедренного треугольника ∆ADC;

2) свойство внешнего угла BAC треугольника ∆ACD.

Продолжение отрезка до пересечения со стороной.

Дополнительное построение позволяет использовать неравенство треугольника.

VII тип дополнительных построений: проведение прямой через данную точку перпендикулярно данной прямой.

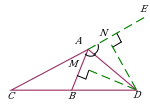
Проведение прямой через данную точку перпендикулярно данной прямой.

Дополнительное построение позволяет рассматривать подобные треугольники ∆ADF и ∆BDE.

Частные случаи дополнительных построений VII типа.

На стороны треугольника опустить перпендикулярные прямые.

Дополнительное построение позволяет воспользоваться свойством биссектрисы угла.

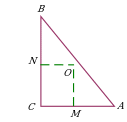
Провести прямые, перпендикулярные катетам прямоугольного треугольника.