Конспект урока по математике
Преподаватель Дмитрива В.М.
Тема: Арифметические операции над функциями. Сложная функция (композиция). Понятие о непрерывности функции. Обратные функции. Область определения и область значений обратной функции. График обратной функции.
Цели:
образовательная: Ввести понятия: Арифметические операции над функциями. Сложная функция (композиция). Понятие о непрерывности функции. Обратные функции. Область определения и область значений обратной функции. График обратной функции.
развивающая: продолжить работу по развитию наблюдательности, умения сравнивать делать вывод;
воспитательная: формирование у обучающихся самостоятельности, трудолюбия, прививать чувства ответственности и сознательного отношения к изучаемому материалу.
Тип урока: Комбинированный урок.
Метод проведения: Сочетания фронтальной и индивидуальной работы с обучающимися.
Оборудование урока: Учебник, проектор, ПК, презентация.
ХОД УРОКА
1. Орг. момент: Приветствие группы, проверка дежурства, состояние кабинета, наличие студентов, готовность к занятиям.
Проверка наличия и ведения конспектов, домашнего задания; опрос.
2. Сообщение темы урока, постановка цели и задачи: Актуализация и мотивация познавательной деятельности студентов.
— Предположим, что у вас в кармане два яблока. Некто взял у вас одно яблоко. Сколько у вас осталось яблок?
— Два.
— Подумайте хорошенько. Буратино сморщился, — так здорово подумал.
— Два…
— Почему?
— Я же не отдам Некту яблоко, хоть он дерись!
к/ф «Золотой ключик, или приключения Буратино»
Всем нам хорошо известны основные арифметические операции: сложение, вычитание, умножение и деление. Сначала мы складывали и вычитали яблоки. Потом целые числа. Затем перешли к изучению операций над числами дробными. И вот наконец то пришла очередь операций над функциями. Да да, не удивляйтесь, функции, как и обычные числа можно складывать и вычитать, умножать и делить.
3. Изучение нового материала: Лекция.
Определение: Суммой функций f(x) и g(x) называется функция (f+g)(x), которая для каждого x из множества X принимает значение f(x)+g(x).
(f+g)(x)=f(x)+g(x), D(f+g)=D(f)∩D(g).
Аналогично определяется произведение функций: (f⋅g)(x)=f(x)⋅g(x),
D(f⋅g)=D(f)∩D(g).
Разность функций: (f−g)(x)=f(x)−g(x), D(f−g)=D(f)∩D(g).
Частное функций: (f/g)(x)=f(x)/g(x), D(fg)=D(f)∩D(g)∖Mg, Mg={x∈D(g):g(x)=0}.
Разумеется определения операций над функциями как всегда просты и понятны, но если они вызывают у вас некоторое смущение, то вы можете обратиться к примерам.
Прочитав определение определение суммы функций, мы задаем себе вполне логичный вопрос: «А что все это значит?» Давайте же разберемся, как будет выглядеть сложение функций на практике.
Пример:
Пусть у нас есть функция f(x) = 1 +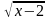 и функция g(x) = x — 1
и функция g(x) = x — 1
Тогда их сумма определяется как (f + g)(x) = f(x) + g(x) = (1 + 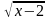 ) + (x — 1) = x +
) + (x — 1) = x + 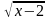
Как видите, здесь нет ничего сложного. Основные проблемы начинаются при нахождении область определения результирующей функции. Говоря простым языком, область определения суммы функций является пересечением (общей частью) областей определения исходных функций.
Для нашего примера:
| Функция | Область определения |
| f(x) = 1 + √x — 2 | [2; +∞) |
| g(x) = x — 1 | (-∞ +∞) |
| (f + g)(x) = x + √x — 2 | [2; ∞)∩(-∞ +∞) = [2; ∞) |
Рассмотрим более сложный вариант.
Возьмем две функции
f(x) = 3√x и g(x) = √x
Тогда их произведение определяется как
(f*g)(x) = f(x).g(x) = (3√x)(√x) = 3x
Казалось бы, для области определения результирующей функции (f*g)(x) = 3x нет никаких ограничений, но
| Функция | Область определения |
| f(x) = 3√x | [0; +∞) |
| g(x) = √x | [0; +∞) |
| (f.g)(x) = 3x, x ≥ 0 | [0; +∞) ∩ [0; +∞) = [0; +∞) |
И напоследок самое простое, давайте расшифруем строку из определения деления функций:
(f/g)(x)=f(x)/g(x), D(fg)=D(f)∩D(g)∖Mg, Mg={x∈D(g):g(x)=0}.
Включаем переводчик….
Translate: Для f/g, область определения есть пересечение областей определения функций f и g кроме точек, где g(x) = 0
f(x)=x+100500
g(x)=x*√2+x, тогда
g(x)=0 при x=-2 и x=0
| Функция | Область |
| f(x) = x+100500 | (-∞ +∞) |
| g(x) = x*√2+x | [-2; +∞) |
| (f/g)(x) = (x+100500)/(x*√2+x), | (-2; 0) ∩ (0; +∞) |
| Понятие о сложной функции |
| Пример. Функцию z = |
| Для записи композиции функций употребляется значок |
| Пример. z = |
| Взаимно обратные функции Пусть дана функция у = f(x). Она имеет обратную, если из зависимости у = f(x) можно переменную х однозначно выразить через переменную у. Выразив х через у, мы получим равенство вида х = g(y). В этой записи g обозначает функцию, обратную к f. Если функция g является обратной для функции f, то и функция является обратной для функции g. Пару функций f и g называют взаимно обратными функциями. |
| График обратной функции Если мы одновременно построим графики функций f и g в одной и той же системе координат, откладывая по оси абсцисс аргументы обеих функций, а по оси ординат – их значения, то эти графики будут симметричны друг другу относительно прямой у = х. |
| Свойства взаимно обратных функций Отметим некоторые свойства взаимно обратных функций. |
![]()
![]()
Примеры нахождения обратных функций:
1) y=3x-8
1. x=3y-8, 2. 3y=x+8, 3. y=(x+8)/3.
2) y=11-5x
1. x=11-5y, 2. 5y=11-x, 3. y=(11-x)/5.
4. Закрепление изученного материала: Комментированное решение у доски: 
5. Подведение итогов урока: Вывод о достижении цели занятия.
6. Домашнее задание.
О.2 п. 1.6. № 1.58 (а, в), 1.59 (б) стр. 30

 Получите свидетельство
Получите свидетельство Вход
Вход



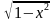 можно рассматривать как композицию функций y = 1 -
можно рассматривать как композицию функций y = 1 - 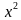 и z =
и z = 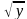 .
. g означает, что функция h получена как композиция функций f и g (сначала применяется g, а затем f), т. е. (f
g означает, что функция h получена как композиция функций f и g (сначала применяется g, а затем f), т. е. (f 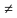 f
f 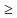 0, т. е. те, для которых число 1 -
0, т. е. те, для которых число 1 - 








 Тема: Арифметические операции над функциями. Сложная функция (композиция). Понятие о непрерывности функции. Обратные функции. Область определения и область значений обратной функции. График обратной функции. (167.99 KB)
Тема: Арифметические операции над функциями. Сложная функция (композиция). Понятие о непрерывности функции. Обратные функции. Область определения и область значений обратной функции. График обратной функции. (167.99 KB)
 0
0 2087
2087 160
160 Нравится
0
Нравится
0


