Тосненский район Ленинградская область
(Курсовая работа в рамках повышения квалификации)
Тема: «Текстовые задачи на совместную работу»
Выполнили:
Алексеева Наиля Хакимовна, учитель математики высшей квалификационной категории
МКОУ «Саблинская ООШ»,
Загуляева Надежда Георгиевна, учитель математики МКОУ «Ушакинская ООШ №2»,
Симанова Нина Алексеевна, учитель математики
МКОУ «Ушакинская ООШ №2»
2017 год
ВведениеЗадачи являются важнейшим средством формирования у школьников системы основных математических знаний, умений и навыков, ведущей формой учебной деятельности, одним из основных средств математического развития.
Функции задач разнообразны: обучающие, развивающие, воспитывающие, контролирующие. Они служат мотивом для введения новых понятий, средством для установления связей между понятиями, помогают учащимся овладеть математическим методом показания реального мира.
Каждая задача может служить многим конкретным целям обучения. И все же главная цель – развить творческое и математическое мышление учащихся, заинтересовать их математикой, привести к «Открытию» математических фактов. Умение решать задачи – это умение рассуждать. Оно требуется в повседневной жизни, при изучении различных учебных предметов. Для математического развития учащихся полезно одну задачу решить несколькими способами (если это возможно) и не жалеть на это времени. Затем из различных способов выбрать наиболее рациональный, красивый.
Объект исследования: подготовка учащихся к экзамену по математике в формате ОГЭ.
Предмет исследования: текстовые задачи на совместную работу.
Цель исследования: определить преемственность текстовых задач на совместную работу с 5 по 9 класс.
Задачи исследования:
выбрать текстовые задачи на совместную работу на разных уровнях обучения;
разработать цепочку подготовительных задач;
проанализировать наличие и решение таких задач в учебниках математики А.Г. Мерзляк, В.Б. Полонский, М.С. Якир – 5-6 классы, и учебниках алгебры Ю.Н.Макарычева 7-9 классы.
№ 1.1. один комбайнер намолотил 231т зерна, а второй – на 31т меньше. Сколько тонн зерна они намолотили вместе?
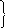

I – 231т
? т
II –?т, на 31т
231 – 31 = 200 (т) зерна намолотил II комбайнер.
231 + 200 = 431(т) зерна намолотили оба комбайнера вместе.
Ответ: 431т.
№ 1.2. Один тракторист вспахал 13,8га земли, что оказалось на 4,7га меньше, чем второй тракторист. Сколько га земли вспахали оба тракториста вместе?
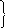
I – 13,8га, на 4,7га
? га

II –?га, на 31т
13,8 – 4,7 = 9,1 (га) земли вспахал первый тракторист.
13.8 + 9.1 = 22.9 (га) земли вспахали оба тракториста.
Ответ: 22,9га
№ 1.3. Один тракторист вспахал 5,6га земли, а другой в 2 раза больше. Сколько га земли они вспахали вместе?
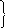

I – 5,6га
?га
II –?га, в 2р.
5,6 3 = 11,2 (га) вспахал второй тракторист.
5,6 + 11,2 = 16,8 (га) земли вспахали оба тракториста.
Ответ: 16,8га
№ 1.4. Два тракториста вспахали вместе 12,32га земли, причем один из них вспахал в 1,2 раза меньше другого. Сколько га земли вспахал каждый тракторист?
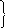
I – ?га, в 1,2 разага
12,32 га

II –?га
1 способ:
Пусть х га земли вспахал I тракторист.
Тогда 1,2х га – вспахал II тракторист.
(х + 1,2х) га – земли вспахали оба вместе, а это 12,32 га земли.
Составим и решим уравнение:
_123,2 22
110 5,6
_132
132
0
х + 1,2х = 12,32
2,2х = 12,32
х = 12,32 2,2
х = 123,2 22
х = 5,6
5,6га земли вспахал I тракторист.
2) 12,32 – 5,6 = 6,72 (га) земли вспахал II тракторист.
Ответ: 5,6га; 6,72га.
2 способ:
2) 5,6 1,2 = 6,72 (га) вспахал II тракторист.
Ответ: 5,6га; 6,72га.
№1.5. Три бригады изготовили вместе 114 деталей. Известно, что вторая бригада изготовила деталей в 3 раза больше., чем первая и на 16 деталей меньше, чем третья. На сколько деталей больше изготовила третья бригада, чем первая?

I - ? деталей
114 деталей
114 деталей
II - ? деталей, в 3 р. и на 16 деталей
III - ? деталей
Пусть х деталей изготовила I бригада, тогда
I – х деталей
II – 3х деталей
III – (3х + 16) деталей
Составим и решим уравнение
х + 3х + 3х + 16 = 114
7х = 98
х = 14
14 деталей изготовила первая бригада.
14 3 = 42 (дет.) изготовила вторая бригада
42 + 16 = 58 (дет.) изготовила третья бригада
58 – 14 = 44 (дет.)
Ответ: на 44 детали больше изготовила третья бригада, чем первая.
№ 1.6. Три бригады изготовили вместе 266 деталей. Известно, что вторая бригада изготовила деталей в 4 раза больше, чем первая и на 5 деталей меньше, чем третья. На сколько деталей больше изготовила третья бригада, чем первая?
№ 1.7. Три бригады вместе изготовили 114 карданных валов. Известно, что вторая бригада изготовила карданных валов в 3 раза больше, чем первая и на 15 карданных валов меньше, чем третья. На сколько карданных валов больше изготовила третья бригада, чем первая?
№ 1.8. Три бригады вместе изготовили 114 синхронизаторов передач. Известно, что вторая бригада изготовила синхронизаторов в 3 раза больше, чем первая и на 16 синхронизаторов меньше, чем третья. На сколько синхронизаторов передач больше изготовила третья бригада, чем первая?
№ 1.9. Три бригады изготовили вместе 248 деталей. Известно, что вторая бригада изготовила деталей в 4 раза больше, чем первая и на 5 деталей меньше, чем третья. На сколько деталей больше изготовила третья бригада, чем первая?
№ 2.1. Молодой рабочий изготавливает за 8 ч 144 детали, а его наставник за это же время изготавливает 192 детали. Какова производительность каждого рабочего?
|
| Всего деталей | Время в часах | Производительность в дет./ ч |
| Молодой рабочий | 144 | 8 | ? |
| Наставник | 192 | 8 | ? |
№ 2.2. Один рабочий изготовил 16 одинаковых деталей за 6ч, а другой 24 такие же детали за 15ч. Какой из них тратил на изготовление одной детали больше времени и на сколько?
|
| Всего деталей | Время в часах | Производительность в дет./ ч |
| I | 16 | 6 |
на ? |
| II | 24 | 15 |
|
№ 2.3. на изготовление 231 детали ученик тратит на 11 часов больше, чем мастер на изготовление 462 таких же деталей. Известно, что ученик за час делает на 4 детали меньше, чем мастер. Сколько деталей в час делает ученик?
|
| Всего деталей | Производительность в дет./ ч | Время в часах |
| Ученик | 231
| х |
на 11ч |
| Мастер | 462
| х + 4 | |
х дет. / ч - производительность ученика. (х 0)
Составим и решим уравнение:
-
= 11 х (х + 4)
231(х + 4) – 462х = 11х(х + 4)
231х + 924 – 462х = 11х2 + 44х
11х2 + 275х – 924 = 0 11
х2 + 25х -84 = 0
D = 625 – 4 1 (-84) = 961
= 31
Х1 = - не удовлетворяет условию х 0
Х2 =
3 детали в час делает ученик.
Ответ: 3 детали.
№ 2.4. Первый рабочий в час делает на 10 деталей больше, чем второй, и выполняет заказ, состоящий из 60 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
№ 2.5. Первый рабочий за час делает на 9 деталей больше, чем второй, и выполняет заказ, состоящий из 112 деталей, на 4 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
№ 2.6. Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 130 литров она заполняет на 4 минуты быстрее, чем первая труба заполняет резервуар объемом 136 литров?
№ 3.1. Слесарь может выполнить задание за 6ч, а его ученик это же задание – за 8ч. Какую часть задания они могут выполнить вместе за 1ч?
Решение:
Примем за 1 – задание.
Тогда за 1ч слесарь выполнит всего задания, а ученик -
всего задания. Работая вместе за 1ч они выполнят:
+
работы
Ответ: задания.
№ 3.2. Слесарь может выполнить задание за 6ч, а его ученик это же задание – за 8ч. Какую часть задания они могут выполнить вместе за 1ч?
Решение:
1 способ:
Примем за 1 – задание.
Тогда за 1ч слесарь выполнит всего задания, а ученик -
всего задания.
Пусть за х часов слесарь и ученик выполнят все задание, работая вместе. Учитывая, что они выполнят задание, составим и решим уравнение:
( +
х = 1
понадобится на выполнении всего задания при совместной работе
Ответ: 3 часа.
2 способ:
+
работы выполнят за 1ч, работая вместе
= 1
=
3
часа.
№ 3.3. У Ивана и Петра вместе 980 рублей. У Ивана и Никиты вместе 930 рублей, а у Петра и Никиты вместе 890 рублей. Сколько денег у каждого из них?
Решение:
(980 + 930 + 890) 2 = 2800 2 = 1400 (руб.) - у трех мальчиков вместе.
1400 – 890 = 510 (руб.) – у Ивана.
1400 – 930 = 470 (руб.) – у Петра.
1400 – 980 = 420 (руб.) у Никиты.
Ответ: 510 руб., 470 руб., 420 руб.
№ 3.4. Игорь и Паша красят забор за 20 часов. Паша и Володя красят этот же забор за 24 часа, а Володя и Игорь – за 30 часов. За сколько минут мальчики покрасят забор, работая втроем?
Решение:
Объем всей работы примем за 1.
Тогда Игорь и Паша за 1 час покрасят всего забора. Паша и Володя за 1 час -
всего забора, а Володя и Игорь -
всего забора.
= (всего забора) покрасят мальчики за 1 час, работая втроем. Значит, всю работу они выполнят за 1
= 16 часов
Ответ: за 960 минут.
№3.5. Игорь и Паша красят забор за 18 часов. Паша и Володя красят этот же забор за 20 часов, а Володя и Игорь – за 30 часов. За сколько минут мальчики покрасят забор, работая втроем?

 Получите свидетельство
Получите свидетельство Вход
Вход












 Текстовые задачи для подготовки к ОГЭ по математике (32.57 KB)
Текстовые задачи для подготовки к ОГЭ по математике (32.57 KB)
 0
0 1286
1286 38
38 Нравится
0
Нравится
0


